
|
|
Формула полной вероятностиФормула полной вероятности является обобщением теорем сложения и умножения вероятностей. Если событие А может произойти только с одним из событий
Пример. В магазин поступают электролампы с трех заводов. На первом заводе стандартные лампы составляют 90 % продукции, на втором - 95 %, на третьем - 85 %. Половина всех ламп в магазине поставлена первым заводом, 30% - вторым, 20 % - третьим. Какова вероятность купить в этом магазине стандартную лампу? Обозначим событие А - покупка стандартной лампы; оно может произойти с одним из следующих событий:
События
Полученная формула для оценки вероятности того, что событие А произошло по гипотезе Пример. Компания по страхованию делит водителей на группы: А (мало рискуют), В (средне рискуют), С (сильно рискуют). 30 % водителей относятся к группе А, 50 % – к группе В, остальные – к группе С. Вероятность попадания в аварию для водителя группы А – 0,01; группы В – 0,03; группы С – 0,1. Водитель попал в аварию. Найти вероятность, что он относится к группе С. Пусть событие Возможны следующие гипотезы:
Тогда полная вероятность для произвольного водителя попасть в аварию:
Вероятность, что это был водитель из группы С :
Повторение независимых испытаний Формула Бернулли Проведение подряд Вычислим вероятность Рассмотрим простой пример. Монету подбрасываем 4 раза, пусть событие Ц Ц Г Г ; Ц Г Ц Г ; Ц Г Г Ц ; Г Г Ц Ц ; Г Ц Ц Г ; Г Ц Г Ц . Число способов осуществить нужное нам событие совпадает с числом способов выбрать два места из четырех и равно числу сочетаний по два из четырех В общем случае, когда проводится
Полученная формула носит название формулы Бернулли. Пример. Перевозится партия из 10 деталей. Вероятность повреждения в пути отдельной детали В данном случае испытанием будет доставка отдельной детали, т.к. деталей 10, то
В некоторых задачах бывает необходимо использовать формулу Бернулли несколько по-иному. Известна вероятность Пример. Вероятность p того, что отдельный саженец приживется при посадке, равна 0,8. Сколько нужно взять саженцев, чтобы с вероятностью не меньшей 0,85 прижились, по крайней мере, 5 саженцев? Пусть число саженцев n = 5. Нас устраивает вариант, когда приживутся все 5. Вероятность этого
Эта вероятность также меньше указанной в задаче. Возьмем n = 7. Благоприятным исходом будет, если приживутся или 5 из 7 саженцев, или 6 из 7, или все 7. Вероятность этого
Следовательно, для достижения нужной вероятности нужно посадить семь саженцев. Вероятности
Преобразование данной системы приводит к двойному неравенству:
Пример 1. Вероятность изготовления изделия высшего сорта на данном предприятии равна 0,78. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 150 изделий? Наивероятнейшее число изделий Пример 2. Сколько раз нужно подбросить игральную кость, чтобы наивероятнейшее число выпадений тройки было равно 55? В данной задаче p = 1/6 и должно выполняться двойное неравенство
Это неравенство можно заменить системой:
3.2. Приближение формулы Бернулли при больших Вычисление вероятностей по формуле Бернулли, несложное при небольших
Пример. Установлено, что иммунитет против туберкулеза приобретается после прививки в 94 % случаев. Какова вероятность, что среди 100000 привитых граждан 5800 человек не защищены от болезни? В этой задаче
Поскольку вычисление факториалов в данной формуле весьма затруднительно, попробуем использовать приближение формулы Бернулли:
Однако и этой формулой бывает не всегда удобно пользоваться. Неудобство возникает, если нужно вычислить сумму большого числа вероятностей типа
что, конечно, не вызывает восторга. В подобных случаях пользуются еще одним приближением, полученным Муавром (локальная теорема Муавра):
Значения вероятности по этой формуле можно вычислить и непосредственно на калькуляторе, а можно и с помощью таблиц функции
согласно соотношению Для вычисления суммы вероятностей ее заменяют интегралом (интегральная теорема Муавра):
Для стоящей под интегралом функции первообразная не существует в аналитическом виде, поэтому пользуются табулированной (т.е. заданной в виде таблицы) функцией
Тогда
Таким образом: Пример. Вычислим с помощью функции Ф(
При вычислении использовано свойство: Ф(– 3.3. Приближение формулы Бернулли при больших Рассмотрим теперь случай когда
сокращая общие множители в
Т.к.
Эта формула для вычисления вероятности того, что при повторении Пример. В страховой компании застраховано 10000 клиентов, каждый из которых вносит в начале года 12 долларов. В случае смерти клиента (вероятность которой в течение года равна 0,006) компания выплачивает родственникам 1000 долларов. Какова вероятность, что фирма получит доход в размере 70000 долларов? Считая, что доход – это разница между суммарным взносом в 120000 долларов и выплатами по случаю смерти, посчитываем, что нужный доход получится, если в течение года умрет 50 клиентов. Значит, Случайные величины 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , образующих полную группу, то его вероятность можно вычислить следующим образом:
, образующих полную группу, то его вероятность можно вычислить следующим образом: .
. - лампа изготовлена первым заводом;
- лампа изготовлена первым заводом; - лампа изготовлена вторым заводом;
- лампа изготовлена вторым заводом; - лампа изготовлена третьим заводом.
- лампа изготовлена третьим заводом.
 , с которыми может наступить событие А, носят название гипотез. Оценить вероятность той или иной гипотезы, если событие А произошло, можно следующим образом: из полной вероятности берут ее часть, связанную гипотезой
, с которыми может наступить событие А, носят название гипотез. Оценить вероятность той или иной гипотезы, если событие А произошло, можно следующим образом: из полной вероятности берут ее часть, связанную гипотезой  .
.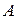 - попадание произвольно взятого водителя в аварию.
- попадание произвольно взятого водителя в аварию. .
. .
.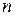 опытов (испытаний), в каждом из которых событие А может осуществиться с вероятностью p, не зависящей от результатов предыдущих испытаний, называется повторением (схемой) независимых испытаний.
опытов (испытаний), в каждом из которых событие А может осуществиться с вероятностью p, не зависящей от результатов предыдущих испытаний, называется повторением (схемой) независимых испытаний.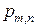 события
события  , состоящего в том, что в серии из
, состоящего в том, что в серии из 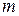 раз. Событие
раз. Событие  событий
событий  (противоположных
(противоположных  может осуществиться различными способами.
может осуществиться различными способами.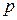 = 0,5). Событие
= 0,5). Событие  (цифра выпала 2 раза из 4-х) может произойти следующими способами:
(цифра выпала 2 раза из 4-х) может произойти следующими способами: .
.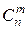 . Вероятность осуществления каждого способа равна
. Вероятность осуществления каждого способа равна  , события, соответствующие разным способам, несовместны, поэтому вероятность того, что в серии из
, события, соответствующие разным способам, несовместны, поэтому вероятность того, что в серии из  .
.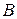 – повреждение не более двух деталей – состоит либо в благополучной доставке всех деталей (0 деталей повреждено,
– повреждение не более двух деталей – состоит либо в благополучной доставке всех деталей (0 деталей повреждено,  ;
; .
. , с которой в серии из
, с которой в серии из  раз. Нужно установить, каково должно быть число опытов
раз. Нужно установить, каково должно быть число опытов 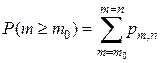 до тех пор, пока величина
до тех пор, пока величина  не достигнет
не достигнет  . Как видно, она недостаточна. Возьмем n = 6. Походящим будет случай, когда приживутся или 5 из 6 саженцев, или все 6. Вероятность этого:
. Как видно, она недостаточна. Возьмем n = 6. Походящим будет случай, когда приживутся или 5 из 6 саженцев, или все 6. Вероятность этого: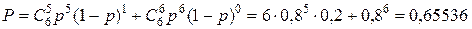 .
.
 имеет наибольшее значение, называется наивероятнейшим числом наступлений события. Его можно определить из системы неравенств:
имеет наибольшее значение, называется наивероятнейшим числом наступлений события. Его можно определить из системы неравенств:
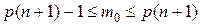 .
. или
или  . Целым числом, удовлетворяющим данному неравенству, будет
. Целым числом, удовлетворяющим данному неравенству, будет 

 .
.
 .
.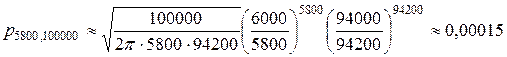 .
. ,
, .
.
 , где
, где  .
. .
. .
. , где
, где ,
,  .
. .
. ) вероятность того, что после проведения вакцинации от 5800 до 6200 граждан останутся без иммунитета.
) вероятность того, что после проведения вакцинации от 5800 до 6200 граждан останутся без иммунитета.
 .
. , получим
, получим
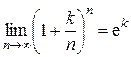 заменить
заменить  . Окончательно получим
. Окончательно получим .
. .
.