
|
|
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ДОВЕРИТЕЛЬНЫЕ ВЕРОЯТНОСТИТеоремы 1 и 2 хотя и являются общими, т. е. сформулированы при достаточно широких предположениях, они не дают возможности установить, насколько близки оценки к оцениваемым параметрам. Из факта, что —оценки являются состоятельными, следует только то, что при увеличении объема выборки значение P(|θ* – θ| < δ), δ < 0, приближается к 1. Возникают следующие вопросы. 1) Каким должен быть объем выборки п, чтобы заданная точность 2) Какова точность оценки, если объем выборки известен и вероятность безошибочности вывода задана? 3) Какова вероятность того, что при заданном объеме выборки будет обеспечена заданная точность оценки? Введем несколько новых определений. Определение. Вероятность γ выполнения неравенства, |θ*– θ| < δ называется доверительной вероятностью или надежностью оценки θ. Перейдем от неравенства |θ*–θ| < δ к двойному неравенству. Известно, что Так как θ (оцениваемый параметр) – число постоянное, а θ* – величина случайная, понятие доверительной вероятности сформулировать так: доверительной вероятностью γ называется вероятность того, что интервал (θ*– δ, θ*+ δ) накрывает оцениваемый параметр. Определение. Случайный интервал (θ*–δ, θ*+δ), в пределах которого с вероятностью γ находится неизвестный оцениваемый параметр, называется доверительным интервалом İ, соответствующим коэффициенту доверия γ, İ=(θ*– δ, θ*+ δ). (3) Надежность оценки γ может задаваться заранее, тогда, зная закон распределения изучаемой случайной величины, можно найти доверительный интервал İ. Решается и обратная задача, когда по заданному İ находится соответствующая надежность оценки. Пусть, например, γ = 0,95; тогда число р = 1 – у = 0,05 показывает, с какой вероятностью заключение о надежности оценки ошибочно. Число р=1–γ называется уровнем значимости. Уровень значимости задается заранее в зависимости от конкретного случая. Обычно р принимают равным 0,05; 0,01; 0,001. Выясним, как построить доверительный интервал для математического ожидания нормально распределенного признака. Было показано, что
Оценим математическое ожидание с помощью выборочной средней а по формуле (12.9.2) получаем Принимая во внимание (13.5.12), получим
Пусть известна вероятность γ. Тогда
Для удобства пользования таблицей функции Лапласа положим
Интервал
накрывает параметр а = М(Х)с вероятностью γ. В большинстве случаев среднее квадратическое отклонение σ(Х) исследуемого признака неизвестно. Поэтому вместо σ(Х)при большой выборке (n > 30) применяют исправленное выборочное среднее квадратическое отклонение s, являющееся, в свою очередь оценкой σ(X), İ = Пример.С вероятностью γ = 0,95 найти доверительный интервал для М(Х)– длины колоса ячменя сорта «Московский 121». Распределение задается таблицей, в которой' вместо интервалов изменения (хi, хi + 1) взяты числа
Решение. Выборка большая (n = 50). Имеем
Найдем точность оценки
Определим доверительные границы:
Таким образом, с надежностью γ = 0,95 математическое ожидание заключено в доверительном интервале I = (9,5; 10,3). Итак, в случае большой выборки (n > 30), когда исправленное среднее квадратическое отклонение незначительно отклоняется от среднего квадратического отклонения значения признака в генеральной совокупности, можно найти доверительный интервал. Но делать большую выборку удается не всегда и это не всегда целесообразно. Из (7) видно, что чем меньше п, тем шире доверительный интервал, т. е. I зависит от объема выборки п. Английский статистик Госсет (псевдоним Стьюдент) доказал, что в случае нормального распределения признака X в генеральной совокупности нормирования случайная величина
зависит только от объема выборки. Была найдена функция распределения случайной величины Т и вероятность P(T < tγ), tγ – точность оценки. Функция, определяемая равенством s (n, tγ) = P(|T| < tγ) = γ (9) названа t-распределением Стьюдента с п – 1 степенями свободы. Формула (9) связывает случайную величину Т, доверительный интервал İ и доверительную вероятность γ. Зная две из них, можно найти третью. Учитывая (8), имеем
Неравенство в левой части (13.7.10) заменим равносильным ему неравенством
или
где tγ=t(γ,n). Для функции tγ составлены таблицы (см. Приложение 5). При n>30 числа tγ и t, найденные по таблице функции Лапласа, практически совпадают. Доверительный интервал для оценки среднего квадратического отклонения σx в случае нормального распределения. Теорема.Пусть известно, что случайная величина имеет нормальное распределение. Тогда для оценки параметра σх этого закона имеет место равенство
где γ – доверительная вероятность, зависящая от объема выборки п и точности оценки β. Функция γ = Ψ (n, β) хорошо изучена. С ее помощью определяют β = β(γ,п). Для β = β(γ,п) составлены таблицы, по которым по известным п (объему выборки) и γ (доверительной вероятности) определяется β. Пример.Для оценки параметра нормально распределенной случайной величины была сделана выборка (дневной удой 50 коров) и вычислено s = 1,5. Найти доверительный интервал, накрывающий с вероятностью γ = 0,95. Решение. По таблице β(γ, п) для n = 50 и γ = 0,95 находим β = 0,21 (см. Приложение 6). В соответствии с неравенством (13) найдем границы доверительного интервала. Имеем 1,5 – 0,21·1,5 = 1,185; 1,5 + 0,21·1,5 = 1,185; 1,185 < σ < 1,185. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
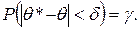 (1)
(1)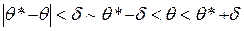 . Поэтому доверительную вероятность можно записать в виде
. Поэтому доверительную вероятность можно записать в виде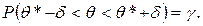 (2)
(2)
 учитывая, что
учитывая, что 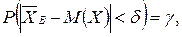 (4)
(4)
 (5)
(5)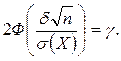
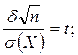 тогда
тогда 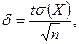 а
а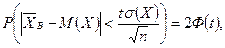
 (6)
(6)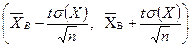 (7)
(7)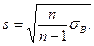 доверительный интервал будет иметь вид
доверительный интервал будет иметь вид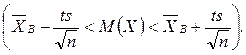
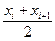 , см. Считать, что случайная величина X подчинена нормальному распределению.
, см. Считать, что случайная величина X подчинена нормальному распределению.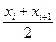

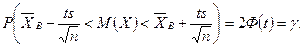
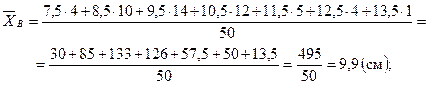

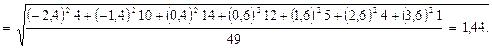

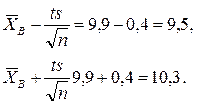
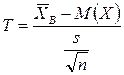 (8)
(8) (10)
(10) . В результате получим
. В результате получим
 (11)
(11)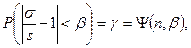 (12)
(12)