|
|
Графо-аналитический способДля определения силы давления на плоскую стенку P нужно построить эпюру гидростатического давления. Тогда сила давления будет равна площади F, умноженной на ширину стенки b: P = F b (н). (10) Формула справедлива в том случае, если ширина стенки или затвора не меняется (b = const) с изменением глубины h. Если в формулу (10) подставить вместо F площадь эпюры манометрического давления, то получим силу манометрического давления P, а если площадь эпюры полного гидростатического давления, то получим силу Pполн. Для нахождения центра давления нужно определить центр тяжести эпюры, из полученного центра провести линию, перпендикулярную к рассматриваемой поверхности до пересечения с ней, и измерить расстояние от этой точки до свободной поверхности. Это расстояние и даст расстояние до центра давления. Задача 18. Определить полное гидростатическое давление (р') на дно круглого резервуара d = 1 м, а также силу давления на дно (Pполн) в двух предположениях: 1) резервуар наполнен водой; 2) резервуар наполнен бензином ( γб = 6867 н/м3). Глубина наполнения в обоих случаях одинакова и равна h = 0,9 м. Сосуд сверху открыт и давление на свободной поверхности равно атмосферному. Решение: 1) р' = рат + γ h = 98100 + 9810 · 0,9 = 106929 (н/м2); Pполн = (рат + γ h)· ω = р' ω = р' 2) р' = рат + γ h = 98100 + 6867 · 0,9 = 104280 (н/м2); Pполн = (рат + γ h)· ω = р' ω = р' Ответ: 1) р' = 106929 (н/м2), Pполн = 83939 (н/м2); 2) р' = 104280 (н/м2); Pполн = 81860 (н/м2). Задача 19. Для условий предыдущей задачи определить манометрическое давление (р) и силу манометрического давления на дно резервуара (P). Задача 20. Определить силу манометрического давления (Р) на дно сосудов а, б, в и г (рис. 10), наполненных водой. Высота столба h = 60 см, а h1 = 50 см и h2 = 40 см. Площадь дна сосудов ω = 1250 см2, а площадь сечения ω1 = 12,5 см2. Найти силу (G), передаваемую в каждом случае на пол, пренебрегая весом сосудов. Почему сила давления на дно не всегда совпадает с весом воды, заключенной в сосуде? Объясните гидростатический парадокс, определив силу манометрического давления (Рф), воспринимаемую фасонной частью АВСD (б) или АВ (схемы в и г).
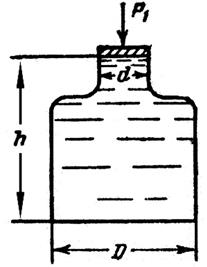
Рис. 10 Задача 21. Определить силу манометрического давления на дно сосуда (Р), если сила P1, действующая на поршень, равна 44 н (рис. 11). Диаметр d = 12 см, глубина воды в сосуде h = 40 см, диаметр дна сосуда D = 35 см.
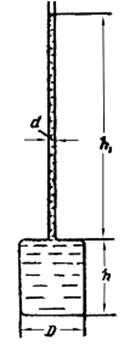
Рис. 11 Задача 22. Стальная бочка диаметром D = 0,60 м, высотой h = 0,9 м заполнена водой. Определить: 1) Силу манометрического давления P1 на дно бочки, силу G1, передаваемую на пол, если масса пустой бочки равна 35 кг. 2) Силу манометрического давления P2 на дно бочки, если в крышке просверлить отверстие и к нему приварить вертикальную трубку диаметром d = 2 см, длиной h1 = 15 м, которую заполнить водой (рис. 12). 3) Силу G2, передаваемую на пол во втором случае, пренебрегая весом трубки. 4) Силу манометрического давления P3 на верхнюю крышку. 5) Что воспринимает силу давления, равную разности между силой манометрического давления на дно P2 и силой веса жидкости в бочке?
Рис. 12 Решение: 1) Сила манометрического давления P1 на дно бочки равна Р1 = γ hω= γ h Вес бочки в ньютонах: Gбоч = g m = 9,81 · 35 = 343,35 (н). Сила G1, передаваемая на пол равна G1 = Р1+ Gбоч = 2495 + 343,35 = 2838 (н). 2) Р2 = γ (h + h1) ω = 9810 · 15,9 · 0,2826 = 44079,7 (н). 3) G2 = γ h1 ω1 + G1 = 9810 · 15 · 0,000314 + 2838 = 2884 (н). 4) Р3 = Р2 -Р1= 44079,7 – 2495 = 41584,7 (н). 5) Верхняя крышка воспринимает силу давления, равную разности между силой манометрического давления на дно (P2) и силой веса жидкости в бочке (Gбоч). Сила веса жидкости – это и есть манометрическое давление на дно бочки. Ответ: 1) Р1 = 2495 (н), G1 = 2838 (н); 2) Р2 = 44079,7 (н); 3) G2 = 2884 (н); 4) Р3 = 41584,7 (н); 5) Верхняя крышка воспринимает силу давления, равную разности между силой манометрического давления на дно (P2) и силой веса жидкости в бочке (Gбоч). Задача 23. Какую силу (P2) нужно приложить к большему поршню, чтобы система находилась в равновесии (рис. 13)? Сила, приложенная к меньшему поршню, P1 = 147 н. Диаметр большего поршня D = 300 мм, меньшего d = 50 мм. Разность уровней h = 30 см. Трубки заполнены водой. Весом поршней пренебречь. Сколько процентов составляет сила давления столба воды (p · ω2) от найденной силы P2?
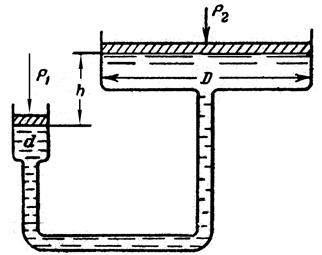
Рис. 13 Задача 24. Труба диаметром D = 400 мм соединена с трубой диаметром d = 50 мм, как показано на чертеже (рис. 14). Высота столба воды h = 80 см. В трубах имеются поршни. Какое усилие (P2) нужно приложить на поршни А и В, чтобы система находилась в равновесии, если на поршень С действует сила P1 = 98,1 н. Решение:
Ответ: Р2 = 7264 (н).
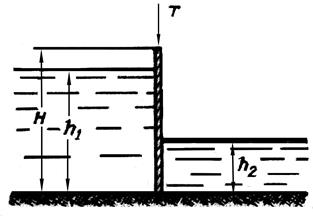
Рис. 14 Задача 25. Определить силу давления (P) на плоский прямоугольный затвор и центр давления (l∂). Глубина воды в верхнем бьефе h1 = 3 м, а в нижнем h2 = 1,2 м. Ширина затвора b = 4 м, высота H = 3,5 м (рис. 15). Расчет произвести аналитическим и графо-аналитическим способами. Найти начальное подъемное усилие (Т), если толщина затвора t = 0,08 м, удельный вес материала, из которого изготовлен затвор γд = 11800 н/м3, а коэффициент трения затвора о пазы f = 0,5.
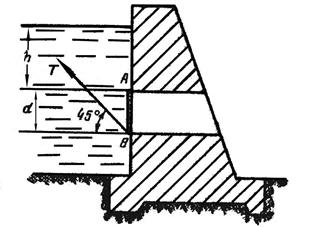
Рис. 15 Задача 26. Найти силу (Т), с которой нужно тянуть трос, прикрепленный к нижней кромке плоского круглого затвора диаметром d = 2 м, закрывающего отверстие трубы. Затвор может вращаться вокруг шарнира А. Глубина воды над верхней кромкой затвора h = 3 м (рис. 16). Трос направлен под углом 45 градусов к горизонту. Решение: 1) Найдем силу манометрического давления Р = γ hц.т. ω = γ π r2 (h + r) = 9810 · 3,14 · 12 · 4 = 123214 (н), где hц.т = h + r = 1 + 3 = 4 (м); ω = π r2 = 3,14 · 12 =3,14 (м2). l∂ = lц.т + Jо / ω lц.т , (9) 2) Найдем расстояние от свободной поверхности до центра давления (считая по наклону стенки) по формуле (9) l∂ = lц.т + Jо / ω lц.т . При круглой пластине (α = 900, при h0 > 0) Jо = π d4 / 64. Подставим в формулу (9) hц.т и Jо. Получим 3) Составим уравнение равновесия относительно шарнира А: T d sin 450 – P (lд – h) = 0 4) Выразим отсюда силу (Т) с которой нужно тянуть трос где sin 450 = Ответ: Сила с которой надо тянуть трос равна Т= 92400 н.
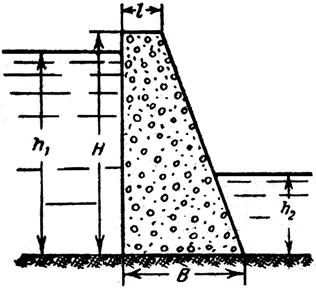
Рис. 16 Задача 27. Гравитационная плотина, изображенная на рис. 17, запроектирована таким образом, что отношение удерживающего момента к опрокидывающему равно 2. Определить размеры плотины понизу (В), если глубина воды перед плотиной h1 = 15 м, ниже плотины h2 = 6 м. Высота плотины H = 16,5 м, ширина поверху L = 3 м. Удельный вес бетона γб = 23544 н/м3. Чему равнялась бы ширина плотины понизу, если при расчете пренебречь наличием воды ниже плотины?
Рис. 17 Приложение 2
Продолжение приложения 2
3. СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ
Ниже рассмотрим только простейший случай криволинейной поверхности – цилиндрическую поверхность, которая встречается наиболее часто. Обозначим через Pх и Pу горизонтальную и вертикальную составляющие силы гидростатического давления P, действующего со стороны жидкости на цилиндрическую поверхность. 1. Горизонтальная составляющаяPх искомой силы P равна силе давления жидкости на плоскую вертикальную прямоугольную фигуру, представляющую собой проекцию рассматриваемой цилиндрической поверхности на вертикальную плоскость. 2. Вертикальная составляющаяPу искомой силы P равна взятому со знаком минус весу воображаемого жидкого тела. Это воображаемое жидкое тело называется телом давления. Обозначив вес тела давления через Go, получаем P0 = – Go. (11) Если рассматриваемая цилиндрическая поверхность со стороны тела давления не смачивается жидкостью, то имеем отрицательное тело давления; в противном случае – положительное тело давления. В случае, когда жидкость находится над цилиндрической поверхностью вертикальная составляющая Pу будет равна Pу = + Go. (12) Поперечное сечение тела давления (отрицательного или положительного) представляет собой фигуру, заключенную между указанными вертикалями, самой цилиндрической поверхностью и горизонтом жидкости (или его продолжением). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
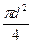 = 106929 · 0,785 = 83939 (н/м2).
= 106929 · 0,785 = 83939 (н/м2).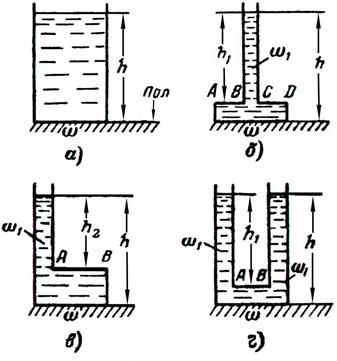
 ;
;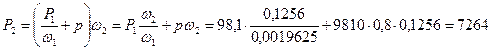 (н).
(н).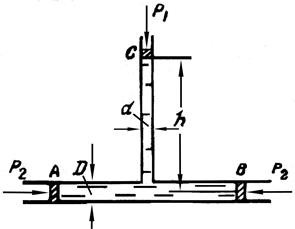
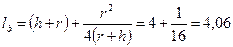 (м).
(м).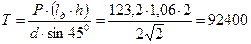 (н),
(н),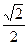 .
.