|
|
Система Пирамидального Умножения
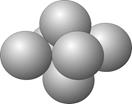
Пирамидальная система умножения изначально охватывает трехмерные производные (длина, ширина, высота), соответственно двухмерного (плоскостного) умножения не содержит. При пирамидальном умножении множитель указывает на количество мерных точек (количество рядов) по всем трем направлениям в пирамидальной структуре. Изначальной структурой данного умножения является Малая Пирамида:

x & 2 \ x2 = 5
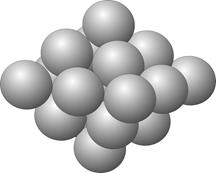
  x & 3 \ x3 = 14 x & 3 \ x3 = 14
При подсчете количества точек в пирамидах следует учесть тот факт, что их «горизонтальные ряды» есть не что иное, как Ровны.
xn = Yn + Yn-1 + Yn-2 + …+ Y2 + 1
или (если известен результат предыдущего умножения пирамида жды):
xn = xn-1 + Yn
Призменная система умножения
Данная система умножения, так же как и Пирамидальная изначально является трехмерной. Существуют две системы Призменного умножения, построенные на применении следующих структур:
1) Малая Призма, обозначаемая знаком - u
2) Ровная Призма, обозначаемая знаком - r
Умножение Малой Призмы При вычислении Малой Призмы следует учесть, что:
полной разверткой указывается количество рядов в Призме и данное число всегда нечетное,
сокращенной разверткой указывается количество визуальных основ,
  u2 \ u & 3 = 5 u2 \ u & 3 = 5

При умножении Малой Призмы результат есть сумма Малой Триады в основании и двух Трехмерных Триад.
Соответственно, результат можно вычислить по следующей формуле:
un \ u & (n * 2 - 1) = zn + en-1 + en-1 или (зная результат предыдущей Малой призма жды)
un \ u & (n * 2 - 1) = un-1 + zn-1 + zn
Умножение Ровной Призмы При вычислении Ровной Призмы, так же как и при Малой:
полной разверткой указывается количество рядов в Призме и данное число всегда нечетное,
сокращенной разверткой указывается количество визуальных основ,
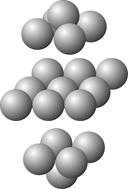
 r2 \ r & 3 = 6 r2 \ r & 3 = 6
При Ровно Призменном умножении малая (двухмерная) Ровна суммируется с двумя Пирамидами, имеющими множители на единицу меньше.
Формулы вычисления «Ровно призма жды»:
rn = r & (n * 2 – 1) = yn + xn-1 + xn-1
или (опять же зная результат предыдущей Ровно призма жды):
rn = r & (n * 2 – 1) = rn-1 + yn + yn
Пядевая система мер
Пядевая система мер существовала еще до привязки ее к человеческому организму. Основу данной системы мер составляет пядь: ç p
p (пядь) равна 17,78 см, что примерно составляет расстояние от конца большого пальца до конца указательного при их разведения в стороны. Для обозначения мерности над знаками ставится специальный указатель, означающий, что данное обозначение определяет длину чего-либо, например пядь указывающая на длину изображается следующим образом: q Для обозначения простой цифирности также применяется специальный знак, например числовое обозначение «тьмы» (10.000) выглядит следующим образом: U В пядевой системе мер существуют следующие основные группы величин: - основные малые меры; - основные средние меры; - основные большие меры.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Знак Пирамидального умножения - x. Данная система умножения используется для вычисления количественных объемов. В древние времена ее использовали при строительстве пирамид, храмов декуратов и капищ.
Знак Пирамидального умножения - x. Данная система умножения используется для вычисления количественных объемов. В древние времена ее использовали при строительстве пирамид, храмов декуратов и капищ.





 Соответственно, формула Пирамидального умножения выводится через умножение «Ровно на» :
Соответственно, формула Пирамидального умножения выводится через умножение «Ровно на» :




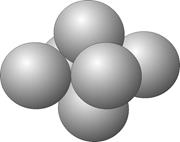
 например - u & 3
например - u & 3






 например - r & 3
например - r & 3 например - r2
например - r2