
|
|
Триадная система умножения.
Триадная система умножения при вычислении использует структуры малой и трехмерной триад:
- малая триада (основание - 3)
-
Двухмерное триадное умножение.
Малая триада при данном умножении указывает на структуру, построение формы которой используется при вычислении. При двухмерных триадных вычислениях, в качестве первого множителя, используется знак двухмерной триады - Zили z. Второй множитель указывает на количество рядов в триаде. Результатом же является количество точек в получившейся триаде.


Z * 6 \ Z6 = 21
Z * 8 \ Z8 = 32 Z * 9 \ Z9 = 41 Z * 10 \ Z10 = 51 Z * 11 \ Z11 = 66 Z * 12 \ Z12 = 78 Z * 13 \ Z13 = 91 Z * 14 \ Z14 = 105 Z * 15 \ Z15 = 120 Z * 16 \ Z16 = 136
Трехмерное триадное умножение.
При трехмерных триадных вычислениях, в качестве первого множителя, используется знак объемной триады - eили знак z, если задано трехмерное умножение знаком ЖДЫ (&). Второй множитель указывает на количество рядов в триаде. Результатом является количество точек в получившейся триаде.
  z & 3 \ e2 = 10 z & 3 \ e2 = 10
en ≡ en-1 + Zn
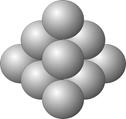
Дело в том, что трехмерная триада состоит из соединенных между собой плоскостями малыми триадами, у которых длины сторон увеличиваются на единицу по порядку возрастания номеров рядов в трехмерной триаде (если рядом номер один считать самый верхний ряд). Например структура трехмерной триады сформированная умножением триадно жды три ( e3 ) состоит из следующих малых триад:

Ряд №1 = 1
Ряд №2 - Z2 = 3
Ряд №3 - Z3 = 6
Триадно жды четыре получается путем «добавления снизу» еще одной малой триады, длина стороны которой будет уже равна четырем, т.е.:
Если при вычислении таблиц трехмерного триадного умножения не брать в расчет таблицы двухмерного умножения, то путем нехитрых вычислений можно получить еще одну формулу:
en ≡ en-1 - en-2 + en-1 + n
Например:
e5 ≡ e5-1 - e5-2 + e5-1 + 5 = e4 - e3 + e4 + 5 = 20 – 10 + 20 + 5 = 35
Ровная система умножения
Данная система так называется от понятия «Ровна» т.е. равномерная структура, где количество точек по любым направлениям равны между собой. Существуют следующие виды Ровны: 1)
 Малая Ровна Малая Ровна
2)
 Трехмерная Ровна Трехмерная Ровна
Умножение Малой Ровны
Результат данного умножения определяется суммой точек в малой Ровне, причем второй множитель показывает количество рядов точек в обеих сторонах Ровны.
 y * 2 \ Y2 = 4 y * 2 \ Y2 = 4
y * 4 \ Y4 = 16
Явно видно, что результат умножения «ровно на …» получается путем плоскостного умножения второго множителя на самого себя, т.е.:
Yn \ n * n
Умножение Трехмерной Ровны
 y & 2 \ E2 = 8 y & 2 \ E2 = 8
 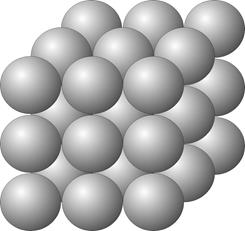 y & 3 \ E3 = 27 y & 3 \ E3 = 27
y & 4 \ E4 = 64
Результат умножения «ровно ЖДЫ …» получается путем плоскостного умножения второго множителя на самого себя со степенью повторений умножения равного самому себе, т.е.:
или, говоря языком «стандартной математики», результат возведения в куб ( n3 ) множителя ровно жды и будет результатом данного умножения.
Пример решения арифметического действия:
т.к. после ровно жды не указан какой-либо множитель, то подразумевается изначальная структура Трехмерной Ровны т.е. E2.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

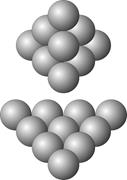
 трехмерная триада (основание - 4)
трехмерная триада (основание - 4)




 Z * 2 \ Z2 = 3
Z * 2 \ Z2 = 3





 Z * 3 \ Z3 = 6
Z * 3 \ Z3 = 6
 Z * 7 \ Z7 = 28
Z * 7 \ Z7 = 28
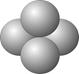

 z & 2 \ e2 = 4
z & 2 \ e2 = 4



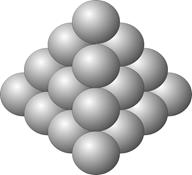
 В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:
В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:
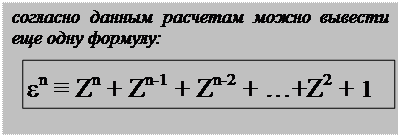













 Результат этого умножения определяется суммой точек в трехмерной Ровне. Второй множитель показывает количество рядов точек во всех трех сторонах Ровны.
Результат этого умножения определяется суммой точек в трехмерной Ровне. Второй множитель показывает количество рядов точек во всех трех сторонах Ровны.
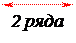




 En \ n * |n|n
En \ n * |n|n

 Y * 3 + E = 9 + E = 9 + 8 = 17
Y * 3 + E = 9 + E = 9 + 8 = 17