
|
|
Структуры различных мерностей с основанием три.Системы умножения и их структурные проекции. Гармоничные фигуры и их проекции.
Гармоничная фигура одномерного пространства.
В одномерном пространстве любая фигура (структура) будет иметь две опорные точки. Данное утверждение легко визуально проверить – достаточно нарисовать на поверхности листа бумаги (двухмерного пространства) любую фигуру, затем повернуть лист ребром к наблюдателю. Если толщиной листа пренебречь, то мы получим одномерное пространство с нарисованной нами фигурой, которая будет выглядеть как отрезок. Любой отрезок будет всегда иметь две опорные точки. Данное утверждение можно записать следующим образом:
| a |1 = 2
Иначе говоря, для определения какой-либо структуры спроектированной на одномерное пространство необходимо определить две ее опорные точки.
Гармоничная фигура двухмерного пространства.
Для получения гармоничной структуры двухмерного пространства необходимо провести перпендикуляр к одномерной фигуре (проекции структуры на одномерном пространстве) на длину самой фигуры, т.е. одномерная фигура «двигается» на длину самой себя по вектору являющемся перпендикуляром к ней. Оставленный при движении «след» и будет являться гармоничной фигурой двухмерного пространства.
Получившаяся гармоничная фигура двухмерного пространства будет являться квадратом и соответственно иметь четыре опорные точки т.е.:
| а |2 = 4
Гармоничная фигура трехмерного пространства. При увеличении мерности пространства на единицу гармоничная фигура получается путем проекции гармоничной фигуры предыдущей мерности на ее же длину по вектору являющимся перпендикуляром к ней и к векторам измерения предыдущей мерности, т.е.:
Согласно данному правилу, для получения гармоничной фигуры трехмерного пространства необходимо осуществить проекцию (движение) гармоничной фигуры двухмерного пространства на длину самой себя по вектору являющемуся перпендикуляром к векторам измерения мерности двухмерного пространства, т.е.:
Получившийся при проекции объемный след будет являться гармоничной фигурой трехмерного пространства, т.е. кубом и иметь уже восемь опорных точек.
Гармоничная фигура четырехмерного пространства.
Аналогичным образом получаются гармоничные фигуры следующих измерений. К примеру, что бы получить гармоничную фигуру четырехмерного пространства необходимо осуществить проекцию гармоничной фигуры трехмерного пространства – куба на длину самого куба по вектору являющимся перпендикуляром к векторам измерений трехмерного пространства т.е.:
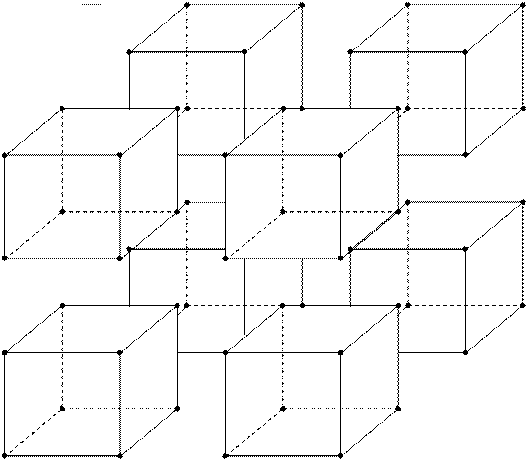
На плоскости это можно изобразить следующим образом (для удобства восприятия углы отмечены цифрами):
Отобразив куб таким образом, мы фактически осуществили сдвиг его по времени и получили гармоничную четырехмерную фигуру, которая имеет шестнадцать опорных точек, т.е.:
По данной аналогии легко выстраиваются гармоничные фигуры следующих порядков мерности их пространств.
Гармоничная фигура пятимерного пространства.
Гармоничная фигура шестимерного пространства.
Таблица соответствий гармоничных фигур разномерных пространств с количеством их опорных точек.
Триадные системы.
Структуры различных мерностей с основанием три.
Структура, в основании которой лежит число три, имеет три опорные точки в двухмерном пространстве и является равносторонним треугольником:
| 3 |2 = 3
Для получения трехмерной структуры необходимо спроецировать двухмерную структуру (треугольник) по всем ее сторонам:
Что бы получить четырехмерную структуру необходимо заставить трехмерную структуру вращаться во времени, т.е. осуществить ее проекцию во времени:
| 3 |4 = 5
Получение пятимерной структуры осуществляется через проекцию четырехмерной в пространстве (для удобства восприятия углы обозначены цифрами):
       | 3 |5 = 9 (точка №1 является общей для обоих проекций) | 3 |5 = 9 (точка №1 является общей для обоих проекций)
Получение структур в следующих по мерности пространств достигается путем проекции структур предыдущих мерностей через общие точки, например - шестимерная структура.
Для получения семимерной структуры необходимо к шестимерной «прицепить» точно такую же шестимерную структуру так, что бы между ними были четыре общие точки:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 мерность пространства, которым ограничена структура
мерность пространства, которым ограничена структура какая-либо структура
какая-либо структура

 | a |2 ≡| a |1| a |1 ≡4
| a |2 ≡| a |1| a |1 ≡4

 | a |N ≡| a |N-1 | a |N-1
| a |N ≡| a |N-1 | a |N-1 | a |3 =| a |2 | a |2
| a |3 =| a |2 | a |2


 | a |3 ≡| a |2 | a |2 ≡8
| a |3 ≡| a |2 | a |2 ≡8 | a |4 =| a |3 | a |3
| a |4 =| a |3 | a |3 
 | a |5 ≡| a |4 | a |4 ≡32
| a |5 ≡| a |4 | a |4 ≡32

 | a |2
| a |2
 | a |7
| a |7



 Данная структура имеет уже четыре опорные точки, т.е.:
Данная структура имеет уже четыре опорные точки, т.е.:
 | 3 |3 = 4
| 3 |3 = 4



 Как видно получившаяся фигура имеет пять опорных точек, следовательно:
Как видно получившаяся фигура имеет пять опорных точек, следовательно: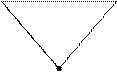

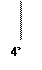








 | 3 |6 ≡| 3 |5 | 3 |5 - 2 (общие точки) ≡16
| 3 |6 ≡| 3 |5 | 3 |5 - 2 (общие точки) ≡16
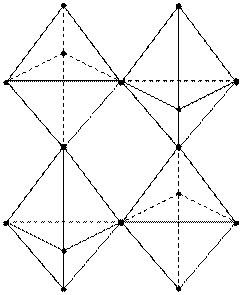



 | 3 |7 ≡ | 3 |6 | 3 |6 ≡16 + 16 – 4 (общ.точки) ≡28
| 3 |7 ≡ | 3 |6 | 3 |6 ≡16 + 16 – 4 (общ.точки) ≡28