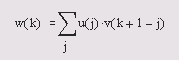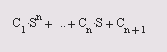|
|
Минимизация функции одной переменнойЕще одна важная задача численных методов — поиск минимума функции f(x) в некотором интервале изменения х — от х 1 до х 2 . Если нужно найти максимум такой функции, то достаточно поставить знак «минус» перед функцией. Для решения этой задачи используется следующая функция: [X.fval.exitflag,output] = fminbnd(@fun.x1,x2.options, p1,p2,...) ?????? · fminbnd(@fun,xl,x2) — возвращает значение х, которое является локальным минимумом функции fun(x) на интервале xl<x<x2; · fminbnd(@fun,xl,x2.options) — сходна с описанной выше формой функции, но использует параметры to!X, maxfuneval, maxiter, display из вектора options, предварительно установленные при помощи команды optimset (смотрите описание lsqnonneg); · fminbnd(@fun,xl.x2,options.P1.P2...) — сходна с описанной выше, но передает в целевую функцию дополнительные аргументы: Р1, Р2..... Если требуется использовать параметры вычислений по умолчанию, то вместо options перед P1, Р2 необходимо ввести [ ] (пустой массив); · [x.fval] = fminbnd(...) — дополнительно возвращает значение целевой функции fval в точке минимума; · [x.fval .exitflag] = fminbndL.) —дополнительно возвращает параметр exitflag, равный 1, если функция сошлась с использованием options.tolX, и 0, если достигнуто максимальное число итераций options.maxiter. В этих представлениях используются следующие обозначения: xl. х2 — интервал, на котором ищется минимум функции; Р1.Р2... — дополнительные, помимо х, передаваемые в функцию аргументы; fun — строка, содержащая название функции, которая будет минимизирована; options — вектор параметров вычислений. В зависимости от формы задания функции fminbnd вычисление минимума выполняется известными методами золотого сечения или параболической интерполяции. Пример: » %options=optimset('tolX',1.е-10): %[x]=fminbnd(@cos.3,4,options) % Так лучше: >>[x, options]=fmin(‘cos’,3,4,[0,1.e-10]) х = 3.1416 options= 1.0e+002
Численное интегрирование Численное интегрирование традиционно является одной из важнейших сфер применения математического аппарата. В данном разделе приводятся функции для численного интегрирования различными методами. Численное интегрирование заключается в приближенном вычислении определенного интеграла вида одним из многочисленных численных методов, для вычисления неопределенного интеграла по рекурсивному алгоритму усредняются значения b=a+dn, где d — предельно малая величина.
Метод трапеций Приведенные ниже функции выполняют численное интегрирование методом трапеций и методом трапеций с накоплением. · trapz(Y) — возвращает определенный интеграл, используя интегрирование методом трапеций с единичным шагом между отсчетами. Если Y — вектор, то trapz(Y) возвращает интеграл элементов вектора Y, если Y — матрица, то trapz(Y) возвращает вектор-строку, содержащую интегралы каждого столбца этой матрицы; · trapz(X.Y) — возвращает интеграл от функции Y по переменной X, используя метод трапеций (пределы интегрирования в этом случае задаются начальным и конечным элементами вектора X); · trapz(...,dim) — возвращает интеграл по строкам или по столбцам для входной матрицы в зависимости от значения переменной dim. Примеры: »Y=[1.2.3.4] Y = 1 2 3 4 » trapz(y) ans = 7.5000 » X=0:pi/70:pi/2; » Y=cos(X); » Z = trapz(Y) Z = 22.2780 · cumtrapz(Y) — возвращает численное значение определенного интеграла для функции, заданной ординатами в векторе или матрице Y с шагом интегрирования, равным единице (интегрирование методом трапеций с накоплением). В случае когда шаг отличен от единицы, но постоянен, вычисленный интеграл достаточно умножить на величину шага. Для векторов эта функция возвращает вектор, содержащий результат интегрирования с накоплением элементов вектора Y. Для матриц — возвращает матрицу того же размера, что и Y, содержащую результаты интегрирования с накоплением для каждого столбца матрицы Y; · cumtrapz(X, Y) — выполняет интегрирование с накоплением от Y по переменной X, используя метод трапеций. X и Y должны быть векторами одной и той же длины или X должен быть вектором-столбцом, a Y — матрицей; · cumtrapz(...,dim) — выполняет интегрирование с накоплением элементов по размерности, точно определенной скаляром dim. Длина вектора X должна быть равна size(Y.dim). Примеры: » cumtrapz(y) ans= 0 1.5000 4.0000 7.5000 » Y=magic(4) Y = 162 3 13 5 11 10 8 97 6 12 4 14 15 1 » Z= cumtrapz(Y.l) Z = 0 0 0 0 10.5000 6.5000 6.5000 10.5000 17.5000 15.500014.500020.5000 24.0000 26.000025.000027.0000
Численное интегрирование методом квадратур Приведенные ниже функции осуществляют интегрирование и двойное интегрирование, используя квадратурную формулу Симпсона или метод Гаусса-Лобатто. Квадратура — численный метод нахождения площади под графиком функции/(т), т. е. вычисление определенного интеграла вида
В приведенных ниже формулах подынтегральное выражение fun обычно задается в форме дескриптора функции, поэтому с дидактическими целями используем нотацию @fun. Функции quad и quadl используют два различных алгоритма квадратуры для вычисления определенного интеграла. Функция quad выполняет интегрирование по методу низкого порядка, используя рекурсивное правило Симпсона [4, 40]. Но она может быть более эффективной при негладких подынтегральных функциях или при низкой требуемой точности вычислений. Алгоритм quad в MATLAB 6 изменен по сравнению с предшествовавшими версиями, точность по умолчанию по сравнению с версиями 5.3х повышена в 1000 раз (с 10- 3 до 10- 6 ). Новая функция quadl (квадратура Лобатто) использует адаптивное правило квадратуры Гаусса— Лобатто очень высокого порядка. Устаревшая функция quads выполняла интегрирование, используя квадратурные формулы Ньютона—Котеса 8-го порядка [40]. Достижимая точность интегрирования гладких функций в MATLAB 6 поэтому также значительно выше, чем в предшествующих версиях. · quad(@fun,a.b) — возвращает численное значение определенного интеграла от заданной функции @fun на отрезке [а Ь]. Используется значительно усовершенствованный в MATLAB 6 адаптивный метод Симпсона; · quad(@fun,a.b.tol) — возвращает численное значение определенного интеграла с заданной относительной погрешностью tol. По умолчанию to1=l.e-6. Можно также использовать вектор, состоящий из двух элементов tol =[rel_tol abs_tol], чтобы точно определить комбинацию относительной и абсолютной погрешности; · quad(@fun,a.b,tol .trace) — возвращает численное значение определенного интеграла и при значении trace, не равном нулю, строит график, показывающий ход вычисления интеграла; · quad(@fun,a,b.tol,trace,PI,P2,...) — возвращает численное значение определенного интеграла по хот подынтегральной функции fun, использует дополнительные аргументы P1, P2,..., которые напрямую передаются в подынтегральную функцию: G=fun(X.Pl,P2,...). Примеры: » quad('(exp(x)-l)',0,1,1e-5) ans = 0.7183 » q = quad(@exp,0,2,1e-4) q = 6.3891 » q = quad(@sin.0,pi,le-3) q = 2.0000 · dblquad(@fun,inmin,inmax.outmin,outmax) — вычисляет и возвращает значение двойного интеграла для подынтегральной функции fun (Inner, outer), по умолчанию используя квадратурную функцию quad. Inner — внутренняя переменная, изменяющаяся на закрытом интервале от inmin до inmax, a outer — внешняя переменная, изменяющаяся на закрытом интервале от outmin до outmax. Первый аргумент @fun — строка, описывающая подынтегральную функцию. Этс может быть либо дескриптор функции, либо объект inline (в последнем случае символ «@» в ее записи отсутствует). Обычная запись в апострофах тепер недопустима. Эта функция должна быть функцией двух переменных вид. fout=fun(inner.outer). Функция должна брать вектор inner и скаляр outer возвращать вектор fout, который является функцией, вычисленной в outer и каждом значении inner [ Функция inime('expr', 'argl',...'argn') так же создает объект, но без дескриптора, 'ехрг' — выражеши Строки 'argx' —входные аргументы. При их отсутствии по умолчанию подставляется х. Если вмест 'arg' — скаляр, то он означает количество дополнительных переменных Р. Примеры запис; g = inline(exp); g - inline('t A 2'); g = inline('sin(2*pi*f + theta)'); g = inline('sin(2*pi*f + theta)', : 'theta'); g - inline('x A Pl+P2', 2). - Примеч. ред. ]; · dblquad(@fun,inmin.inmax.outmin,oiitmax,tol .trace) — передает в функцию dblquad параметры tol и trace. Смотрите справку по функции quad для получения информации о параметрах to! и trace; · dblquad(@fun,inmin,inmax,outmin,outmax.tol .trace,order) — передает параметры tol и trace для функции quad или quadl в зависимости от значения строки order. Допустимые значения для параметра order — @quad , @quadl или имя любого определенного пользователем квадратурного метода с таким же вызовом и такими же возвращаемыми параметрами, как у функций quad и quad!. (Например, при проверке старых программ можно использовать @quad8 для большей совместимости с прежними версиями MATLAB). По умолчанию (без параметра order) вызывается @quad. поскольку подинтегральные функции могут быть негладкими. Пример: пусть m-файл integl.m описывает функцию 2*y*sin(x)+x/2*cos(y), тогда вычислить двойной интеграл от той функции можно следующим образом: » result = dblquad(@integl,pi,2*pi,0.2*pi) result = 78.9574 Работа с полиномами Полиномы (у нас их принято называть также степенными многочленами) — широко известный объект математических вычислений и обработки данных. Обычно полином записывается в виде р(х) = а п х^n + x п-1 x^n -1+ ... + а 2 x^2 + а 1 ^х + а 0 , и так обычно принято в MATLAB для п, отрицательных по умолчанию, хотя и возможны иные формы записи, например р(х) = a 1 x^n + а 2 x^n-1 + ... + а п х + а п+1 Последняя запись обычно принята в MATLAB для n, по умолчанию положительных.
Умножение и деление полиномов Ниже приведены функции, осуществляющие умножение и деление полиномов, или, что то же самое, свертку двух входных векторов, в которых находятся коэффициенты полиномов, и операцию, обратную свертке. · w = conv(u.v) — возвращает свертку векторов и и v. Алгебраически свертка — то же самое, что и произведение полиномов, чьи коэффициенты — элементы векторов и и v. Если длина вектора и равна т, а длина вектора v — п, то вектор w имеет длину т+п-1, а его k-й элемент вычисляется по следующей формуле
Пример: » f=[2.3.5.6];d=[7,8,3]:r=conv(f,d) r = 14 37 65 91 63 18 · [q,r] = deconv(v.u) —возвращает результат деления полинома v на полином u. Вектор q представляет собой частное от деления, а г — остаток от деления, так что выполняется соотношение v=conv(u,q)+r. Пример: » t=[14,37.65.91,63,18]:r=[7.8.3];[w.e]=deconv(t.r) w = 2.0000 3.0000 5.0000 6.0000 е = 1.0е-013 0 0 0.1421 -0.1421-0.2132-0.1066
Вычисление полиномов В этом разделе приведены функции вычисления коэффициентов характеристического полинома, значения полинома в точке и матричного полинома. · poly(A) — для квадратной матрицы А размера пхп возвращает вектор-строку размером n+1, элементы которой являются коэффициентами характеристического полинома det(A-sI), где I — единичная матрица, as — оператор Лапласа. Коэффициенты упорядочены по убыванию степеней. Если вектор состоит из n+1 компонентов, то ему соответствует полином вида c 1 s^n+...+c n s+c n+1 ; · poly (г) — для вектора г возвращает вектор-строку р с элементами, представляющими собой коэффициенты полинома, корнями которого являются элементы вектора г. · Функция roots(p) является обратной, ее результаты, умноженные на целое число, дают poly (r ). ???????? А = 2 3 6 3 8 6 1 7 4 » d=poly(A) d = 1.0000 -14.0000 -1.0000-40.0000 » А=[3,6.8:12.23.5:11.12.32] ?????? А = 3 6 8 1223 5 1112 32 » poly(A) ans = 1.0000 -58.0000 681.0000 818.0000 Приведенная ниже функция вычисляет корни (в том числе комплексные) для полинома вида
· roots (с) — возвращает вектор-столбец, чьи элементы являются корнями полинома с. Вектор-строка с содержит коэффициенты полинома, упорядоченные по убыванию степеней. Если C имеет n+1 компонентов, то полином, представленный этим вектором, имеет вид . Пример: » x=[7.45.12.23];d=roots(x) %????? x=[7,45,12,23]; или x=[7 45 12 23]; d = -6.2382 -0.0952+0.7195i -0.0952 -0.7195i А=[-6.2382 -0.0952 +0.71951 -0.0952 -0.71951]: B=Poly (А) В=[1.0000 6.4286 1.7145 3.2859] В*7 ans = 7.0000 45.000212.001523.0013 С погрешностью округления получили тот же вектор. · polyval (p,x) — возвращает значения полинома р, вычисленные в точках, заданных в массиве х. Полином р — вектор, элементы которого являются коэффициентами полинома в порядке уменьшения степеней, х может быть матрицей или вектором. В любом случае функция polyval вычисляет значения полинома р для каждого элемента х; · [у.delta] = polyval (p. x.S) или [у,delta] = polyval (p.x.S.mu)—использует структуру S, возвращенную функцией polyfit, и данные о среднем значении (mu(l)) и стандартном отклонении (mu(2)) генеральной совокупности для оценки пр-грешности аппроксимации (y+delta). Пример: » р=[3,0.4.3]; d=polyval(p,[2,6]) d = 35 675 · polyvalm(p.X) — вычисляет значения полинома для матрицы. Это эквивалентно подстановке матрицы X в полином р. Полином р — вектор, чьи элементы являются коэффициентами полинома в порядке уменьшения степеней, а X — квадратная матрица. Пример:
f=poly(d) f = 1.0000 -99.0000 626.0000 -626.0000 99.0000-1.0000 » polyvalm(f.D) ans = l.0e-006* -0.0003 -0.0011-0.0038-0.0059-0.0162 -0.0012 -0.0048-0.0163-0.0253-0.0692 -0.0034 -0.0131 -0.0447 -0.0696 -0.1897 -0.0076 -0.0288-0.0983-0.1529-0.4169 -0.0145-0.0551-0.1883-0.2929-0.7984 Данный пример иллюстрирует также погрешности численных методов, поскольку точное решение 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
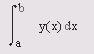
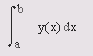
Широкое применение полиномов отчасти обусловлено большими возможностями полиномов в представлении данных, а также их простотой и единообразием вычислений. В этом разделе описаны основные функции для работы с полиномами. При этом полиномы обычно задаются векторами их коэффициентов.
