Функции обработки множеств

Множество — первичное понятие математики, не имеющее четкого определения. Под множеством подразумевается совокупность некоторых объектов, например книг в библиотеке, людей в зале или элементов вектора. В этом разделе приводятся некоторые функции для обработки множеств, представленных векторами. Они широко используются при анализе и обработке данных.

· intersect(a.b) — возвращает пересечение множеств для двух векторов а и b, т. е., общие элементы векторов а и b. Результирующий вектор отсортирован по возрастанию. Если входные массивы не являются векторами, то они рассматриваются как совокупность векторов-столбцов а=а(:) или b=b(:);

· intersect(a,b, 'rows') — возвращает строки, общие для а и b, когда а и b представляют собой матрицы с одинаковым числом столбцов;

· [c.ia.ib] = intersect(a.b) — также возвращает вектор-столбец индексов ia и ib. но так, что с = a(ia) и с = b(ib) (или с = a(ia.:) ис = b(ib.:)).

Пример:

» А = [1 7 2 6]; В = [7 2 3 4 6 1];

» [c,ia,ib] = intersect(А,В)

1 2 6 7

ia =

1 3 4 2

ib =

6 2 5 1

· ismember(a.S) — возвращает вектор той же длины, что и исходный а, содержащий логические единицы на месте тех элементов вектора а, которые принадлежат множеству S, и логические нули на месте тех элементов вектора а, которые не принадлежат множеству S;

· ismember (А. S.' rows') — возвращает вектор, содержащий логические единицы там, где строки матрицы А являются также строками матрицы S, и логические нули в остальных позициях. А и S должны быть матрицами с одним числом столбцов.

Пример:

» set = [0 1 3 5 7 9 11 15 17 19];

» а=[1 2345678];

» k = ismember(a.set)

k =

1 0 1 0 1 0 1 0

· setdiff(a.b) — возвращает разность множеств, т. е., те элементы вектора а, которые не содержатся в векторе b. Результирующий вектор сортируется по возрастанию;

· setdiff(a,b, 'rows') — возвращает те строки из матрицы а, которые не содержатся в матрице Ь. Матрицы а и b должны иметь одинаковое число столбцов;

· [c,i] = setdiff(...) — возвращает также вектор индексов 1, такой что с = а(i) или с = а (i,;).

Если входной массив а является матрицей, то он расценивается как вектор-столбец а(:).

Пример:

» а=[2 3 5 7 8 9 10 13 20];

» b=[1456894]

» с = setdiff(a.b)

с=

2 3 7 10 13 20

· setxor(a.b) — исключающее ИЛИ для векторов а и b. Результирующий вектор отсортирован;

· setxor(a,b, 'rows') — возвращает строки, которые не являются пересечениями матриц а и b. Матрицы а и b должны иметь одинаковое число столбцов;

· [c.ia.ib] = setxor(...) — возвращает также векторы индексов ia и ib так, что с является отсортированной комбинацией элементов с = а(iа)ис = b(ib) или для комбинаций строк с = а(iа,:)ис = b(ib.;).

Если массив а является матрицей, то он расценивается как вектор-столбец а(:).

Пример:

» а = [-1 0 1 Inf -Inf NaN];

» b = [-2 pi 0 Inf];

» с = setxor(a.b)

с =

-Inf -2.0000-1.00001.0000 3.1416 NaN

· union(a ,b) — возвращает вектор объединенных значений из а и b без повторяющихся элементов. Результирующий вектор сортируется в порядке возрастания;

· union(a,b, 'rows') — возвращает объединенные строки из а и b, не содержащие повторений (а и b — это матрицы с одинаковым числом столбцов);

· [c.ia.ib] = unionL.) — дополнительно возвращает i а и i b — векторы индексов, такие что с = a(ia) и c=b(1b), или, для объединенных строк, с = а(1а.:)ис = b(ib,:). Невекторный массив а расценивается как вектор-столбец а(:). Пример:

» а=[2,4,-4,9,0]:b=[2,5,4]:

» [c,ia,ib]=union(a,b)

с =

-4 0 2 4 5 9

ia =

3 5 4

ib =

1 3 2

· unique(a) — возвращает значения элементов из а, не содержащие повторений. Результирующий вектор сортируется в порядке возрастания. Невекторный массив расценивается как вектор-столбец а=а(: );

· unique(a, 'rows') — возвращает уникальные строки а;

· [b.i ,j] = unique(...) — дополнительно возвращает i и j — векторы индексов, такие что b = a(i)na = b(j) (или b = а(1,:) иа = b(j.:)).

Примеры:

» b=[-2,3,5,4,1,-6,2,2,7]

b=

-2 3 5 4 1 -6 2 2 7

» [c,i,j]=unique(b)

с =

Функции времени и даты

Ряд функций служит для возврата текущего времени и даты. Они перечислены ниже.

· calendar(d) — возвращает календарь на месяц, в который попадает день, заданный аргументом d (дни отсчитываются от начала летоисчисления);

· calendar — возвращает матрицу размером 6x7, содержащую календарь на текущий месяц. Календарь начинается с воскресения (первый столбец) и завершается субботой;

· calendar(y ,m) — возвращает календарь на месяц, заданный аргументом т, и год, заданный аргументом у;

Вызов функции без присваивания результата выдает календарь на экран. Примеры:

» calendar

Jul 2000

calendar(700477)

Nov 1917

· clock — возвращает вектор из 6 элементов, содержащий текущую дату и время в десятичной форме [год месяц день час минуты секунды]. Первые пять элементов этого вектора — целые числа. Шестой элемент имеет несколько десятичных знаков после запятой. Функция fix(clock) округляет число секунд до целого значения. Пример:

» c=clock

с =

1.0e+003 *

2.0000 0.0070 0.0240 0.0200 0.0120 0.0148

» fix(clock)

ans =

2000 7 24 20 12 26

· cputime — возвращает время работы процессора (в секундах) , использованное системой MATLAB с момента ее запуска. Это число может выйти за рамки внутреннего представления, и тогда отсчет времени начинается заново. Пример:

» +tl=cputime; w=surf(peaks(30));cputime-tl

ans =

0.2200

· str = date — возвращает строку, содержащую дату в формате дд-ммм-гггг (день-месяц-год). Пример:

» d = date

d =

24-Jul-2000

· datenum — преобразует строку даты в порядковый номер даты, который отсчитывается с некоторого начального дня (01.01.00);

· datenum(str) — преобразует дату, заданную строкой str, в порядковый номер даты. Строка string должна иметь один из следующих форматов: 0, 1, 2, 6, 13, 14, 15 или 16, определенных для функции datestr;

· datenum(Y.M.D) — возвращает порядковый номер даты для соответствующих массивов элементов Y, М и D (год, месяц, день). Массивы Y, М и D должны иметь одинаковую размерность (при этом любые из них могут быть скалярами);

· datenum(Y.M.D,H.MI,S) — возвращает порядковый номер даты для соответствующих массивов элементов Y, М, D, H, Ml и S (год, месяц, день, часы, минуты, секунды). Массивы Y, М, D, H, Ml и S должны иметь одинаковую размерность (при этом любые из них могут быть скалярами).

Пример:

» n1 = datenum('26-Nov-1998')

n1 =

» Y=[1998,2000];M-[1,12];D=23;N=datenum(Y,M,D)

N =

729778 730843

· datestr(D, dateform) — преобразует каждый элемент массива порядковых номеров даты D в строку. Аргумент dateform определяет формат результата; dateform может быть номером или строкой в соответствии с табл. 8.5.

Таблица 8.5.Форматы представления даты

· datevec(A) — преобразует входные величины в массив размерности пхб, каждая строка которого представляет собой вектор [Y,M.D,H,MI,S]. Первые пять элементов вектора — целые числа. Массив А может состоять или из строк, удовлетворяющих формату функции datestr, или из скалярных величин, созданных функциями datenum и now;

· [Y, M., D, H. MI, S] = datevec (A) — возвращает компоненты вектора даты как индивидуальные переменные.

Любой компонент входного вектора, который не вписывается в нормальный диапазон дат, преобразуется в следующий диапазон (так, например, несуществующая дата June 31 преобразуется в July 1). Допускаются значения нулевого месяца и нулевого дня. Например:

» n = datevecC 11/31/98')

n=

1998 12 1 0 0 0

» n = datevec(710223)

n =

1944 7 10 0 0

О eomday (Y, М) — возвращает последний день года и месяца, заданных соответственно элементами массивов Y и М. Пример (нахождение високосных лет двадцатого столетия):

» у = 1900:1999;

» Е = eomday(y.2);

» y(find(E==29))

ans=

Columns 1 through 6

1904 1908 1912 1916 1920 1924

Columns 7 through 12

1928 1932 1936 1940 1944 1948

Columns 13 through 18

1952 1956 1960 1964 1968 1972

Columns 19 through 24

1976 1980 1984 1988 1992 1996

· etime(t2,tl) — возвращает длительность промежутка времени (в секундах), задаваемого векторами t1 и t2. Векторы должны удовлетворять формату, выдаваемому функцией clock:

Т = [год месяц день час минуты секунды].

Функция работает некорректно, если в текущий промежуток времени попадут границы месяца или года, что, однако, случается крайне редко и исправляется при повторе операции. Пример (вычисляется время, затрачиваемое на быстрое преобразование Фурье с 2048 точками):

» х = rand(2048,l);t = clock; fft(x); etime(clock.t);etime (clock.t)

ans =

0.0500

· now — возвращает текущие время и дату в форме числа. Использование rem(now.l) возвращает только время, a floor(now) — только дату. Пример:

» t1 = now, t2 = rem(now,1)

t1 =

7.3009e+005

t2 =

0.6455

· tic — запускает таймер;

· toc — выводит время, прошедшее с момента запуска таймера;

· t = toe — возвращает прошедшее время в переменной t. Пример:

» tic.surf(peaks(50));toc

elapsed_time =

0.7600

· [N,S] = weekday(D) — возвращает день недели в виде числа N и в виде строки S для каждой даты массива D. Пример:

» D=[728647,735730]:[N.S] = weekday(D)

N =

2 1

S=

Mon Sun

Элементарные функции

Элементарные функции, пожалуй, наиболее известный класс математических функций. Поэтому, не останавливаясь подробно на их описании, представим набор данных функций, имеющийся в составе системы MATLAB. Функции, перечисленные ниже, сгруппированы по функциональному назначению. В тригонометрических функциях углы измеряются в радианах. Все функции могут использоваться в конструкции вида y=func(x), где func — имя функции. Обычно в такой форме задается информация о функции в системе MATLAB. Мы, однако, будем использовать для функций, возвращающих одиночный результат, более простую форму func(x). Форма [y,z,...]=func(x....) будет использоваться только в тех случаях, когда функция возвращает множественный результат.

Алгебраические и арифметические функции

В системе MATLAB определены следующие алгебраические и арифметические функции:

· abs(X) — возвращает абсолютную величину для каждого числового элемента вектора X. Если X содержит комплексные числа, abs(X) вычисляет модуль каждого числа. Примеры:

abs(-5) = 5

abs(3+4i) =5

» abs([1 -2 1 3i 2+3i ])

ans =

1.0000 2.0000 1.0000 3.0000 3.6056

· ехр(Х) — возвращает экспоненту для каждого элемента X. Для комплексного числа z = х + i*y функция exp(z) вычисляет комплексную экспоненту: exp(z)=exp(x)*(cos(y)+i*sin(y)).

Примеры:

» ехр([1 23])

ans =

2.7183 7.3891 20.0855

» exp(2+3i)

ans =

-7.3151 + 1.0427i

· factor(n) — возвращает вектор-строку, содержащую простые множители числа п. Для массивов эта функция неприменима. Пример:

f = factor(221)

f =

13 17

· G=gcd(A, В) — возвращает массив, содержащий наибольшие общие делители соответствующих элементов массивов целых чисел А и В. Функция gcd (0.0) возвращает значение 0, в остальных случаях возвращаемый массив G содержит положительные целые числа;

· [G, С. D] = gcd(A, В) — возвращает массив наибольших общих делителей G и массивов С и D, которые удовлетворяют уравнению A(i) .*С(1) + B(i) .*D(i) = G(i). Они полезны для выполнения элементарных эрмитовых преобразований. Примеры:

» А=[2 6 9]:

» В=[2 3 3]:

» gcd(A.B)

ans =

2 3 3

» [G.C.D]=gcd(A.B)

G =

2 3 3

C =

0 0 0

D=

1 1 1

· lcm(A.B) — возвращает наименьшие общие кратные для соответствующих парных элементов массивов А и В. Массивы А и В должны содержать положительные целые числа и иметь одинаковую размерность (любой из них может быть скаляром). Пример:

» А=[1 354];

» В=[2 462];

» lcm(А.В)

ans =

2 12 30 4

· log (X) — возвращает натуральный логарифм элементов массива X. Для комплексного или отрицательного z, где z = х + y*i, вычисляется комплексный логарифм в виде log(z) = log(abs(z)) + i*atan2(y,x). Функция логарифма вычисляется для каждого элемента массива. Область определения функции включает комплексные и отрицательные числа, что способно привести к непредвиденным результатам при некорректном использовании. Пример:

» Х=[1.2 3.34 5 2.3];

» log(X)

ans=

-0.1823 1.2060 1.6094 0.8329

· log2(X) — возвращает логарифм по основанию 2 элементов массива X;

· [F,E] = log2(X) — возвращает массив действительных значений F и массив целых чисел Е. Элементы массива F обычно лежат в диапазоне 0.5 J abs(F) < 1. Для действительных X возвращаемые массивы F удовлетворяют уравнению вида X = F. *2. Е. Для нулевых значений X возвращаются F = 0 и Е = 0.

Пример:

» Х=[2 4.678 5;0.987 1 3];

» [F.E] = log2(Х)

F =

0.5000 0.5847 0.6250

0.9870 0.5000 0.7500

Е =

2 3 3

0 1 2

· log10(X) — возвращает логарифм по основанию 10 для каждого элемента X. Область функции включает комплексные числа, что способно привести к непредвиденным результатам при некорректном использовании.

Пример:

» Х=[1.4 2.23 5.8 3];

» log10(X)

ans =

0.1461 0.3483 0.7634 0.4771

· mod(x.y) — возвращает х mod у;

· mod(X, Y) — возвращает остаток от деления X на Y (т. е., X - Y.*floor(X./Y)) для ненулевого Y, и X в противном случае. Если операнды X и Y имеют одинаковый знак, функция mod(X, Y) возвращает тот же результат, что mod(Х, Y). Однако (для положительных X и Y) mod(-x.y) = rem(-x,y)+y.

Примеры:

» М = mod(5.2)

М =

» mod(10.4)

ans =

· pow2(Y) — возвращает массив X, где каждый элемент есть Z ^Y ;

· pow2(F.E) — вычисляет Х=Р*2 ^£ для соответствующих элементов F и Е. Аргументы F и Е — массивы действительных и целых чисел соответственно.

Пример:

» d=pow2(pi/4,2)

d =

3.1416

· р = nextpow2(A) — возвращает такой показатель степени р, что 2 ^Р i abs(A). Эта функция эффективно применяется для выполнения быстрого преобразования

Фурье. Если А не является скалярной величиной, то nextpowZ возвращает значение nextpow2(length(A)).

Пример:

» х=[2 678934567784324];

» length(x)

ans =

» р = nextpow2(x)

Р =

» х=4:

» р = nextpow2(x)

Р =

» Х=45;

» р = nextpow2(x)

Р =

Функция primes(n) возвращает вектор-строку простых чисел, меньших или равных n. Пример:

» р = primes(25)

Р =

2 3 5 7 11 13 17 19 23

· [N,D] = rat(X) - возвращает массивы N и D, такие что N./D аппроксимирует X с точностью 1 .е-6*norm(Х(:),!). Даже при том, что все числа с плавающей запятой — рациональные числа, иногда желательно аппроксимировать их дробями, у которых числитель и знаменатель являются по возможности малыми целыми числами. Функция rat пытается это сделать;

· [N.D] = rat(X.tol) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью tol.

· rat (X) без выходных параметров просто выдает на экран массив цепных дробей;

· rats(X.strlen) — возвращает ряд, полученный путем упрощенной рациональной аппроксимации элементов X. Аргумент strlen — длина возвращаемой строки. Функция возвращает знак «*», если полученное значение не может быть напечатано в строке, длина которой задана значением strlen. По умолчанию strlen=13. Тот же алгоритм аппроксимации используется в командном окне MATLAB при задании рационального формата вывода командой format rat.

Пример:

» [g.j]=rat(pi.le-10)

g=

j =

· sqrt(A) — возвращает квадратный корень каждого элемента массива X. Для отрицательных и комплексных элементов X функция sqrt(X) вычисляет комплексный результат.

Пример:

» А=[25 21.23 55.8 3]:

» sqrt(A)

ans =

5.0 4.6076 7.4699 1.7321

На рис. 8.1 представлены графики ряда распространенных алгебраических функций. Эти графики получены в результате исполнения следующего файла-сценария:

syms x

subplot(2,2.1).ezplot(x*2.[-5 5]).xlabel( " ).grid on

subplot(2,2.2).ezplot(exp(x),[-2 2]),xlabel(").grid on

subplot(2.2.3).ezplot(log(x).[0 5]),grid on

subplot(2.2.4),ezplot(sqrt(x).[0 10]).grid on

Рис. 8.1.Графики ряда алгебраических функций

Графики дают наглядное представление о поведении представленных на них функций. Обратите внимание на применение графической команды ezplot из пакета Symbolic Math ToolBox (она отличается от обычной команды ezplot MATLAB отсутствием заключения символьных переменных в'), команды syms, также входящей в пакет Symbolic Math .Toolbox и задающей символьную переменную х, и несколько необычное применение команды xlabel (''). Эта команда с аргументом в виде пустой строки снимает вывод обозначения горизонтальной оси на двух верхних графиках. Если этого не сделать, то символ «х» окажется наложенным на наименование функций нижних графиков, которое команда ezpl ot выводит над графиками автоматически.

Тригонометрические и обратные им функции

В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.

Э acos (X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.

Примеры:

»Y = acos (0.5)

1.0472

» acos([0.5 1 2])

ans =

1.0472 0 0 + 1.31701

· acot (X) — возвращает арккотангенс для каждого элемента X. Пример:

» Y=acot(0.l)

у =

1.4711

· acsc(X) — возвращает арккосеканс для каждого элемента X. Пример:

» Y= acsc(3)

0.3398

· asec(X) — возвращает арксеканс для каждого элемента X. Пример:

» Y=asec(0.5)

Y =

0 + 1.31701

· asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:

» Y= asin (0.278)

Y =

0.2817

· atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:

» Y=atan(1)

Y =

0.7854

· atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].

Пример:

» atan2(l,2)

ans =

0.4636

· cos(X) — возвращает косинус для каждого элемента X. Пример:

»Х=[123];

» cos(X)

ans =

0.5403 -0.4161 -0.9900

· cot(X) — возвращает котангенс для каждого элемента X. Пример:

» Y = cot(2)

Y =

-0.4577

· csc(X) — возвращает косеканс для каждого элемента X. Пример:

» Х=[2 4.678 5:0.987 1 3];

» Y = csc(X)

Y =

1.0998 -1.0006 -1.0428

1.1985 1.1884 7.0862

· sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:

» X=[pi/10 pi/3 pi/5];

» sec(X)

ans =

1.0515 2.0000 1.2361

· sin(X) — возвращает синус для каждого элемента X. Пример:

» X=[pi/2 pi/4 pi/6 pi];

» sin(X)

ans =

1.0000 0.7071 0.5000 0.0000

· tan(X) — возвращает тангенс для каждого элемента X.

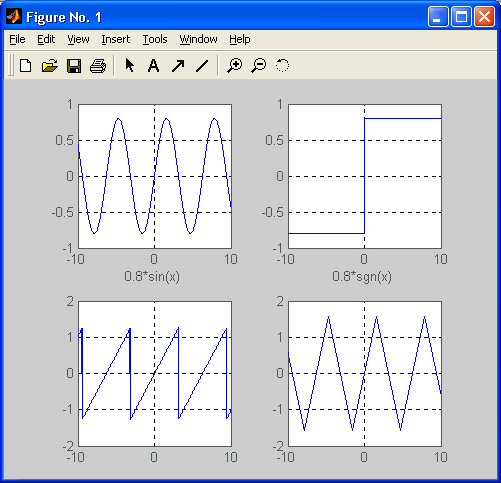
Рис. 8.2.Графики четырех тригонометрических функций

Пример:

» Х=[0.08 0.06 1.09]

X=

0.0800 0.0600 1.0900

» tan(X)

ans=

0.802 0.0601 1.9171

Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):

syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel("),gnd on

subplot(2.2.2),ezp"lot(tan(x).[-5 5]).xlabel(").grid on

subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on

subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on

Поскольку многие тригонометрические функции периодичны, появляется возможность формирования из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы, используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных сигнала — прямоугольные, пилообразные и треугольные импульсы:[ В пакете расширения Signal Processing Toolbox есть специальные функции для генерации таких сигналов — square и sawtooth. — Примеч. ред. ]

х=-10:0.01:10;

subplot(2,2.1).plot(x.0.8*sin(x))

.x label('0.8*sin(x)')

subplot(2.2,2).plot(x,0.8*sign(sin(x)))

.x1abel('0.8*sgn(sin(x))')

subplot(2.2.3),plot(x.atan(tan(x/2)))

.xlabel('atan(tan(x/2))')

subplot(2.2.4),plot(x,asin(sin(x)))

.xlabel('asin(sin(x))')

Соответствующие графики представлены на рис. 8.3.

Рис. 8.3.Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний

Дополнительный ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:

х=-10:0.01:10;

subplot(2.2.1).plot(x.sin(x). ^A 3).x1abel('sin(xr3')

subplot(2.2.2).plot(x,abs(s1n(x)))

.xlabel('abs(sin(x))').axis([-10 10 -1 1]),

subplot(2.2,3),plot(x,tan(cos(x)))

.xlabel('tanCcos(x))')

subplot(2.2.4).plot(x.csch(sec(x))),xlabeK'csch(sec(x))')

Рис. 8.4.Графики периодических сигналов без разрывов

Эти графики неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения (или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.

Не нашли, что искали? Воспользуйтесь поиском по сайту: