|
|
Сжатие способом кодирования серий (RLE)Суть методов данного подхода состоит в замене цепочек или серий повторяющихся байтов или их последовательностей на один кодирующий байт и счетчик числа их повторений. Например: Первый байт указывает сколько раз нужно повторить следующий байт. Если первый байт равен 00, то затем идет счетчик, показывающий, сколько за ним следует неповторяющихся данных. Данные методы, как правило, достаточно эффективны для сжатия растровых графических изображений (BMP, PCX, TIF, GIF), т.к. последние содержат достаточно много длинных серий повторяющихся последовательностей байтов. Недостатком метода RLE является достаточно низкая степень сжатия.
Алгоритм Хаффмана Сжимая файл по алгоритму Хаффмана, первое, что мы должны сделать, - это необходимо прочитать файл полностью и подсчитать, сколько раз встречается каждый символ из расширенного набора ASCII. Если мы будем учитывать все 256 символов, то для нас не будет разницы в сжатии текстового и EXE файла. После подсчета частоты вхождения каждого символа, необходимо просмотреть таблицу кодов ASCII и сформировать бинарное дерево. Пример: Мы имеем файл длиной в 100 байт и имеющий 6 различных символов в себе. Мы подсчитали вхождение каждого из символов в файл и получили следующее :
Теперь мы берем эти числа и будем называть их частотой вхождения для каждого символа.
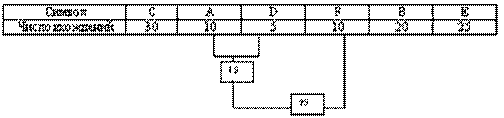
Мы возьмем из последней таблицы 2 символа с наименьшей частотой. В нашем случае это D (5), и какой-либо символ из F или A (10), можно взять любой из них, например A. Сформируем из "узлов" D и A новый "узел", частота вхождения для которого будет равна сумме частот D и A :
Номер в рамке - сумма частот символов D и A. Теперь мы снова ищем два символа с самыми низкими частотами вхождения. Исключем из просмотра D и A и рассматриваем вместо них новый "узел" с суммарной частотой вхождения. Самая низкая частота теперь у F и нового "узла". Снова сделаем операцию слияния узлов :
Рассматриваем таблицу снова для следующих двух символов (B и E). Мы продолжаем в эту процедуру пока все "дерево" не сформировано, т.е. пока все не сведется к одному узлу.
Теперь, когда наше дерево создано, мы можем кодировать файл. Мы должны всегда начинать из корня (Root). Кодируя первый символ (лист дерева С), мы прослеживаем вверх по дереву все повороты ветвей, и, если мы делаем левый поворот, то запоминаем 0-й бит, и аналогично 1-й бит для правого поворота. Так, для C мы будем идти влево к 55 (и запомним 0), затем снова влево (0) к самому символу. Код Хаффмана для нашего символа C - 00. Для следующего символа ( А ) у нас получается - влево, вправо, влево, влево, что выливается в последовательность 0100. Выполнив выше сказанное для всех символов, получим: C = 00 (2 бита) При кодировании заменяем символы данными последовательностями. Достоинствами метода Хаффмана являются его достаточно высокая скорость и хорошее качество сжатия. Этот алгоритм сравнительно давно известен и широко применяется; примерами могут служить программа compress ОС UNIX (программная реализация) и стандарт кодирования для факсов [Hunter] (аппаратная реализация). Кодирование Хаффмана имеет минимальную избыточность при условии, что каждый символ кодируется отдельной цепочкой в алфавите {0,1}). Недостатком кодирования Хаффмена является зависимость степени сжатия от близости вероятностей символов к отрицательным степеням 2; это связано с тем, что каждый символ кодируется *целым* числом бит. Наиболее ярко это проявляется при кодировании двухсимвольного алфавита: в этом случае сжатие *всегда* отсутствует, несмотря на различие вероятностей символов; алгоритм фактически "округляет" их до 1/2!Эта проблема может быть частично решена за счет блокирования входного потока (т.е. введения в рассмотрение новых символов вида 'ab', 'abc', ... где a, b, c -- символы исходного алфавита). Однако это не позволяет полностью избавиться от потерь (они лишь уменьшаются пропорционально размеру блока) и приводит к резкому росту кодового дерева: если, например, символами входного алфавита являются 8-битовые байты со значениями 0 .. 255, то при блокировании по два символа мы получаем 65536 символов (и столько же листьев кодового дерева), а при блокировании по три -- 16777216! Соответственно возрастут требования к памяти и время построения дерева (а при адаптивном кодировании – и время обновления дерева, а значит, и время сжатия). Потери же составят в среднем 1/2 бита на символ при отсутствии блокирования, а при его наличии -- 1/4 и 1/6 бита соответственно для блоков длин 2 и 3.Большую степень сжатия, не зависящую от близости значений вероятности символов к степеням 1/2, может дать так называемое арифметическое кодирование.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|