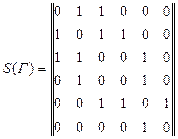|
|
Управление динамически выделяемой памятьюДинамические структуры по определению характеризуются непостоянством и непредсказуемостью размера. Поэтому память под отдельные элементы таких структур выделяется в момент, когда они "начинают существовать" в процессе выполнения программы, а не во время трансляции. Когда в элементе структуры больше нет необходимости, занимаемая им память освобождается. В современных вычислительных средах большая часть вопросов, связанных с управлением памятью, решается операционными системами или системами программирования. Для программиста прикладных задач динамическое управление памятью либо вообще прозрачно, либо осуществляется через достаточно простой и удобный интерфейс стандартных процедур/функций. Однако, перед системным программистом вопросы управления памятью встают гораздо чаще. Во-первых, эти вопросы в полном объеме должны быть решены при проектировании операционных систем и систем программирования, во-вторых, некоторые сложные приложения могут сами распределять память в пределах выделенного им ресурса, наконец в-третьих, знание того, как в данной вычислительной среде распределяется память, позволит программисту построить более эффективное программное изделие даже при использовании интерфейса стандартных процедур. В общем случае при распределении памяти должны быть решены следующие вопросы: · способ учета свободной памяти; · дисциплины выделения памяти по запросу; · обеспечение утилизации освобожденной памяти. В распоряжении программы обычно имеется адресное пространство, которое может рассматриваться как последовательность ячеек памяти с адресами, линейно возрастающими от 0 до N. Какие-то части этого адресного пространства обычно заняты системными программами и данными, какие-то - кодами и статическими данными самой программы, оставшаяся часть доступна для динамического распределения. Обычно доступная для распределения память представляет собой непрерывный участок пространства с адресными границами от n1 до n2. В управлении памятью при каждом запросе на память необходимо решать, по каким адресам внутри доступного участка будет располагаться выделяемая память. В некоторых системах программирования выделение памяти автоматизировано полностью: система не только сама определяет адрес выделяемой области памяти, но и определяет момент, когда память должна выделяться. Так, например, выделяется память под элементы списков в языке LISP, под символьные строки в языках SNOBOL и REXX. В других системах программирования - к ним относится большинство универсальных процедурных языков программирования - моменты выделения и освобождения памяти определяются программистом. Программист должен выдать запрос на выделение/освобождение памяти при помощи стандартной процедуры/функции - ALLOCATE/FREE в PL/1, malloc/free в C, New/Dispose в PASCAL и т.п. Система сама определяет размещение выделяемого блока, и функция выделения памяти возвращает его адрес. Наконец, в уже названных выше задачах системного программирования программист зачастую должен определить также и адрес выделяемой области. Память всегда выделяется блоками, т.е. обязательно непрерывными последовательностями смежных ячеек. Блоки могут быть фиксированной или переменной длины. Фиксированный размер блока гораздо удобнее для управления: в этом случае вся доступная для распределения память разбивается на "кадры", размер каждого из которых равен размеру блока, и любой свободный кадр годится для удовлетворения любого запроса. К сожалению, лишь ограниченный круг реальных задач может быть сведен к блокам фиксированной длины. Одной из проблем, которые должны приниматься во внимание при управлении памятью, является проблема фрагментации (дробления) памяти. Она заключается в возникновении "дыр" - участков памяти, которые не могут быть использованы. Различаются дыры внутренние и внешние. Внутренняя дыра - неиспользуемая часть выделенного блока, она возникает, если размер выделенного блока больше запрошенного. Внутренние дыры характерны для выделения памяти блоками фиксированной длины. Внешняя дыра - свободный блок, который в принципе мог бы быть выделен, но размер его слишком мал для удовлетворения запроса. Внешние дыры характерны для выделения блоками переменной длины. Управление памятью должно быть построено таким образом, чтобы минимизировать суммарный объем дыр. Система управления памятью должна прежде всего "знать", какие ячейки имеющейся в ее распоряжении памяти свободны, а какие - заняты. Методы учета свободной памяти основываются либо на принципе битовой карты, либо на принципе списков свободных блоков. В методах битовой карты создается "карта" памяти - массив бит, в котором каждый однобитовый элемент соответствует единице доступной памяти и отражает ее состояние: 0 - свободна, 1 - занята. Если считать единицей распределения единицу адресации - байт, то сама карта памяти будет занимать 1/8 часть всей памяти, что делает ее слишком дорогостоящей. Поэтому при применении методов битовой карты обычно единицу распределения делают более крупной, например, 16 байт. Карта, таким образом, отражает состояние каждого 16-байтного кадра. Карта может рассматриваться как строка бит, тогда поиск участка памяти для выделения выполняется как поиск в этой строке подстроки нулей требуемой длины. В другой группе методов участки свободной памяти объединяются в связные списки. В системе имеется переменная, в которой хранится адрес первого свободного участка. В начале первого свободного участка записывается его размер и адрес следующего свободного участка. В простейшем случае список свободных блоков никак не упорядочивается. Поиск выполняется перебором списка. Дисциплины выделения памяти решают вопрос: какой из свободных участков должен быть выделен по запросу. Выбор дисциплины распределения не зависит от способа учета свободной памяти. Две основные дисциплины сводятся к принципам "самый подходящий" и "первый подходящий". По дисциплине "самый подходящий" выделяется тот свободный участок, размер которого равен запрошенному или превышает его на минимальную величину. По дисциплине "первый подходящий" выделяется первый же найденный свободный участок, размер которого не меньше запрошенного. При применении любой дисциплины, если размер выбранного для выделения участка превышает запрос, выделяется запрошенный объем памяти, а остаток образует свободный блок меньшего размера. В некоторых системах вводится ограничение на минимальный размер свободного блока: если размер остатка меньше некоторого граничного значения, то весь свободный блок выделяется по запросу без остатка. Практически во всех случаях дисциплина "первый подходящий" эффективнее дисциплины "самый подходящий". Это объясняется, во-первых, тем, что при поиске первого подходящего не требуется просмотр всего списка или карты до конца, во-вторых, тем, что при выборе всякий раз "самого подходящего" остается больше свободных блоков маленького размера - внешних дыр. Когда в динамической структуре данных или в отдельном ее элементе нет больше необходимости, занимаемая ею память должна быть утилизована, т.е. освобождена и сделана доступной для нового распределения. В тех системах, где память запрашивается программистом явным образом, она и освобождена должна быть явным образом. Даже в некоторых системах, где память выделяется автоматически, она освобождается явным образом (например, операция DROP в языке REXX). В таких системах, конечно, задача утилизации решается просто. При представлении памяти на битовой карте достаточно просто сбросить в 0 биты, соответствующие освобожденным кадрам. При учете свободной памяти списками блоков освобожденный участок должен быть включен в список, но одного этого недостаточно. Следует еще позаботиться о том, чтобы при образовании в памяти двух смежных свободных блоков они слились в один свободный блок суммарного размера. Задача слияния смежных блоков значительно упрощается при упорядочении списка свободных блоков по адресам памяти - тогда смежные блоки обязательно будут соседними элементами этого списка. Задача утилизации значительно усложняется в системах, где нет явного освобождения памяти: тогда на систему ложится задача определения того, какие динамические структуры или их элементы уже не нужны программисту. Один из методов решения этой задачи предполагает, что система не приступает к освобождению памяти до тех пор, пока свободной памяти совсем не останется. Затем все зарезервированные блоки проверяются и освобождаются те из них, которые больше не используются. Такой метод называется "сборкой мусора". Программа сборки мусора вызывается тогда, когда нет возможности удовлетворить некоторый частный запрос на память, или когда размер доступной области памяти стал меньше некоторой заранее определенной границы. Алгоритм сборки мусора обычно бывает двухэтапным. На первом этапе осуществляется маркировка (пометка) всех блоков, на которые указывает хотя бы один указатель. На втором этапе все неотмеченные блоки возвращаются в свободный список, а метки стираются. Важно, чтобы в момент включения сборщика мусора все указатели были установлены на те блоки, на которые они должны указывать. Если необходимо в некоторых алгоритмах применять методы с временным рассогласованием указателей, необходимо временно отключить сборщик мусора - пока имеется такое рассогласование. Один из самых серьезных недостатков метода сборки мусора состоит в том, что расходы на него увеличиваются по мере уменьшения размеров свободной области памяти. Другой метод - освобождать любой блок, как только он перестает использоваться. Он обычно реализуется посредством счетчиков ссылок - счетчиков, в которых записывается, сколько указателей на данный блок имеется в данный момент времени. Когда значение счетчика становится равным 0, соответствующий блок оказывается недоступным и, следовательно, не используемым. Блок возвращается в свободный список. Такой метод предотвращает накопление мусора, не требует большого числа оперативных проверок во время обработки данных. Однако и у этого метода есть определенные недостатки. Во-первых, если зарезервированные блоки образуют циклическую структуру, то счетчик ссылок каждого из них не равен 0, когда все связи, идущие извне блоков в циклическую структуру, будут уничтожены. Это приводит к появлению мусора. Существуют различные возможности устранить этот недостаток: запретить циклические и рекурсивные структуры; отмечать циклические структуры флажками, и обрабатывать их особым образом; потребовать, чтобы любая циклическая структура всегда имела головной блок, счетчик циклов которого учитывал бы только ссылки от элементов, расположенных вне цикла, и чтобы доступ ко всем блокам этой структуры осуществлялся только через него. Во-вторых, требуются лишние затраты времени и памяти на ведение счетчиков ссылок. В некоторых случаях может быть полезен метод восстановления ранее зарезервированной памяти, называемый уплотнением. Уплотнение осуществляется путем физического передвижения блоков данных с целью сбора всех свободных блоков в один большой блок. Преимущество этого метода в том, что после его применения выделение памяти по запросам упрощается. Единственная серьезная проблема, возникающая при использовании метода, - переопределение указателей. Механизм уплотнения использует несколько просмотров памяти. Сначала определяются новые адреса всех используемых блоков, которые были отмечены в предыдущем проходе, а затем во время следующего просмотра памяти все указатели, связанные с отмеченными блоками, переопределяются. После этого отмеченные блоки переставляются. Механизма освобождения памяти в методе восстановления совсем нет. Вместо него используется механизм маркировки, который отмечает блоки, используемые в данный момент. Затем, вместо того, чтобы освобождать каждый неотмеченный блок путем введения в действие механизма освобождения памяти, помещающего этот блок в свободный список, используется уплотнитель, который собирает неотмеченные блоки в один большой блок в одном конце области памяти. Недостаток метода в том, что из-за трех просмотров памяти велики затраты времени. Однако повышенная скорость резервирования в определенных условиях может компенсировать этот недостаток. Практическая эффективность методов зависит от многих параметров, таких как частота запросов, статистическое распределение размеров запрашиваемых блоков, способ использования системы - групповая обработка или стратегия обслуживания при управлении вычислительным центром.
Деревья
Теперь обратимся к изучению деревьев, наиболее важных нелинейных структур, встречающихся в вычислительных алгоритмах. Грубо говоря, структура дерева означает "разветвление", такое отношение между "узлами", как и в обычных деревьях. Дерево - одна из самых распространенных структур, используемых для представления данных в ЭВМ. А вообще, дерево - конечное множество, состоящее из одного или более элементов, называемых узлами. Между узлами существует отношение типа "исходный-порождённый". Корень - узел, не имеющий исходного (отца). Все узлы, кроме корня, имеют только один исходный (исх.отца). Есть деревья, состоящие из одного корня. Каждый узел может иметь несколько порождённых (сыновей). Отношение "исходный-порождённый" действует только так: не бывает отношения "порождённый-исходный", т.к потомок узла никогда не станет его предком. Сетевые структуры широко применяются при организации банков данных, систем управления базами данных, в системах программного имитационного моделирования сложных комплексов и т.д. Особое значение сетевые структуры приобрели в системах искусственного интеллекта, в которых они адекватно отражают логику организации данных и сложные отношения, возникающие в таких системах между различными элементами данных. В этих системах сетевые структуры применяются для построения семантических сетей, фреймов и других логических конструкций, необходимых для представления знаний, образования понятий и осуществления логических выводов. Сетевые структуры – весьма общий и гибкий класс связных списков. Рассмотрим частные случаи многосвязных списков – древовидные структуры, или просто деревья. Различное представление деревьев показано на рис. 6.1.
Корни у деревьев могут располагаться в разных местах. Могут вверх (рис.6.1,а), могут вниз (рис. 6.1,в), могут слева или справа (рис. 6.1,с).
Определим формально дерево как конечное множество Т, состоящее из одного или более узлов, таких, что а). имеется один специально обозначенный узел, называемый корнем данного дерева, б).остальные узлы (исключая корень) содержатся в m³0 попарно непересекающихся множествах Т1, …, Тm, каждое из которых в свою очередь является деревом. Деревья Т1, …, Тm называются поддеревьями данного корня. Из определения следует, что каждый узел дерева является корнем некоторого поддерева, которое содержится в этом дереве. Число поддеревьев данного узла называется степенью этого узла. Узел с нулевой степенью называется концевым узлом; иногда его называют листом. Неконцевые узлы часто называют узлами разветвления. Уровень узла по отношению к дереву Т определяется следующим образом: говорят, что корень имеет уровень 1, а другие узлы имеют уровень на 1 выше их уровня относительно содержащего их поддерева Тj этого корня. Если в пункте б) определения имеет значение относительный порядок поддеревьев Т1, …, Тm, то говорят, что дерево является упорядоченным. Если два дерева, отличающиеся друг от друга только относительным порядком поддеревьев узлов, не считать различными, то в этом случае говорят, что дерево является ориентированным, поскольку здесь имеет значение только относительная ориентация узла, а не их порядок. Лес – это множество (обычно упорядоченное), состоящее из некоторого (быть может равного нулю) числа непересекающихся деревьев. Пункт б) определения дерева можно сформулировать иначе, сказав, что узлы дерева, за исключением корня, образуют лес.
Деревья, как правило, дают хорошее представление о структуре отношения между элементами данных.
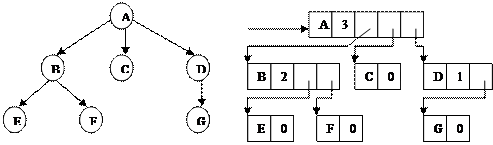
Рис. 6.2. Представление графа в форме многосвязного списка
Обычно дерево представляется в машинной памяти в форме многосвязного списка, в котором каждый указатель соответствует дуге. Это представление называется естественным представлением дерева. Существуют несколько разновидностей такого представления. В одной из наиболее общих разновидностей каждому узлу дерева ставится в соответствие элемент многосвязного списка, причем в каждом элементе отводятся следующие поля: поле данных, поле степени исхода (т.е. числа сыновей) и поля указателей, число которых равно степени исхода. На рисунке дан пример дерева и представление этого дерева в виде многосвязного списка, начало которого, соответствующее корню дерева, адресуется указателем Р. Предполагается, что этот указатель входит в дескриптор, содержащий и другую общую информацию о списке (например, число элементов). Обозначения А, В, С, D, E, F, записанные в первом поле каждого элемента списка, представляют собой данные о соответствующих узлах дерева. В некоторых случаях используется и последовательное представление деревьев в памяти. Такой способ может быть рекомендован, например, в случае постоянства или редкой изменчивости структуры дерева.
Бинарные деревья Выделим бинарное дерево - конечное множество узлов, которое является пустым или состоит из корня и двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями данного корня. Примерами бинарных деревьев являются, например, генеалогическое дерево с отцом и матерью человека в качестве его потомков, история турнира по хоккею, где узлом является каждая игра, определяемая ее победителем, а поддеревья – это 2 предыдущие игры соперников и т.д.
Определим бинарное дерево как конечное множество узлов, которое или пусто, или состоит из корня и из двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями данного корня. Помимо таких структур, как деревья, леса и бинарные деревья, имеется тип, тесно связанный с первыми двумя. Эти структуры называют обычно списочными структурами. Такой список определяется как конечная последовательность списков, число которых, может быть равно нулю. Представление бинарного дерева в компьютере вытекает из его определения. То есть мы имеем переменную Т, которая указывает на корень бинарного дерева. А каждый узел имеет две переменные связи: LLink и RLink, которые указывают на левое и правое поддеревья соответственно. Если дерево пусто, то указатель на него равен nil. В алгоритмах работы с древовидными структурами наиболее часто встречается понятие обход дерева. При таком методе исследования дерева каждый узел посещается ровно один раз, а полный обход задает линейное упорядочение узлов, что позволяет упростить алгоритм, так как при этом можно использовать понятие следующий узел, т.е. узел, который располагается перед данным узлом в таком упорядочении или после него. Для обхода бинарных деревьев можно применить один из трех принципиально разных способов: в прямом порядке, в центрированном порядке или в обратном порядке. Эти три метода определяются рекурсивно. Если дерево пусто, то для его обхода ничего делать не нужно, в противном случае обход выполняется в три этапа. Прямой порядок обхода: Попасть в корень Пройти левое поддерево Пройти правое поддерево Центрированный порядок обхода: Пройти левое поддерево Попасть в корень Пройти правое поддерево Обратный порядок обхода: Пройти левое поддерево Пройти правое поддерево Попасть в корень Эти методы обхода реализуются в компьютере либо с помощью рекурсии, либо с помощью стека, где сохраняются указатели на родителей.
Прошитые” деревья Можно несколько сэкономить память компьютера за счет применения так называемых “прошитых” деревьев. В “прошитых” деревьях концевые связи-указатели используются для связи с родителями, такие связи назвали нитями. А для того чтобы отличать нормальные связи от нитей, в каждом узле хранят две однобитовые переменные LTag и RTag. Эти переменные равны нулю, если соответствующие связи указывают на поддеревья, и единице, если связи являются нитями. Левая нить каждого узла указывает на узел, являющийся предшественником данного при центрированном обходе, правая - на узел, являющийся последователем данного узла. При работе с древовидными структурами часто приходится решать задачу обхода дерева. Это - способ методичного исследования узлов дерева, при котором каждый узел проходится точно один раз. Для этого удобно использовать, например, такой рекурсивный алгоритм: 1. Корень дерева. 2. Если нет поддеревьев, то ВЫХОД, иначе обходим все поддеревья слева направо.
Графы Графы - обобобщение структуры деревьев. Граф обычно определяется как некоторое множество точек (называемых вершинами) и некоторое множество линий (называемых ребрами), соединяющих определенные пары вершин. Каждая пара вершин соединяется не больше чем одним ребром. Можно рассматривать взвешенные и невзвешенные, ориентированные и неориентированные графы. Граф, в котором нет кратных ребер, можно задать при помощи весовой матрицы. Для каждой пары вершин в матрице указывается вес ребра, соединяющего вершины (если ребра нет, то полагаем соответствующий элемент матрицы равным бесконечности). Матрица может быть несимметричной в случае ориентированного графа. В случае невзвешенного графа удобнее представлять его при помощи матрицы связности, элемент которой равен 1, если есть соответствующие ребро, и 0, если ребро отсутствует. Пример использования графа – это задание условий в задаче коммивояжера, причем населенные пункты помещаются в вершины графа, а веса ребер определяют расстояние между соответствующими населенными пунктами. Теория графов достаточно обширна и многие алгоритмы, рассматриваемые в ней, имеют интерес сами по себе. Для решения прикладных задач часто возникает необходимость определить связаны ли две вершины графа, а в случае наличия весов, определить еще и вес пути между ними.
Граф (свободное дерево) обычно определяется как некоторое множество точек (называемых вершинами или узлами) и некоторое множество линий, называемых ребрами (или дугами), соединяющих определенные пары вершин. Каждая пара вершин соединяется не больше чем одним ребром. Дуга, соединенная с вершиной, называется инцидентной этой вершине. Две вершины называются смежными, если существует ребро, соединяющее их. Две дуги называются смежными, если они инцидентны одной и той же вершине. Пусть V и V` - вершины и пусть n³0; говорят, что «V0, V1, …, Vn» - путь длины n от V до V`, если V=V0, вершина Vk смежна с Vk+1 при 0£k<n, а Vn=V`. Путь прост, если вершины V0, V1, …, Vn-1 все различны между собой, а также различны все вершины V1, V2, …, Vn. Граф называется связным, если имеется путь между каждыми двумя вершинами этого графа. Циклом называется простой путь длины не менее 3 от какой-либо вершины до нее самой. Свободное дерево – это связный граф, не имеющий циклов. Формально направленный граф определяется как некое множество вершин и множество дуг, причем каждая дуга ведет от некоторой вершины V к некоторой вершине V`. Если e – дуга, идущая от V к V`, то говорят, что V – начальная вершина дуги e, а V` - конечная вершина.
Рис. 6.4. Направленный и ненаправленный графы
Для задания графов существует несколько классов матриц, основные из которых класс матриц инциденции и класс матриц смежности. Класс матриц инциденции. Если граф Г содержит n вершин и m дуг, то матрица инциденции А(Г)=[aij]mxn определяется так:
aij = -1, если вершина vj – конец дуги ui; 0, если дуга ui не инцидентна вершине vj.
Направленный граф на рис. 6.4 можно задать матрицей инциденции:
Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется следующим образом:
0, если вершины несмежны. Во взвешенном графе каждая единица заменяется на вес соответствующего ребра. Ненаправленный граф на рис. 6.4 описывается следующей матрицей смежности:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

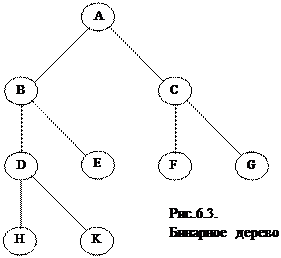

 1, если вершина vj – начало дуги ui;
1, если вершина vj – начало дуги ui;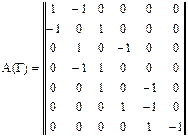
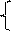 Sij = 1, если vi смежна vj;
Sij = 1, если vi смежна vj;