Классификация грамматик и языков по Хомскому

(грамматики классифицируются по виду их правил вывода)

ТИП 0:

Грамматика G = (VT, VN, P, S) называется грамматикой типа 0, если на правила вывода не накладывается никаких ограничений (кроме тех, которые указаны в определении грамматики).

ТИП 1:

Грамматика G = (VT, VN, P, S) называется неукорачивающей грамматикой, если каждое правило из P имеет вид a ® b, где a Î (VT È VN)⁺, b Î (VT È VN)⁺ и | a | £ | b |.

Грамматика G = (VT, VN, P, S) называется контекстно-зависимой (КЗ), если каждое правило из P имеет вид a ® b, где a = x₁Ax₂; b = x₁gx₂; A Î VN; g Î (VT È VN)⁺; x₁,x₂ Î (VT È VN)^*.

Грамматику типа 1 можно определить как неукорачивающую либо как контекстно-зависимую.

Выбор определения не влияет на множество языков, порождаемых грамматиками этого класса, поскольку доказано, что множество языков, порождаемых неукорачивающими грамматиками, совпадает с множеством языков, порождаемых КЗ-грамматиками.

ТИП 2:

Грамматика G = (VT, VN, P, S) называется контекстно-свободной (КС), если каждое правило из Р имеет вид A ® b, где A Î VN, b Î (VT È VN)⁺.

Грамматика G = (VT, VN, P, S) называется укорачивающей контекстно-свободной (УКС), если каждое правило из Р имеет вид A ® b, где A Î VN, b Î (VT È VN)^*.

Грамматику типа 2 можно определить как контекстно-свободную либо как укорачивающую контекстно-свободную.

Возможность выбора обусловлена тем, что для каждой УКС-грамматики существует почти эквивалентная КС-грамматика.

ТИП 3:

Грамматика G = (VT, VN, P, S) называется праволинейной, если каждое правило из Р имеет вид A ® tB либо A ® t, где A Î VN, B Î VN, t Î VT.

Грамматика G = (VT, VN, P, S) называется леволинейной, если каждое правило из Р имеет вид A ® Bt либо A ® t, где A Î VN, B Î VN, t Î VT.

Грамматику типа 3 (регулярную, Р-грамматику) можно определить как праволинейную либо как леволинейную.

Выбор определения не влияет на множество языков, порождаемых грамматиками этого класса, поскольку доказано, что множество языков, порождаемых праволинейными грамматиками, совпадает с множеством языков, порождаемых леволинейными грамматиками.

Соотношения между типами грамматик:

любая регулярная грамматика является КС-грамматикой;

любая регулярная грамматика является УКС-грамматикой;

любая КС-грамматика является КЗ-грамматикой;

любая КС-грамматика является неукорачивающей грамматикой;

любая КЗ-грамматика является грамматикой типа 0.

любая неукорачивающая грамматика является грамматикой типа 0.

Замечание: УКС-грамматика, содержащая правила вида A ® l, не является КЗ-грамматикой и не является неукорачивающей грамматикой.

Определение: язык L(G) является языком типа k, если его можно описать грамматикой типа k.

Замечание: следует подчеркнуть, что если язык задан грамматикой типа k, то это не значит, что не существует грамматики типа k’ (k’>k), описывающей тот же язык. Поэтому, когда говорят о языке типа k, обычно имеют в виду максимально возможный номер k.

Вопрос 6 *КАША* думайте сами что и куда писать

Постановка задачи разбора

Грамматики и распознаватели – два независимых метода, которые реально

могут быть использованы для определения какого-либо языка. Однако при разработке компилятора для некоторого языка программирования возникает задача, которая требует связать между собой эти методы задания языков.

Распознаватель – это специальный алгоритм, который позволяет определить принадлежность цепочки символов некоторому языку. Распознаватели представляют собой один из способов определения языка.

В общем виде распознаватель можно отобразить в виде условной схемы,

состоящей из следующих основных компонентов:

1. Элемента, содержащего исходную цепочку входных символов, и считывающего устройства, обозревающего очередной символ в этой цепочке;

2. Устройства управления, которое координирует работу распознавателя,

имеет некоторый набор состояний и конечную память (для хранения своего состояния и некоторой промежуточной информации);

3. Внешней (рабочей) памяти, которая может хранить некоторую информацию в процессе работы распознавателя и в отличие от памяти устройства

управления может иметь неограниченный объем.

Распознаватель работает с символами своего алфавита – алфавита распознавателя. Алфавит распознавателя конечен и включает в себя все допустимые символы входных цепочек, а также некоторый дополнительный алфавит символов, которые могут обрабатываться устройством управления и храниться в рабочей памяти распознавателя.

По видам считывающего устройства распознаватели могут быть двусторонние и односторонние.

Односторонние распознаватели допускают чтение входных символов только в одном направлении.

Двусторонние распознаватели допускают, что считывающее устройство может перемещаться относительно цепочки входных символов в обоих направлениях: как вперед, от начала ленты к концу, так и назад, возвращаясь к уже прочитанным символам.

По видам устройства управления распознаватели бывают детерминированные и недетерминированные.

Распознаватель называется детерминированным в том случае, если для каждой допустимой конфигурации распознавателя, которая возникла на некотором шаге его работы, существует единственно возможная конфигурация, в которую распознаватель перейдет на следующем шаге работы.

В противном случае распознаватель называется недетерминированным.

Недетерминированный распознаватель может иметь такую допустимую конфигурацию, для которой существует некоторое конечное множество конфигураций, возможных на следующем шаге работы. Достаточно иметь хотя бы одну такую конфигурацию, чтобы распознаватель был недетерминированным.

По видам внешней памяти распознаватели бывают следующих типов:

1. распознаватели без внешней памяти;

2. распознаватели с ограниченной внешней памятью;

3. распознаватели с неограниченной внешней памятью.

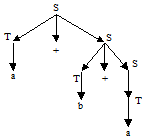
Разработчики трансляторов всегда имеют дело с уже определенным языком программирования. Грамматика для синтаксических конструкций этого языка известна. Она, как правило, четко описана в стандарте языка, и хотя форма описания может быть произвольной, ее всегда можно преобразовать к требуемому виду (например, к форме Бэкуса-Наура). Задача разработчиков заключается в том, чтобы построить распознаватель для заданного языка, который затем будет основой синтаксического анализатора в трансляторе.

Таким образом, задача разбора в общем виде заключается в следующем: на основе имеющейся грамматики некоторого языка построить распознаватель для этого языка.

Задача разбора в общем виде может быть решена не для всех типов языков.

Но как было сказано выше, разработчиков трансляторов интересуют, прежде

всего, контекстно-свободные и регулярные языки. Для данных типов языков

доказано, что задача разбора для них разрешима. Поскольку языки программирования не являются чисто формальными языками и несут в себе некоторый смысл (семантику), то задача разбора для создания реальных компиляторов понимается несколько шире, чем она формулируется для чисто формальных языков. Компилятор должен не просто дать ответ, принадлежит или нет входная цепочка символов заданному языку, но и определить ее смысловую нагрузку. Для этого необходимо выявить те правила грамматики, на основании которых цепочка была построена. Фактически работа распознавателей в составе компиляторов сводится к построению в том или ином виде дерева разбора входной цепочки.

Кроме того, если входная цепочка символов не принадлежит заданному

языку – исходная программа содержит ошибку, – разработчику программы не

интересно просто узнать сам факт наличия ошибки. В данном случае задача

разбора также расширяется: распознаватель в составе компилятора должен не

только установить факт присутствия ошибки во входной программе, но и по

возможности определить тип ошибки и то место в цепочке символов, где она

встречается.

Вопрос 6. Парт 2

Разбор цепочек

Цепочка принадлежит языку, порождаемому грамматикой, только в том случае, если существует ее вывод из цели этой грамматики.

Процесс построения такого вывода (а, следовательно, и определения принадлежности цепочки языку) называется разбором.

С практической точки зрения наибольший интерес представляет разбор поконтекстно-свободным (КС и УКС) грамматикам. Их порождающей мощности достаточно для описания большей части синтаксической структуры языков программирования. Для различных подклассов КС-грамматик имеются хорошо разработанные практически приемлемые способы решения задачи разбора.

Рассмотрим основные понятия и определения, связанные с разбором по КС-грамматике.

Определение: вывод цепочки b Î (VT)^* из S Î VN в КС-грамматике G = (VT, VN, P, S), называется левым (левосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого левого нетерминала.

Определение: вывод цепочки b Î (VT)^* из S Î VN в КС-грамматике G = (VT, VN, P, S), называется правым (правосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого правого нетерминала.

В грамматике для одной и той же цепочки может быть несколько выводов, эквивалентных в том смысле, что в них в одних и тех же местах применяются одни и те же правила вывода, но в различном порядке.

Например, для цепочки a+b+a в грамматике

G = ({a,b}, {S,T}, {S ® T | T+S; T ® a|b}, S)

можно построить выводы:

(1) S®T+S®T+T+S®T+T+T®a+T+T®a+b+T®a+b+a

(2) S®T+S®a+S®a+T+S®a+b+S®a+b+T®a+b+a

(3) S®T+S®T+T+S®T+T+T®T+T+a®T+b+a®a+b+a

Здесь (2) - левосторонний вывод, (3) - правосторонний, а (1) не является ни левосторонним, ни правосторонним, но все эти выводы являются эквивалентными в указанном выше смысле.

Для КС-грамматик можно ввести удобное графическое представление вывода, называемое деревом вывода, причем для всех эквивалентных выводов деревья вывода совпадают.

Определение: дерево называется деревом вывода (или деревом разбора) в КС-грамматике G = {VT, VN, P, S), если выполнены следующие условия:

(1) каждая вершина дерева помечена символом из множества (VN È VT È l), при этом корень дерева помечен символом S; листья - символами из (VT È l);

(2) если вершина дерева помечена символом A Î VN, а ее непосредственные потомки - символами a₁, a₂, ... , a_n, где каждое a_i Î (VT È VN), то A ® a₁a₂...a_n - правило вывода в этой грамматике;

(3) если вершина дерева помечена символом A Î VN, а ее единственный непосредственный потомок помечен символом l, то A ® l - правило вывода в этой грамматике.

Пример дерева вывода для цепочки a+b+a в грамматике G на рис.2.1:

Определение: КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка a Î L(G), для которой может быть построено два или более различных деревьев вывода. В противном случае грамматика называется однозначной.

Это утверждение эквивалентно тому, что цепочка a имеет два или более разных левосторонних (или правосторонних) выводов.

Рис.2.1. Дерево вывода для цепочки a+b+a

Определение: язык, порождаемый грамматикой, называется неоднозначным, если он не может быть порожден никакой однозначной грамматикой.

Пример неоднозначной грамматики:

G = ({if, then, else, a, b}, {S}, P, S),

где P = {S ® if b then S else S | if b then S | a}.

В этой грамматике для цепочки if b then if b then a else a можно построить два дерева вывода.

Однако это не означает, что язык L(G) обязательно неоднозначный. Определенная нами неоднозначность - это свойство грамматики, а не языка, т.е. для некоторых неоднозначных грамматик существуют эквивалентные им однозначные грамматики. Если грамматика используется для определения языка программирования, то она должна быть однозначной. В приведенном выше примере разные деревья вывода предполагают соответствие else разным then. Если договориться, что else должно соответствовать ближайшему к нему then, и подправить грамматику G, то неоднозначность будет устранена:

S ® if b then S | if b then S’ else S | a

S’ ® if b then S’ else S’ | a

Проблема, порождает ли данная КС-грамматика однозначный язык(т.е. существует ли эквивалентная ей однозначная грамматика),является алгоритмически неразрешимой.

Преобразования грамматик

В некоторых случаях КС-грамматика может содержать недостижимые и бесплодные символы, которые не участвуют в порождении цепочек языка и поэтому могут быть удалены из грамматики.

Определение: символ A Î VN называется бесплодным в грамматике G = (VT, VN, P, S), если множество { a | a Î VT^*, A Þ a} пусто.

Алгоритм удаления бесплодных символов:

Вход: КС-грамматика G = (VT, VN, P, S).

Выход: КС-грамматика G’ = (VT, VN’, P’, S), не содержащая бесплодных символов, для которой L(G) = L(G’).

Метод:

Рекурсивно строим множества N₀, N₁, ...

1. N₀ = Æ, i = 1.

2. N_i = {A | (A ® a) Î P и a Î (N_i-1 È VT)^*} È N_i-1.

3. Если N_i ¹ N_i-1, то i = i+1 и переходим к шагу 2, иначе VN’ = N_i; P’ состоит из правил множества P, содержащих только символы из VN’ È VT; G’ = (VT, VN’, P’, S).

Определение: символ x Î (VT È VN) называется недостижимым в грамматике G = (VT, VN, P, S), если он не появляется ни в одной сентенциальной форме этой грамматики.

Алгоритм удаления недостижимых символов:

Вход: КС-грамматика G = (VT, VN, P, S)

Выход: КС-грамматика G’ = (VT’, VN’, P’, S), не содержащая недостижимых символов, для которой L(G) = L(G’).

Метод:

1. V₀ = {S}; i = 1.

2. V_i = {x | x Î (VT È VN), (A ® axb) Î P и A Î V_i-1} È V_i-1.

3. Если V_i ¹ V_i-1, то i = i+1 и переходим к шагу 2, иначе VN’ =
V_i Ç VN; VT’ = V_i Ç VT; P’ состоит из правил множества P, содержащих только символы из Vi; G’ = (VT’, VN’, P’, S).

Определение: КС-грамматика G называется приведенной, если в ней нет недостижимых и бесплодных символов.

Алгоритм приведения грамматики:

(1) обнаруживаются и удаляются все бесплодные нетерминалы.

(2) обнаруживаются и удаляются все недостижимые символы.

Удаление символов сопровождается удалением правил вывода, содержащих эти символы.

Замечание: если в этом алгоритме переставить шаги (1) и (2), то не всегда результатом будет приведенная грамматика.

Для описания синтаксиса языков программирования стараются использовать однозначные приведенные КС-грамматики.

Исключение цепных правил

Определение. Правило грамматики вида A ® B, где A,B Î VN, называется цепным.

Утверждение. ДляКС-грамматики G, содержащей цепные правила , можно построить эквивалентную ей грамматику G', не содержащую цепных правил.

Идея доказательства заключается в следующем.

Если грамматика G имеет правила A ® B, B ® C, C ®aX, то такие правила могут быть заменены одним правилом А ® aX, поскольку вывод A ÞB Þ C ÞaX цепочки aX в грамматике G может быть получен в грамматике G' с помощью правила A ® aX.

В общем случае доказательство последнего утверждения можно выполнить так.

Разобьем множество правил P грамматики G на два подмножества P₁ и P₂, включая в P₁ все правила вида A ®B.

Для каждого правила из P₁ найдем множество правил S(A_i), которые строятся так:
если A_i Þ * A_j и в P₂ есть правило A_j ® a , где a - цепочка словаря (VN ÈVT)^*, то в S(A_i) включим правило A_i ® a .

Построим новое множество правил P’ путем объединения правил P₂ и всех построенных множеств S(A_i). Получим грамматику G' = {VN ,VT , P’, S}, которая эквивалентна заданной и не содержит правил вида A ® B.

В качестве примера выполним исключение цепных правил из грамматикиG :

G = ({+,*,(,),a}, {E,T,F}, P={E ® E+T | T, T ® T*F | F, F ® (E) | a}, E).

Вначале разобьем правила грамматики на два подмножества:

P₁ = {E ® T, T ® F} ,

P₂ = {E ® E+T, T ® T*F, F ®(E) | a }

Для каждого правила из P1 построим соответствующее подмножество.

S(E) = { E ®T*F, E ®(E) | a },

S(T) = { T ® (E) | a}

В результате получаем искомое множество правил грамматики без цепных правил в виде:

P2 U S(E) U S(T) = { E ® T+T | T*F | (E) | a, T ® T*F | (E) | a, F ® (E) | a }

Вопрос 7

Преобразование неукорачивающих грамматик

Последний вид рассматриваемых преобразований связан с удалением из грамматики правил с пустой правой частью.

Определение. Правило вида A ® l называется «пустым» (аннулирующим) правилом.

Определение. Грамматика называется неукорачивающей или грамматикой без «пустых» правил, если либо

1)схема грамматики не содержит аннулирующих правил,

2)либо схема грамматики содержит только одно правило вида S ® l, где S - начальный символ грамматики, и символ S не встречается в правых частях остальных правил грамматики.

Для грамматик, содержащих аннулирующие правила, справедливо следующее утверждение.

Утверждение. Для каждой КС-грамматики G', содержащей аннулирующие правила, можно построить эквивалентную ей неукорачивающую грамматику G, такую что L(G')=L(G).

Построение неукорачивающей грамматики приведет к увеличению числа правил заданной грамматики из-за построения дополнительных правил, получаемых в результате исключения нетерминалов аннулирующих правил. Чтобы построить дополнительные правила необходимо выполнить все возможные подстановки пустой цепочки вместо аннулирующего нетерминала во все правила грамматики.

Если же в грамматике есть правило вида S ® l, где S – начальный символ грамматики, и символ S входит в правые части других правил грамматики, то следует ввести новый начальный символ S’ и заменить правило S ® l двумя новыми правилами: S' ® l и S'® S.

В качестве иллюстрации способа построения неукорачивающих грамматик, исключим аннулирующие правила из следующей грамматики:

G ({a,b}, {S}, P = { S ® aSbS, S ® bSaS, S ® l }, S).

Выполняя все возможные замены символа S в первом правиле грамматики, получаем четыре правила вида:

S ® aSbS, S ® abS, S ® aSb, S ® ab .

Поступая аналогично со вторым правилом, имеем:

S ® bSaS, S ® baS, S ® bSa, S ® ba.

Учитывая, что начальный символ, образующий аннулирующее правило, входит в правые части других правил грамматики, заменим правило S ® l правилами вида S' ® l и S' ® S.

Построенная совокупность правил образует множество правил искомой неукорачивающей грамматики.

S' ® S | l

S ® aSbS | abS | aSb | ab | bSaS | baS | bSa | ba

Не нашли, что искали? Воспользуйтесь поиском по сайту: