Понятие о грамматике языка

Вопрос 1

Трансляторы , интерпретаторы и компиляторы

Транслятор может быть интерпретирующего или компилирующего типа. В первом случае его называют интерпретатором входного языка, а во втором – компилятором.

Интерпретатор последовательно читает предложения входного языка, анализирует их и сразу же выполняет, а компилятор не выполняет предложения языка, а строит программу, которая может в дальнейшем быть запущена для получения результата.

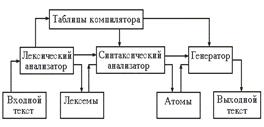
Стадии работы компилятора

Работа компилятора состоит из нескольких стадий, которые могут выполняться последовательно, либо совмещаться по времени. Эти стадии могут быть представлены в виде схемы.

Первая стадия работы компилятора называется лексическим анализом, а программа, её реализующая, - лексическим анализатором (ЛА). На вход лексического анализатора подаётся последовательность символов входного языка. ЛА выделяет в этой последовательности простейшие конструкции языка, которые называют лексическими единицами. Примерами лексических единиц являются идентификаторы, числа, символы операций, служебные слова и т.д. ЛА преобразует исходный текст, заменяя лексические единицы их внутренним представлением – лексемами. Лексема может включать информацию о классе лексической единицы и её значении. Кроме того, для некоторых классов лексических единиц ЛА строит таблицы, например, таблицу идентификаторов, констант, которые используются на последующих стадиях компиляции.

Вторую стадию работы компилятора называют синтаксическим анализом, а соответствующую программу – синтаксическим анализатором(СА). На вход СА подается последовательность лексем, которая преобразуется в промежуточный код, представляющий собой последовательность символов действия или атомов. Каждый атом включает описание операции, которую нужно выполнить, с указанием используемых операндов. При этом последовательность расположения атомов, в отличие от лексем, соответствует порядку выполнения операций, необходимому для получения результата.

На третьей стадии работы компилятора осуществляется построение выходного текста. Программа, реализующая эту стадию, называется генератором выходного текста(Г). Генератор каждому символу действия, поступающему на его вход, ставит в соответствие одну или несколько команд выходного языка. В качестве выходного языка могут быть использованы команды устройства, команды ассемблера, либо операторы какого-либо другого языка.

Рассмотренная схема компилятора является упрощенной, поскольку реальные компиляторы, как правило, включают стадии оптимизации.

Построение компилятора

Для построения компилятора необходимо однозначное и точное задание входного и выходного языков. Такое задание предполагает определение правил построения допустимых конструкций (выражений) языка. Множество таких правил называют синтаксисом языка. Кроме того, задание должно включать описание назначения и смысла каждой конструкции языка. Такое описание называют семантикой языка.

Для построения точных и недвусмысленных описаний применяют метод абстракций, который предполагает выделение наиболее существенных свойств рассматриваемого объекта и опускание свойств, менее значимых для рассматриваемого случая. Например, при построении модели входных языков можно рассматривать входной текст как последовательность символов, построенную по определенным правилам, отвлекаясь от характера начертания символов и их расположения на листе. Математические модели, использующие представление текстов в виде цепочек символов, называют формальными языками и грамматиками.

Вопрос 2

Определение: алфавит - это конечное множество символов. (Термин "символ" имеет достаточно ясный интуитивный смысл и не нуждается в дальнейшем уточнении.)

Например, алфавит A= {a, b, c, +, !} содержит 5 букв, а алфавит B = {00, 01, 10, 11} содержит 4 буквы, каждая из которых состоит из двух символов.

Определение:цепочкой символов в алфавите V называется любая конечная последовательность символов этого алфавита.

Определение: цепочка, которая не содержит ни одного символа, называется пустой цепочкой. Для ее обозначения будем использовать символ l.

Более формально цепочка символов в алфавите V определяется следующим образом:

(1) l - цепочка в алфавите V;

(2) если a - цепочка в алфавите V и a - символ этого алфавита, то aa или аa - цепочка в алфавите V;

(3) b - цепочка в алфавите V тогда и только тогда, когда она является таковой в силу (1) и (2).

Определение: если a и b - цепочки, то цепочка ab называется конкатенацией (или сцеплением) цепочек a и b.

Например, если a = ab и b = cd, то ab = abcd.

Для любой цепочки a всегда al = la = a.

Определение: обращением (или реверсом) цепочки a называется цепочка, символы которой записаны в обратном порядке.

Обращение цепочки a будем обозначать a^R.

Например, если a = abcdef, то a^R = fedcba.

Для пустой цепочки: l = l^R.

Определение:n-ой степенью цепочки a (будем обозначать aⁿ) называется конкатенация n цепочек a.

a⁰ = l; aⁿ = aa^n-1 = a^n-1a.

Определение: длина цепочки - это число составляющих ее символов.

Например, если a = abcdefg, то длина a равна 7.

Длину цепочки a будем обозначать |a|. Длина l равна 0.

Определение: язык в алфавите V - это подмножество цепочек конечной длины в этом алфавите.

Определение: обозначим через V^* множество, содержащее все цепочки в алфавите V, включая пустую цепочку l.

Например, если V={0,1}, то V^* = {l, 0, 1, 00, 11, 01, 10, 000, 001, 011, ...}.

Определение: обозначим через V⁺ множество, содержащее все цепочки в алфавите V, исключая пустую цепочку l.

Следовательно, V^* = V⁺ È {l}.

Ясно, что каждый язык в алфавите V является подмножеством множества V^*.

Известно несколько различных способов описания языков [3]. Один из них использует порождающие грамматики. Именно этот способ описания языков чаще всего будет использоваться нами в дальнейшем.

Определение: декартовым произведением A ´ B множеств A и B называется множество {(a,b) | a Î A, b Î B}.

Цепочкой символов (или строкой) называют произвольную последовательность символов, записанных один за другим. Цепочка – это последовательность, в которую могут входить любые допустимые символы.

Понятие символа (или буквы) является базовым в теории формальных языков и не нуждается в определении.

Цепочки символов обозначают греческими буквами: α, β, γ, …

Цепочка – это необязательно некоторая осмысленная последовательность символов. Последовательность «аввв..аагрьь ,.лл» – пример цепочки символов.

Для цепочки символов важен состав и количество символов в ней, а также порядок символов в цепочке. Один и тот же символ может произвольное число раз входить в цепочку. Поэтому цепочки «а» и «аа», а также «аб» и «ба» – это разные цепочки символов. Цепочки символов α и β равны (совпадают), α = β, если они имеют один и тот же состав символов, одно и то же их количество и одинаковый порядок следования символов в цепочке.

Количество символов в цепочке называют длиной цепочки. Длина цепочки символов α обозначается как |α|. Очевидно, что если α = β, то и |α| = |β|.

Основной операцией над цепочками символов является операция конкатенации (объединения или сложения) цепочек.

Конкатенация (сложение, объединение) двух цепочек символов – это дописывание второй цепочки в конец первой. Конкатенация цепочек α и β обозначается как αβ. Выполнить конкатенацию цепочек просто: например, если α = «аб», а β = «вг», то αβ = «абвг».

Так как в цепочке важен порядок символов, то очевидно, что операция конкатенации не обладает свойством коммутативности, то есть в общем случае существуют α и β такие, что αβ ≠ βα. Также очевидно, что конкатенация обладает свойством ассоциативности, то есть (αβ)γ = α(βγ).

Можно выделить еще две операции над цепочками.

Обращение цепочки – это запись символов цепочки в обратном порядке. Обращение цепочки α обозначается как α^R. Если α = «абвг», то α^R = «гвба». Для операции обращения справедливо следующее равенство ∀α,β: (αβ)^R = β^Rα^R. Т.е. обращение конкатенации равно конкатенации обращений.

Итерация (повторение) цепочки n раз, где n є N,

n > 0 – это конкатенация цепочки самой с собой n раз. Итерация цепочки α n раз обозначается как αⁿ. Для операции повторения справедливо следующее равенство∀ α: α¹ = α, α² = αα, α³ = ααα, … и т.д.

Среди всех цепочек символов выделяется одна особенная – пустая цепочка. Пустая цепочка символов – это цепочка, не содержащая ни одного символа. Пустую цепочку обозначают греческой буквой λ (в литературе ее иногда обозначают латинской буквой е или греческой ε).

Для пустой цепочки справедливы следующие равенства:

1) |λ| = 0 – Длина пустой цепочки; Д

2) ∀α: λα = αλ = α – Коммутативность; К

3) λ^R = λ – Обращение; О

4) ∀ n ≥ 0: λⁿ = λ – Итерация; И

5) ∀ α: α⁰ = λ.

Вопрос3

Понятие о грамматике языка

Грамматика − это описание способа построения предложений некоторого языка. Иными словами, грамматика − это математическая система, определяющая язык.

Фактически, определив грамматику языка, мы указываем правила порождения цепочек символов, принадлежащих этому языку. Таким образом, грамматика − это генератор цепочек языка. Она относится ко второму способу определения языков − порождению цепочек символов.

Грамматику языка можно описать различными способами. Например, грамматика русского языка описывается довольно сложным набором правил, которые изучают в начальной школе. Но для многих языков (и для синтаксической части языков программирования в том числе) допустимо использовать формальное описание грамматики, построенное на основе системы правил (или продукций).

Правило (или продукция) − это упорядоченная пара цепочек символов (α, β). В правилах очень важен порядок цепочек, поэтому их чаще записывают в виде α→β (или α: = β). Такая запись читается как «α порождает β» или «β по определению есть α».

Грамматика языка программирования содержит правила двух типов: первые (определяющие синтаксические конструкции языка) довольно легко поддаются формальному описанию; вторые (определяющие семантические ограничения языка) обычно излагаются в неформальной форме. Поэтому любое описание (или общепринятый стандарт) языка программирования обычно состоит из двух частей: вначале формально излагаются правила построения синтаксических конструкций, а потом на естественном языке дается описание семантических правил.

Язык, заданный грамматикой G, обозначается как L(G).

Две грамматики G и G' называются эквивалентными, если они определяют один и тот же язык: L(G) = L(G'). Две грамматики G и G' называются почти эквивалентными, если заданные ими языки различаются не более чем на пустую цепочку символов: L(G) U {λ} = L(G') U {λ}.

Вопрос 4

Определение: порождающая грамматика G - это четверка (VT, VN, P, S), где

VT - алфавит терминальных символов (терминалов),

VN - алфавит нетерминальных символов (нетерминалов), не пересекающийся с VT,

P - конечное подмножество множества (VT È VN)⁺ ´ (VT È VN)^*; элемент (a, b) множества P называется правилом вывода и записывается в виде a ® b,

S - начальный символ (цель) грамматики, S Î VN.

Для записи правил вывода с одинаковыми левыми частями

a ® b_1, a ® b_2, ..., a ® b_n

будем пользоваться сокращенной записью

a ® b₁ | b₂ |...| b_n.

Каждое b_i , i= 1, 2, ... ,n , будем называть альтернативой правила вывода из цепочки a.

Пример грамматики:

G1 = ({0,1}, {A,S}, P, S),

где P состоит из правил

S ® 0A1

0A ® 00A1

A ® l

Определение: цепочка b Î (VT È VN)^* непосредственно выводима из цепочки a Î (VT È VN)⁺ в грамматике G = (VT, VN, P, S) (обозначим a ® b), если a = x₁gx₂, b = x₁dx₂, где x₁, x₂, d Î (VT È VN)^*, g Î (VT È VN)⁺ и правило вывода g ® d содержится в P.

Например, цепочка 00A11 непосредственно выводима из 0A1 в грамматике G1.

Определение: цепочка b Î (VT È VN)^* выводима из цепочки a Î (VT È VN)⁺ в грамматике G = (VT, VN, P, S) (обозначим a Þ b), если существуют цепочки g₀, g₁, ... , g_n (n³0), такие, что a = g₀ ® g₁ ® ... ® g_n= b.

Определение: последовательность g₀, g₁, ... , g_n называется выводом длины n.

Например, S Þ 000A111 в грамматике G1 (см. пример выше), т.к. существует вывод S ® 0A1 ® 00A11 ® 000A111. Длина вывода равна 3.

Определение: языком, порождаемым грамматикой G = (VT, VN, P, S), называется множество L(G)={a Î VT^* | S Þ a}.

Другими словами, L(G) - это все цепочки в алфавите VT, которые выводимы из S с помощью P.

Например, L(G1) = {0ⁿ1ⁿ | n>0}.

Определение: цепочка a Î (VT È VN)^*, для которой S Þ a, называется сентенциальной формой в грамматике G = (VT, VN, P, S).

Таким образом, язык, порождаемый грамматикой, можно определить как множество терминальных сентенциальных форм.

Определение: грамматики G1 и G2 называются эквивалентными, если L(G1) = L(G2).

Например, G1 = ({0,1}, {A,S}, P1, S) и G2 = ({0,1}, {S}, P2, S), где

P1: S ® 0A1 P2: S ® 0S1 | 01

0A ® 00A1

A ® l

эквивалентны, т.к. обе порождают язык

L(G1) = L(G2) = {0ⁿ1ⁿ | n>0}.

Определение: грамматики G1 и G2 почти эквивалентны, если
L(G1) È {l} = L(G2) È {l}.

Другими словами, грамматики почти эквивалентны, если языки, ими порождаемые, отличаются не более, чем на l.

Например, G1 = ({0,1}, {A,S}, P1, S) и G2 = ({0,1}, {S}, P2, S), где

P1: S ® 0A1 P2: S ® 0S1 | l

0A ® 00A1

A ® l

почти эквивалентны, т.к. L(G1)={0ⁿ1ⁿ | n>0}, а L(G2)={0ⁿ1ⁿ | n³0}, т.е. L(G2) состоит из всех цепочек языка L(G1) и пустой цепочки, которая в L(G1) не входит.

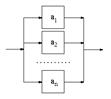
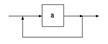
Вопрос 4

Способы задания схем грамматик

Схема грамматики содержит правила вывода, определяющие синтаксис языка, или, другими словами, структуру цепочек порождаемого языка. Для задания правил используются различные формы описания: символическая, форма Бэкуса-Наура, итерационная форма и синтаксические диаграммы.

При рассмотрении общих свойств грамматик обычно применяют символическую форму задания правил. Эта форма была рассмотрена в предыдущем параграфе.

В практических применениях вместо символического представления схем грамматик обычно используют форму Бэкуса-Наура, или синтаксические диаграммы.

Форма Бэкуса -Наура

При описании синтаксиса конкретных языков программирования приходится вводить большое число нетерминальных символов, и символическая форма записи теряет свою наглядность. В этом случае применяют форму Бэкуса-Наура (БНФ), которая предполагает использование в качестве нетерминальных символов комбинаций слов естественного языка, заключенных в угловые скобки, а в качестве разделителя - специального знака, состоящего из двух двоеточий и равенства. Например, если правила L  ®  EL и L ®  Eзаписаны в символической форме, и символ Lсоответствует синтаксическому понятию "список", а символ E - "элемент списка", то их можно представить в форме Бэкуса-Наура так:

<список> ::= <элемент списка><список>,
<список> ::= <элемент списка>.

Чтобы сократить описание схемы грамматики, в БНФ разрешается объединять правила c одинаковой левой частью в одно правило, правая часть которого должна включать правые части объединяемых правил, разделенные вертикальной чертой. Используя объединение правил, для рассматриваемого примера получаем:

<список>::=<элемент списка><список>|<элемент списка>.

Итерационная форма

Для получения более компактных описаний синтаксиса применяют итерационную форму описания. Она предполагает введение специальной операции, которая называется итерацией и обозначается парой фигурных скобок со звездочкой. Итерация вида {a}^* определяется как множество, включающее цепочки всевозможной длины, построенные с использованием символа a, и пустую цепочку.

{a}^* = {l, a, aa, aaa, aaaa,...}.

Используя итерацию для описания множества цепочек, задаваемых символическими правилами, для списка получаем:

L ® E { E }*

Например, описание множества цепочек, каждая из которых должна начинаться знаком # и может состоять из произвольного числа букв x и y, может быть представлено в итерационной форме так:

I ® #{x | y}^*

В итерационных формах описания наряду с итерационными cкобками часто применяют квадратные скобки для указания того, что цепочка , заключенная в них, может быть опущена. С помощью таких скобок правила:

A®x A y B z и A®x B z

могут быть записаны так:

A®x [ A y ] B z

Синтаксические диаграммы

Для того, чтобы улучшить зрительное восприятие и облегчить понимание сложных синтаксических описаний, применяют представление правил грамматики в виде синтаксических диаграмм. Правила построения таких диаграмм можно сформулировать в следующем виде:

1)Каждому правилу вида A ® a₁ | a₂ |...| a_k ставится в соответствие диаграмма, структура которой определяется правой частью правила.

2)Каждое появление терминального символа xв цепочке a_i изображается на диаграмме дугой, помеченной этим символом x, заключенным в кружок .

3) Каждому появлению нетерминального символа <A> в цепочке a_i ставится в соответствие на диаграмме дуга, помеченная символом, заключённым в квадрат .

4) Порождающее правило, имеющее вид:

A ® a₁a₂...a_n

изображается на диаграмме следующим образом:

5) Порождающее правило, имеющее вид:

A ® a₁ | a₂ | ... | a_n

изображается на диаграмме так:

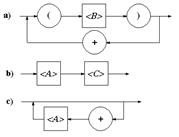
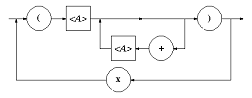
6) Если порождающее правило задано в виде итерации:

A ® {a}*,

то ему соответствует диаграмма:

Число синтаксических диаграмм, которые можно построить для заданной схемы грамматики, определяется числом правил. Чтобы сократить число диаграмм, их объединяют, заменяя нетерминальные символы, входящие в диаграмму, построенными для них диаграммами.

Правила 3-6 предусматривают, что в качестве цепочки a1 на объединенной диаграмме могут быть использованы диаграммы построенные для этих цепочек. В качестве примера рассмотрим грамматику G3 с начальным символом A :

G3: ({ x, +, (, ) }, {<A>, <B>, <C>}, P = { A ® x | (B), B ® AC, C ® {+A}* }, S).

Синтаксические диаграммы для такой грамматики имеют вид:

Заменяя нетерминальные символы, соответствующими диаграммами, получаем объединенную диаграмму в виде:

Вопрос 5

Не нашли, что искали? Воспользуйтесь поиском по сайту: