Приложение 1. Справочная система MATLAB

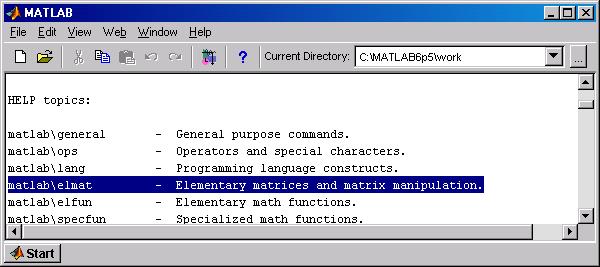
Среда MATLAB обладает многоуровневой справочной системой, которая позволяет получить информацию как по самой MATLAB, так и по всем ее приложениям.

Получить доступ к справочной информации MATLAB можно различными способами: введя в командную строку соответствующую справочную команду или функцию; с помощью команд меню Help; щелкнув на кнопке со знаком вопроса на панели инструментов основного окна MATLAB.

MATLAB имеет интерактивную справочную систему, которая реализуется в командном режиме с помощью ряда команд. Одной из них является команда

>> help

которая выводит весь список папок (каталогов), содержащих m-файлы с определениями операторов, функций и иных объектов (рис. П.1). Этот список дает представление о пакетах прикладных программ, расширяющих возможности системы MATLAB и содержащих примеры применения системы.

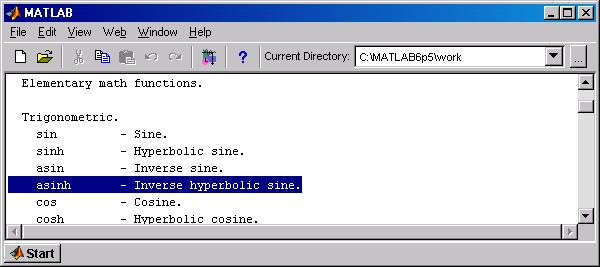
Рис. П.1

При вводе команды

>> help elfun

в командное окно выводится список встроенных элементарных функций (рис.П.2).

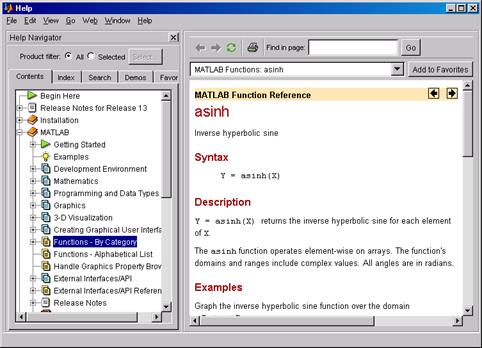
Рис. П.2

Для получения справочной информации по любой из них требуется выполнить команду help <имя функции>, например

>> help asinh

ASINH Inverse hyperbolic sine.

ASINH(X) is the inverse hyperbolic sine of the elements of X.

Overloaded methods

help sym/asinh.m

Теперь полученное сообщение содержит информацию о функции asinh. Хотя имя функции в MATLAB задается малыми (строчными) буквами, в сообщениях справочной системы имена функций и команд выделяются большими (прописными) буквами.

Если в командной строке набрать команду doc elfun, то при этом перейдем в главное окно Help внутренней справочной системы MATLAB, в правой половине которого будет открыта первая страница документа справочной информации с указанным заголовком.

Для получения справки по конретной функции необходимо выбрать вкладку с одноименным названием и щелкнуть на ней левой кнопкой мыши. Для получения более полной информации, снабженной графиками и лучше отформатированной, надо выполнить команду doc <имя функции>, например (рис. П.3)

>> doc asinh

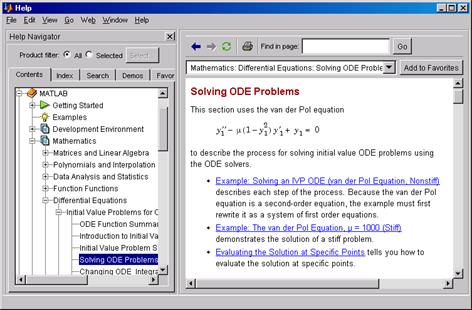
Рис. П.3

Кнопка вызова ? окна Help вынесена на панель инструментов главного окна рабочей среды.

В главном окне Help внутренней внутренней справочной системы MATLAB слева находится панель Help Navigator, так называемый Help - навигатор с пятью вкладками, на которых реализованы различные способы поиска информации:

Contents (Cодержание) – поиск информации по оглавлению доступных разделов;

Index (Индекс) – поиск информации по алфавитному каталогу;

Search (Поиск) – поиск информации по ключевому слову или фразе, набираемых в поле ввода;

Demos (Примеры) – переход к странице, с которой можно получить доступ к демонстрационным примерам по любым темам;

Favorites (Фавориты) – список разделов, выделенных пользователем в качестве наиболее посещаемых.

При вызове окна справки Help по умолчанию в нем отображается вкладка Contents с оглавлением, представленным в виде дерева справочных каталогов (разделов). Чтобы раскрыть в оглавлении нужный раздел, щелкните по кнопке со знаком <+> (слева от названия раздела) либо дважды щелкните по кнопке с его названием.

Каждый раздел имеет подраздел Getting Started (Начало), который кратко знакомит с содержимым этого раздела, а также подраздел Examples (Примеры), помеченный пиктограммой с изображением лампочки (здесь можно найти соответствующие данной теме примеры).

Далее можно перейти к требуемому подразделу.

В разделе 6.6 рассмотрен пример решения с помощью солвера ode45 задачи Коши для обыкновенного дифференциального уравнения. Там же упоминалось уравнение Ван-дер-Поля y'' - μ(1 - y²)y'+y = 0, пример решения которого с помощью солвера ode15sможно найти во встроенной в пакет MATLAB справочной системе Help. Это решение приведено внутри раздела Differential Equations, являющегося подразделом раздела Mathematics (рис. П.4).

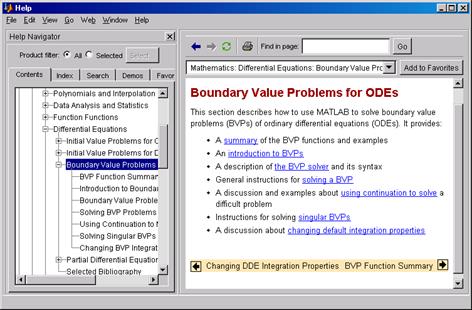
Рис.П.4

Система MATLAB предлагает и решатели для граничных задач, а также решатели для дифференциальных уравнений с частными производными (рис. П.5).

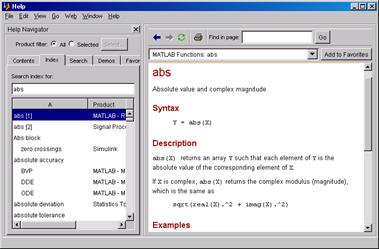
Рис.П.5

Из рис. П.5 видно, что нужно ознакомится с разделами Boundary Value Problems for ODEs (Граничные задачи для обыкновенных дифференциальных уравнений) и Partial Differential Equations (Дифференциальные уравнения в частных производных). Они находятся внутри раздела Differential Equations, являющегося подразделом раздела Mathematics. Решению дифференциальных уравнений в частных производных посвящен отдельный пакет расширенной системы MATLAB – Partial Differentional Equation ToolBox.

Чтобы выделить больше места для отображения справочной информации, панель Help Navigator можно закрыть щелчком по кнопке с крестиком в правом верхнем углу. Открыть панель после этого можно щелчком по кнопке ?.

Вкладка Index (рис. П.6) позволяет

Рис. П.6

организовать поиск по ключевому слову, набираемому в поле ввода под надписью Search index for (Поиск по индексу). Имеется возможность перемещаться по упорядоченному списку либо с помощью линейки прокрутки, либо набрав в поле ввода одну или несколько начальных букв.

Вкладка Search (рис. П.7) позволяет организовать несколько вариантов поиска в зависимости от того, что выбрано среди строк раскрывающегося списка Search type (Тип поиска). Вариантов всего четыре: поиск по всем документам Full text (Полный текст); поиск по заголовкам документов Docment Titles (Название документа); поиск по именам функций Function name (Имя функции); поиск в базе данных по каналам Интернета Online Knowledge Base (Информационная база в Интернете).

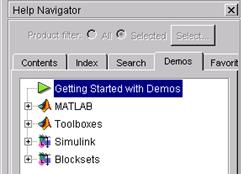
Рис. П.7

Вкладка Demos (рис. П.8) содержит на левой панели дерево каталогов с

демонстрационными примерами. Открыв нужный каталог (щелчком на кнопке со знаком <+>), попадаем на страницу со списком примеров по выбранной теме.

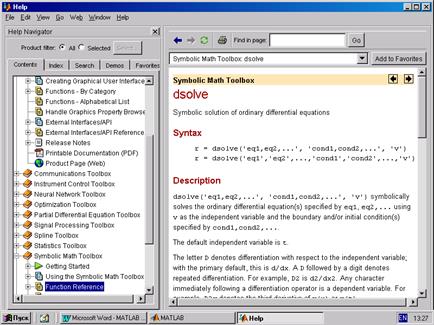
Рис. П.8

Примеры могут содержать листинги программ MATLAB, которые можно просмотреть и запустить на выполнение. Для запуска примера нужно щелкнуть на кнопке Run this demo (Запустить этот пример) внизу страницы с примером.

Примеры могут представлять собой видеоролики или видеоуроки, демонстрирующие, как пользоваться тем или иным инструментом.

Страницы, которые просматриваются чаще всего, можно добавить в список избранных с помощью команды Add to Favorites (Добавить в избранное). После этого их названия появятся в меню Favorites, откуда их можно будет быстро открыть.

Использование команд справки является быстрым способом получения информации, если вы точно знаете, что ищете и как это называется.

Например: doc ops – выводит информацию по разделу операторов и специальных символов; doc function – выводит информацию о назначении и создании файл-функций.

Для ускорения поиска сведений о функциях в файлах помощи предусмотрены два систематизированных каталога: список функций, упорядоченных по алфавиту и классифицированных по категориям MATLABFunction Listed by Category (Список функций MATLAB по категориям)) и общий список всех функций, упорядоченных по алфавиту MATLABFunction Listed Alphabetically(Алфавитный список функций MATLAB).

Справочная система MATLAB позволяет получить информацию по пакету Symbolic Math Toolbox как по одному из приложений MATLAB. Для этого после вызова главного окна справки Help в оглавлении вкладки Contents надо раскрыть раздел Symbolic Math Toolbox. Способы получения информации по пакету в окне справки Help аналогичны тем, что были показаны выше при поиске информации по самой MATLAB.

В интерактивной справочной системе MATLAB с помощью команды

>>help symbolic

можно получить перечень входящих в пакет Symbolic Math Toolbox команд и функций. Для получения справки по любой команде или функции можно использовать команду

>>help sym/name.m,

где name – это имя соответствующей команды или функции, а name.m – имя m-файла, задающего данную команду или функцию. Вместо help можно использовать doc. При этом перейдем в главное окно Help внутренней справочной системы MATLAB, в правой половине которого будет открыта первая страница документа справочной информации с указанным заголовком (рис. П.9):

>> doc dsolve

Рис. П.9

Для получения списка функций системы Maple, доступных из МАТLAB, служит команда mfunlist. Для доступа к информации по любой функции Maple, в том числе и не входящей в список команды mfunlist, предназначена команда mhelp <имя функции>.

Не нашли, что искали? Воспользуйтесь поиском по сайту: