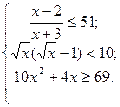Интерполяционный полином Лагранжа

Предположим, что некоторая функция f(x) задана таблицей своих значений:

Требуется найти интерполяционный полином Лагранжа – многочлен L_n(x) степени не выше n, значения которого в точках x_k совпадают со значениями данной функции в этих точках, т.е. L_n(x_k) = y_k, k = 0,…, n.

Для нахождения интерполяционного полинома Лагранжа в Maple служит команда interp.

Пример:

Найти интерполяционный полином Лагранжа функции f(x)

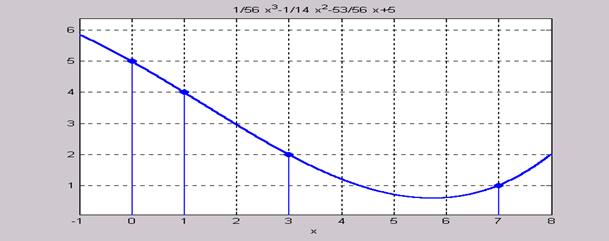
Решение:

>> syms x

>> maple('interp([0,1,3,7],[5,4,2,1],x)')

ans =

1/56*x^3-1/14*x^2-53/56*x+5

Построим на рис. 7.7 узлы интерполяции (команда stem) и график найденного интерполяционного полинома Лагранжа

L₃(x) = x³ - x² - x+5:

>> stem([0 1 3 7],[5 4 2 1],'fill')

>> hold

Current plot held

>> ezplot(ans,-1, 8)

>>grid

Рис. 7.7

Как видим из рис. 7.7, график найденного интерполяционного полинома Лагранжа проходит через узлы интерполирования

Решение неравенств и систем неравенств

Для решения неравенств и систем неравенств в Maple служит команда solve.

Пример:

Решить неравенство

> 2.

Решение:

>> maple('solve((x-2)/(x+3)>2,{x})')

ans =

{-8 < x, x < -3}

Значит, - 8 < x < - 3 – решение неравенства.

Пример:

Решить систему неравенств

Решение:

>> maple('solve({(x-2)/(x+3)<=51,sqrt(x)*(sqrt(x)-1)<10,10*x^2+4*x>=69},x)')

ans =

{RootOf(-69+10*_Z^2+4*_Z,2.4343879744638981326796776750121) <= x, x < RootOf(-21*_Z+_Z^2+100,13.701562118716424343244108837311)}

>> vpa(ans,4)

ans =

{2.434 <= x, x < 13.70}

Таким образом, 2,434 ≤ x < 13,70 – приближенное решение системы неравенств (с точностью до 4 - х значащих цифр). Точное решение имеет вид

≤ x < .

Разложение в ряд Тейлора функции нескольких переменных

Для получения разложений аналитических функций нескольких переменных в ряд Тейлора (и Маклорена) в Maple служит команда mtaylor.

Пример:

Разложить функцию f(x,y) = sin(x²+y²) в ряд Маклорена (по степеням x, y) до 8 - й степени.

Решение:

>> maple('readlib(mtaylor):mtaylor(sin(x^2+y^2),[x,y],8)')

ans =

x^2+y^2-1/6*x^6-1/2*y^2*x^4-1/2*y^4*x^2-1/6*y^6

Пример:

Найти разложение функции f(x,y) = sin(x²+y²) в ряд Тейлора по степеням x - 1, y до 3 - й степени.

Решение:

>> maple('readlib(mtaylor):mtaylor(sin(x^2+y^2),[x=1,y],3)')

ans =

sin(1)+2*cos(1)*(x-1)+(-2*sin(1)+cos(1))*(x-1)^2+cos(1)*y^2

Решение дифференциальных уравнений с помощью степенных рядов

Пример:

Решить дифференциальное уравнение y' = cosx+e^y с начальным условием y(0) = 1.

Решение:

Обращение к dsolve возвращает сообщение о том, что решение не найдено:

>> dsolve('Dy=cos(x)+exp(y)','y(0)=1','x')

ans =

[ empty sym ]

Команда dsolve не нашла аналитического решения в MATLAB. Известно, что решения этого дифференциального уравнения в аналитическом виде не существует. Найти разложение решения в степенной ряд (до 6-й степени по умолчанию) можно с помощью команды dsolve системы Maple.

>> maple('dsolve({diff(y(x),x)=cos(x)+exp(y(x)),y(0)=1},y(x),series)')

ans =

y(x) = series(1+(1+exp(1))*x+(1/2*exp(1)*(1+exp(1)))*x^2+(-1/6+1/3*exp(1)*(3/2*exp(1)+exp(1)^2+1/2))*x^3+(1/2*exp(1)^3+1/4*exp(1)^4+7/24*exp(1)^2)*x^4+(1/2*exp(1)^4+1/5*exp(1)^5+5/12*exp(1)^3+1/120-1/40*exp(1)+1/12*exp(1)^2)*x^5+O(x^6),x,6)

Имеется возможность управлять порядком разложения. Найдем разложение решения в степенной ряд до 3 -й степени:

>> maple('Order:=3;dsolve({diff(y(x),x)=cos(x)+exp(y(x)),y(0)=1},y(x),series)')

ans =

Order := 3y(x) = series(1+(1+exp(1))*x+(1/2*exp(1)*(1+exp(1)))*x^2+O(x^3),x,3)

Решение тригонометрических уравнений

Пример:

Решить тригонометрическое уравнение cos2x+ sinx = 1.

Решение:

Обращение к solve приводит к следующим решениям:

>> syms x

>> solve('cos(2*x)+sin(x)=1',x)

ans =

[ 0]

[ pi]

[ 1/6*pi]

[ 5/6*pi]

Отметим, что непосредственно в MATLAB команда solve возвращает только значения корней, которые находятся в интервале [-p;p]. Для получения всех решений тригонометрического уравнения cos2x+ sinx = 1 следует использовать следующие команды системы Maple:

>> maple('_EnvAllSolutions:=true');

>> maple('solve(cos(2*x)+sin(x)=1,x)')

ans =

2*pi*_Z, pi+2*pi*_Z, 1/6*pi+2*pi*_Z, 5/6*pi+2*pi*_Z

Здесь _Z – переменная целого типа.

Вопросы для самопроверки

1. Как создать символьную переменную в MATLAB?

2. Как в MATLAB осуществляется управление точностью вычислений?

3. Как выполняются в MATLABупрощения и подстановки в символьных выражениях?

4. Как в MATLAB вычислить в символьном виде значение предела функции?

5. Как выполнить в MATLABдифференцирование в символьном виде?

6. Как вычислить в MATLABзначение интеграла в символьном виде?

7. Как получить в MATLABв символьном виде разложение функции в ряд?

8. Как вычислить в MATLABзначение суммы и произведения ряда в символьном виде?

9. Как можно в MATLAB найти решение алгебраического уравнения в символьном виде?

10. Как можно в MATLAB найти решение дифференциального уравнения в символьном виде?

11. Как осуществляется в MATLAB в символьном виде прямое и обратное преобразование Лапласа?

12. Перечислите встроенные в MATLAB средства визуализации символьных вычислений?

13. Как можно в MATLAB обратится к ядру системы Maple?

ПРИЛОЖЕНИЯ

Не нашли, что искали? Воспользуйтесь поиском по сайту: