Графики с указанием погрешности

Если при измерении значений функции имеется существенная погрешность, которая часто бывает случайной величиной, то для построения графика с учетом погрешности может быть использована команда errorbar(…). Эта команда позволяет визуально оценить погрешность в каждой точке измерения путем представления ее в виде буквы I. При этом высота буквы I равна удвоенному значению погрешности измерения ординаты функции y(t)в каждой точке.

errorbar(y,t,k,u) –строит график значений функции yв зависимости от значений аргумента t с указанием нижней kи верхней uграниц погрешности. Значения kи u могут быть заданы в виде последовательности как детерминированных, так и случайных чисел.

errorbar(y,t,E) –строит график значений функции yв зависимости от значений аргумента t с указанием границ погрешности в виде [y-E; y+E].

errorbar(…,S) –строит график значений функции yв зависимости от значений аргумента t по одному из указанных выше вариантов, но с применением дополнительного параметра S, который используется по тем же правилам, что и ранее.

Пример 11. С помощью команды errorbar(y,t,E,S)построить график функции y(t) = e^0,05t, где аргумент tменяется от -2,91 до 55,2 с шагом 2,1 (рис. 5.13). Параметр Еявляется последовательностью случайных чисел, которая задается с помощью встроенных функций MATLAB,т. е. randи size (напомним, что rand генерирует последовательность равномерно распределенных случайных чисел, аsizeопределяетразмер массива сгенерированных чисел). Параметр E задать в видеE = rand(size(4.7*t)).Описание дополнительного параметра S: цвет – зеленый, тип маркера – треугольник вершиной к верху, стиль лини – пунктирная ( табл. 5.1).

>> t=[-2.91:2.1:55.2];

>> y=exp(0.05*t);

>> E=rand(size(4.7*t));

>> errorbar(t,y,E,'g^:')

Рис. 5.13

Графики в логарифмическом и полулогарифмическом масштабах

Встречаются случаи, когда диапазон изменения функции настолько велик, что для ее графической визуализации приходится применять логарифмический масштаб. Для построения графиков в логарифмическом и полулогарифмическом масштабе служат следующие команды:

loglog(…)– логарифмический масштаб по обеим осям;

semilogx(…)– логарифмический масштаб по оси абсцисс;

semilogy(…)– логарифмический масштаб по оси ординат.

Аргументы этих команд (все, что стоит внутри скобок) формируются по тем же правилам, что и в команде plot(…).

Пример 12. Построить в одном окне в полулогарифмическом масштабе с использованием команды semilogx(…) графики зависимостей f(t) = t·log(t²)+1000и g(t) = 10·t·sin(log(t²))(рис. 5.14)при условии, что tменяется на интервале [10;1000] с шагом 1. График функции g(t)выделить красным цветом.

>> t=[10:1000];

>> f=t.*log(t.^2)+1000;

>> g=10*t.*sin(log(t.^2));

>> semilogx(t,f,t,g,'r')

Рис. 5.14

Графики параметрических функций

Напомним, как образуется график параметрической функции.

Если имеются две функции x(t)и y(t),то параметрическая функция задается в виде y(x). Таким образом, для построения графика такой функции следует:

задать пределы и шаг изменения аргумента t;

вычислить значения функций x(t)и y(t);

использовать команду plot(…)в одном из ее вариантов.

Пример 13. Используя в качестве исходных функций x(t) = sin(t)и y(t) = 0,1·cos(t),построить график (рис. 5.15) параметрической функции y(x) при условии, что tизменяется на интервале [0;2π] с шагом 0,01.

Вариант 1 Вариант 2

t=[0:0.01:2*pi]; t=[0:0.01:2*pi];

x=sin(t); plot(sin(t), 0.1*cos(t))

y=0.1*cos(t);

plot(x,y)

Рис. 5.15

На этом мы завершим рассмотрение 2D графики.

Дополнительно отметим, что выше рассмотрены лишь основы графической визуализации на плоскости. На самом деле графические возможности среды MATLAB значительно шире.

D графика

Под 3D графикой будем понимать построение графической зависимости функции двух переменных z(x,y). График такой функции представляет собой изображение некоторой поверхности в трехмерном пространстве и строится с использованием аксонометрического метода.

Для графической визуализации функции двух переменных следует:

а) сформировать матрицу [x;y] с координатами узлов сетки на прямоугольной области определения функции. Матрица с координатами узлов сетки генерируется с помощью команды meshgrid(x,y). Аргументами xи yявляются векторы, элементы которых задают координаты узлов прямоугольной сетки. Если область определения функции – квадрат, то в meshgrid(…) можно задать интервал и шаг изменения лишь одного из аргументов функции:

б) вычислить значения функции в узлах сетки;

в) использовать для вывода графика одну из графических команд MATLAB;

г) используя команды оформления графика, нанести дополнительную информацию.

Как и прежде, главным условием для отображения графических зависимостей функции z(x,y) является понимание того, как в среде MATLAB осуществляются поэлементные операции с векторами и матрицами.

Линейчатые поверхности

Для построения линейчатых поверхностей используются команды plot3(…)и contour3(…).

Пример 14. Построить график функции z(x,y) = x+y³ (рис. 5.16),где переменные xи yизменяются на интервале [-8;8] с шагом 0,5. Для построения графика использовать непрерывные линии черного цвета.

>> [x,y]=meshgrid(-8:0.5:8);

>> z=x+y.^3;

>> plot3(x,y,z,’k’)

Обсудим построенный график.

а) Как видно из условия задачи, область определения функции zпредставляет собой квадрат. Поэтому в команде meshgrid(…)указаны пределы и шаг изменения только одного из аргументов функции.

б) Команда meshgrid(…)лишь подготавливает матрицу [x,y], но не выводит ее на экран монитора.

в) В команде plot3(…)присутствует дополнительный параметр, который заключен в апострофы и определяет цвет линий на графике.

г) Все точки каждой из линий, с помощью которых построен график, находятся на одинаковом расстоянии от плоскости zOy. На языке начертательной геометрии они носят название линий профильного уровня.

Следует отметить, что правила применения команды plot3(…) аналогичны правилам применения команды plot(…)в 2D графике.

Рис. 5.16

Используем теперь для построения линейчатой поверхности команду contour3(…).

Пример 15. С использованием команды contour3(…)построить линейчатую поверхность функции z = x²+y² (рис. 5.17).Переменные xиyизменяются на интервале [–3;3] с шагом 0,1. Количество линий на графике 40.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=x.^2+y.^2;

>> contour3 (x,y,z,40)

>> colormap (bone)

>> colorbar

Из рис. 5.17 видно, что линии, с помощью которых построена поверхность, параллельны плоскости xOy. На языке начертательной геометрии они носят название линий горизонтального уровня.

Использование команд colormapи colorbarв приведенном листинге будет пояснено ниже.

Команда contour3(…)можетбыть использован без указания количества линий горизонтального уровня. В этом случае MATLABсамостоятельноопределяет их количество.

Рис. 5.17

Каркасные поверхности

Команда plot3(…) может быть использован для построения так называемой каркасной поверхности, которая ограничивает поверхность геометрического тела и похожа на каркас, сплетенный из проволоки.

Пример 16. Построить график каркасной поверхности функции z(x,y) = x+y³ (рис. 5.18),где переменные xи yизменяются на интервале [–8;8] с шагом 1. Для построения графика использовать непрерывные линии. Линии, расположенные параллельно плоскости zOy, закрасить в черный цвет, а линии, параллельные плоскости zOx – в красный цвет. На плоскостях xOy, zOx,zOyсформировать сетку.

>> [x,y]=meshgrid(-8:8);

>> z=x+y.^3;

>> plot3(x,y,z,'k',y,x,z,'r')

>> grid on

Как видно из текста программы, для формирования каркасной поверхности в команде plot3(…)использованы два аргумента с дополнительными параметрами. При этом во втором аргументе переменные xи yпереставлены местами. Сетка, как и в 2D графике, задается командой grid on.

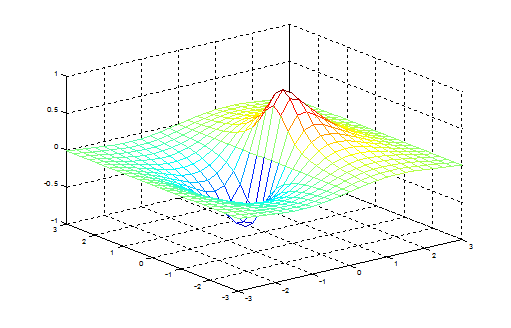
Рис. 5.18

В примере 16 для построения каркасной поверхности была использована команда plot3(…). Однако для построения таких поверхностей в MATLAB имеются и другие команды, например, mesh(…) и surf(…).

Пример 17. С помощью команды mesh(…)построитькаркасную поверхность (рис. 5.18), заданную функцией z = sin(x)/(x²+y2+0,3), где переменные xи yизменяются на интервале [–3;3] с шагом 0,1.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=sin(x)./(x.^2+y.^2+0.3);

>> mesh(x,y,z)

На экране цветного монитора можно видеть, что цвет линий каркасной поверхности зависит от величины значений функцииz. Кроме того, команда mesh(…) предполагает вывод только видимой части поверхности.

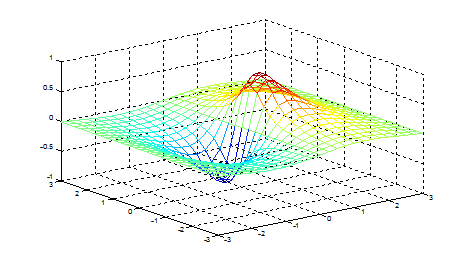
Рис. 5.19

Для того чтобы сделать каркасную поверхность «прозрачной» (рис. 5.20), следует использовать команду hidden off. Предыдущая программа в этом случае имеет вид

>> [x,y]=meshgrid(-3:0.1:3);

>> z=sin(x)./(x.^2+y.^2+0.3);

>> mesh(x,y,z)

>> hidden off

Рис. 5.20

Команда hidden on убирает невидимую часть поверхности, возвращая графику прежний вид.

В отличие от команды mesh(…) применение команды surf(…) позволяет окрасить не только линии графика, но и залить определенным цветом каждую клетку поверхности. Цвет зависит от значений функции в точках, соответствующих углам клетки.

Результат замены команды mesh(x,y,z) в примере 17 на команду surf(x,y,z) представлен на рис. 5.21.

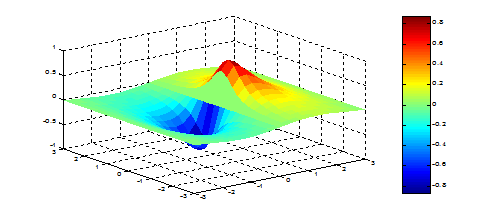
Рис. 5.21

Трехмерные графики, изображенные на рис. 5.19 – 5.21, позволяют наглядно представить форму поверхности, однако по ним трудно судить о значениях двухмерной функции. Для того чтобы частично устранить этот недостаток, можно после команды surf(x,y,z)применить команду colorbar, которая выводит рядом с графиком столбик, устанавливающий соответствие между цветом поверхности и величиной функции. Рис. 5.22 иллюстрирует получающийся результат.

Рис. 5.22

Командуcolorbar можно использовать в сочетании со всеми операторами MATLAB, строящими трехмерные объекты.

Применение после команды surf(x,y,z)команды shading flatпозволяет убрать каркасные линии (рис. 5.23), а использование команды shading interp– получить поверхность, плавно залитую цветом, зависящим от значений функции.

Рис. 5.23

Контурные графики

Контурные графики, как правило, представляют собой некоторый набор линий на плоскости. Каждая из линий является горизонтальной проекцией линии пересечения заданной поверхности с плоскостью горизонтального уровня.

MATLAB позволяет получить различные типы контурных графиков при помощи команд contour(…)и contourf(…).

Пример 18. Построить контурный график функции z = x²+y² (рис. 5.24) из 20 линий. Переменные xиyизменяются на интервале [–3;3] с шагом 0,1.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=x.^2+y.^2;

>> contour (x,y,z,20)

>> colorbar

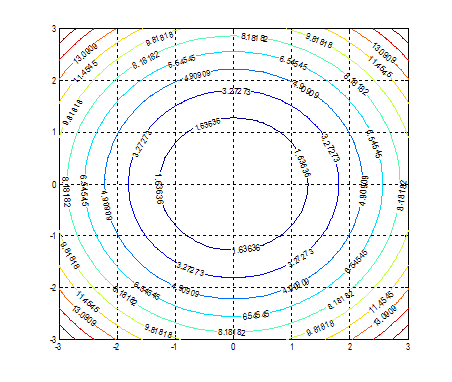
Рис. 5.24

Такой контурный график дает весьма приблизительное представление о том, какое значении функции соответствует той или иной линии уровня.

MATLAB позволяет нанести на каждую линию уровня, значение, которое принимает на ней исследуемая функция. Для этого служит команда clabel (…).

Команда clabel(…) вызывается с двумя аргументами: матрицей, содержащей информацию о линиях уровня, и указателем на график, где следует нанести числовое значение функции.

Пользователю необязательно самому создавать аргументы clabel (…). Для этого команду contour(…)следует вызвать с двумя выходными аргументами.

Поясним это на примере.

Пример 19. Построить контурный график функции z = x²+y² (рис. 5.25), состоящий из 10 оцифрованных линий уровня.Переменные xиyизменяются на интервале [–3;3] с шагом 0,1.

>> [x,y]=meshgrid(-3:0.1:3);

>> z=x.^2+y.^2;

>> [C,H]=contour (x,y,z,10);

>> clabel(C,H)

>> grid on

Рис. 5.25

MATLABпредоставляет возможность оцифровки линий уровня вручную. Для этого вместо команды clabel(C,H)необходимо использоватькоманду clabel(C,H,’manual’). Такая замена в примере 19 приводит к тому, что на экран монитора выводится контурный график без оцифровки линий уровня, но с перекрестьем, которое можно двигать по изображению с помощью мыши. Расположив перекрестье на требуемой линии уровня и нажав левую или правую кнопку мыши, можно получить значение функции, соответствующее выбранной линии. Для того, чтобы завершить оцифровку линий уровня, перекрестье следует поместить за пределы графика и нажать любую кнопку мыши.

На рис. 5.26 представлен результат оцифровки с помощью команды clabel(C,H,’manual’)четырех линий уровня, рассчитанных применительно к условиям примера 19.

Рис. 5.26

MATLABпозволяет строить линии уровня не только на плоскости, но и на графике двухмерной функции z(x,y). Для этого применяется команда surfc(x,y,z), правила использования которого аналогичны правилам для команды surf(x,y,z).

Если в примере 17 для вывода графика сделать замену команды mesh(x,y,z)на команду surfc(x,y,z), то получим результат, показанный на рис. 5.27.

Рис. 5.27

Не нашли, что искали? Воспользуйтесь поиском по сайту: