Метод штрафных функций решения задачи нелинейного программирования. Задача нелинейного программирования сформулирована выше. Изменим лишь форму записи ограничений с (33) на следующую
 (38) (38)
Основная идея метода штрафной функции состоит в преобразовании задачи минимизации функции

с соответствующими ограничениями, наложенными на  , в задачу поиска минимума без ограничений функции , в задачу поиска минимума без ограничений функции
 . .
Функция  является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию  , т.е. увеличивала ее значение. В этом случае минимум , т.е. увеличивала ее значение. В этом случае минимум  будет находится внутри области ограничений. Функция будет находится внутри области ограничений. Функция  , удовлетворяющая этому условию, может быть не единственной. , удовлетворяющая этому условию, может быть не единственной.
Функцию  удобно записать следующим образом удобно записать следующим образом
 , ,
где  – положительная величина. Тогда функция – положительная величина. Тогда функция  принимает вид принимает вид
 (39) (39)
Если  принимает допустимые значения, т.е. значения, для которых принимает допустимые значения, т.е. значения, для которых  , то , то  принимает значения, которые больше соответствующих значений принимает значения, которые больше соответствующих значений  (истинной целевой функцией данной задачи), и разность можно уменьшить за счет тог, что (истинной целевой функцией данной задачи), и разность можно уменьшить за счет тог, что  может быть очень малой величиной. Но если может быть очень малой величиной. Но если  принимает значения, которые хотя и являются допустимыми, но близки к границе области ограничений, и, по крайней мере, одна из функций принимает значения, которые хотя и являются допустимыми, но близки к границе области ограничений, и, по крайней мере, одна из функций  близка к нулю, тогда значения функции близка к нулю, тогда значения функции  и, следовательно, значения функции и, следовательно, значения функции  станут очень велики. Таким образом, влияние функции станут очень велики. Таким образом, влияние функции  состоит в создании «гребня с крутыми краями» вдоль каждой границы области ограничений. Следовательно, если поиск начинается из допустимой точки и осуществляется поиск минимума функции состоит в создании «гребня с крутыми краями» вдоль каждой границы области ограничений. Следовательно, если поиск начинается из допустимой точки и осуществляется поиск минимума функции  без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая  достаточно малой величиной, для того чтобы влияние достаточно малой величиной, для того чтобы влияние  было малым в точке минимума, можно сделать точку минимума функции было малым в точке минимума, можно сделать точку минимума функции  без ограничений совпадающей с точкой минимума функции без ограничений совпадающей с точкой минимума функции  с ограничениями. с ограничениями.
Рассмотрим пример, позволяющий понять суть метода.
Пример 2. Требуется минимизировать функцию  при ограничениях при ограничениях 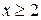 . Минимальным значением функции является . Минимальным значением функции является  . .
Функция  будет следующей: будет следующей:
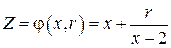 . .
На рис. 10. изображен график функции  и показано положение точек ее минимума для различных значений и показано положение точек ее минимума для различных значений  (1; 0.25; 0.01). (1; 0.25; 0.01).
Область ограничений лежит справа от вертикальной прямой  . Нетрудно видеть, что последовательность точек . Нетрудно видеть, что последовательность точек  стремиться к точке стремиться к точке  – минимуму функции при наличии ограничений. Действительно, найдем минимум функции – минимуму функции при наличии ограничений. Действительно, найдем минимум функции  , решая уравнение , решая уравнение

Приравнивая производную нулю, получаем

то есть

Проверяем достаточное условие
 . .
Минимум достигается при  внутри области ограничений. Следовательно функция внутри области ограничений. Следовательно функция  имеет минимум, равный имеет минимум, равный  при при  . Тогда . Тогда 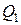 есть точка с координатами (3; 4), есть точка с координатами (3; 4),  –с координатами (2.5; 3), –с координатами (2.5; 3),  –с координатами (2.1; 2.2). Ясно, что при –с координатами (2.1; 2.2). Ясно, что при  минимум без ограничений функции минимум без ограничений функции  приближается к значению 2 и минимальной точкой является точка приближается к значению 2 и минимальной точкой является точка  . В общем случае невозможно аналитически определить положение минимума функции . В общем случае невозможно аналитически определить положение минимума функции  , рассматривая ее как обычную функцию от , рассматривая ее как обычную функцию от  . Обычно используются численные методы. . Обычно используются численные методы.
Обобщим результаты, полученные в примере 2., на общий случай задачи нелинейного программирования.
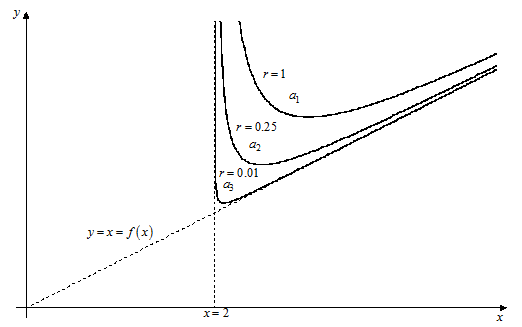
Рис. 10. Иллюстрация к примеру 2.
Предположим, что  – минимальные точки функции – минимальные точки функции  для убывающей последовательности значений для убывающей последовательности значений  , стремящейся к нулю. Тогда последовательность точек , стремящейся к нулю. Тогда последовательность точек  сходится к оптимальному решению задачи с ограничениями (32), (38) при сходится к оптимальному решению задачи с ограничениями (32), (38) при 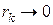 . .
Следовательно,

и
 , ,
где  – минимальная точка функции – минимальная точка функции  при наличии ограничений. при наличии ограничений.
Полученный результат можно доказать следующим образом. Поскольку  непрерывная функция и непрерывная функция и 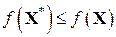 для всех допустимых точек, то задав произвольное достаточно малое значение для всех допустимых точек, то задав произвольное достаточно малое значение  , можно найти допустимую точку , можно найти допустимую точку  , такую, что , такую, что
 . (40) . (40)
Поскольку 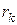 – убывающая последовательность, стремящаяся к нулю, можно найти такое значение – убывающая последовательность, стремящаяся к нулю, можно найти такое значение  , что для , что для  справедливо неравенство справедливо неравенство
 (41) (41)
Поскольку  из определения функции из определения функции  , имеем , имеем

где  – минимальная точка функции – минимальная точка функции  для задачи без ограничений. для задачи без ограничений.
Кроме того, если  , то , то  и справедливо неравенство и справедливо неравенство
 . .
Это следует из того, что поскольку  минимизирует функцию минимизирует функцию  и в любой другой точке области и в любой другой точке области  , в частности в точке , в частности в точке  , функция будет принимать значение, большее чем , функция будет принимать значение, большее чем  . Поэтому . Поэтому
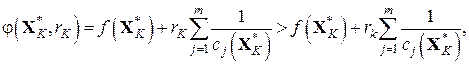
поскольку  . Следовательно, . Следовательно,
 . .
Тогда
 . (42) . (42)
Но так как значение  минимизирует функцию минимизирует функцию  , то , то
 . (43) . (43)
Следовательно, из условий (42) и (43) получим
 . .
Из выражения (41) следует, что
 . .
Тогда из (40) следует, что
 , ,
и
 . .
Поскольку  может быть выбрано произвольно малым, всегда можно найти такое значение может быть выбрано произвольно малым, всегда можно найти такое значение  , при котором , при котором
 . .
Таким образом, при  

Из приведенного выше доказательства следует, что при 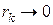
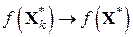 и и  . .
Последовательность  образует убывающую последовательность, такую, что образует убывающую последовательность, такую, что
 . .
Для обеспечения сходимости метода, основанного на штрафовых функциях необходимо, чтобы последовательность констант 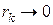 . Поэтому можно предложить следующий алгоритм решения задачи. . Поэтому можно предложить следующий алгоритм решения задачи.
Для заданной минимизируемой функции  и ограничений и ограничений  выбирается начальное значение выбирается начальное значение  , формируется функция , формируется функция  , которая минимизируется c использованием любого метода, предназначенного для безусловной минимизации, например, метода ДФП. Определив минимум , которая минимизируется c использованием любого метода, предназначенного для безусловной минимизации, например, метода ДФП. Определив минимум  , необходимо уменьшить значение , необходимо уменьшить значение  . Например положить . Например положить  (константа (константа  ). Затем минимизировать новую функцию ). Затем минимизировать новую функцию 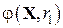 , вновь используя метод безусловной минимизации. Таким образом реализуется итерационная процедура. На , вновь используя метод безусловной минимизации. Таким образом реализуется итерационная процедура. На  -м шаге минимизируется функция -м шаге минимизируется функция  , минимум которой находится в точке , минимум которой находится в точке  . В качестве исходной точки при безусловной минимизации на . В качестве исходной точки при безусловной минимизации на  -м шаге используется значение полученное на предыдущем шаге. Параметр -м шаге используется значение полученное на предыдущем шаге. Параметр  меняется в ходе итерационного процесса в соответствии с зависимостью меняется в ходе итерационного процесса в соответствии с зависимостью  . Так как последовательность . Так как последовательность 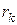 убывает и стремиться к нулю, то последовательность точек минимумов функции убывает и стремиться к нулю, то последовательность точек минимумов функции  сходится к решению задачи с ограничениями. сходится к решению задачи с ограничениями.
Дополнительная литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория базовых знаний. 2001.
2. А.В. Аттетков, С.В. Галкин, В.С. Зарубин Методы оптимизации. М.: МГТУ, 2001, 440 с.
3. В.М. Вержбицкий Численные методы. М.: Высшая школа. 2000, 266 с.
4. В.М. Вержбицкий Основы численных методов. М.: Высшая школа. 2002, 840 с.
5. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир. 1977.
6. Моисеев Н.Н., Иванилов Ю.П., Столяров Е.М. Методы оптимизации. – М.: Наука. 1979.
7. Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука. 1981.
8. Сухарев А.Г., Тимохов А.Ф., Федоров В.В. Курс методов оптимизации. – М.: Наука. 1986.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 (38)
(38)
 , в задачу поиска минимума без ограничений функции
, в задачу поиска минимума без ограничений функции .
. является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию
является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию  , т.е. увеличивала ее значение. В этом случае минимум
, т.е. увеличивала ее значение. В этом случае минимум  ,
, – положительная величина. Тогда функция
– положительная величина. Тогда функция  принимает вид
принимает вид (39)
(39) принимает допустимые значения, т.е. значения, для которых
принимает допустимые значения, т.е. значения, для которых  , то
, то  (истинной целевой функцией данной задачи), и разность можно уменьшить за счет тог, что
(истинной целевой функцией данной задачи), и разность можно уменьшить за счет тог, что  близка к нулю, тогда значения функции
близка к нулю, тогда значения функции  без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая
без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая  при ограничениях
при ограничениях 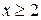 . Минимальным значением функции является
. Минимальным значением функции является  .
.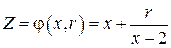 .
. и показано положение точек ее минимума для различных значений
и показано положение точек ее минимума для различных значений  стремиться к точке
стремиться к точке  – минимуму функции при наличии ограничений. Действительно, найдем минимум функции
– минимуму функции при наличии ограничений. Действительно, найдем минимум функции 


 .
. внутри области ограничений. Следовательно функция
внутри области ограничений. Следовательно функция  при
при 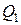 есть точка с координатами (3; 4),
есть точка с координатами (3; 4),  –с координатами (2.5; 3),
–с координатами (2.5; 3),  –с координатами (2.1; 2.2). Ясно, что при
–с координатами (2.1; 2.2). Ясно, что при  минимум без ограничений функции
минимум без ограничений функции 
 – минимальные точки функции
– минимальные точки функции  , стремящейся к нулю. Тогда последовательность точек
, стремящейся к нулю. Тогда последовательность точек  сходится к оптимальному решению задачи с ограничениями (32), (38) при
сходится к оптимальному решению задачи с ограничениями (32), (38) при 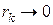 .
.
 ,
, – минимальная точка функции
– минимальная точка функции 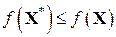 для всех допустимых точек, то задав произвольное достаточно малое значение
для всех допустимых точек, то задав произвольное достаточно малое значение  , можно найти допустимую точку
, можно найти допустимую точку  , такую, что
, такую, что . (40)
. (40)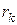 – убывающая последовательность, стремящаяся к нулю, можно найти такое значение
– убывающая последовательность, стремящаяся к нулю, можно найти такое значение  , что для
, что для  справедливо неравенство
справедливо неравенство (41)
(41) из определения функции
из определения функции  , имеем
, имеем
 – минимальная точка функции
– минимальная точка функции  , то
, то  и справедливо неравенство
и справедливо неравенство .
. , функция будет принимать значение, большее чем
, функция будет принимать значение, большее чем  . Поэтому
. Поэтому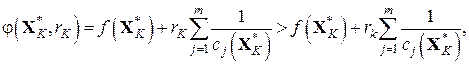
 . Следовательно,
. Следовательно, .
. . (42)
. (42) , то
, то . (43)
. (43) .
. .
. ,
, .
. , при котором
, при котором .
.


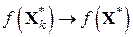 и
и  .
. образует убывающую последовательность, такую, что
образует убывающую последовательность, такую, что .
. выбирается начальное значение
выбирается начальное значение  , формируется функция
, формируется функция  (константа
(константа  ). Затем минимизировать новую функцию
). Затем минимизировать новую функцию 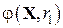 , вновь используя метод безусловной минимизации. Таким образом реализуется итерационная процедура. На
, вновь используя метод безусловной минимизации. Таким образом реализуется итерационная процедура. На  . В качестве исходной точки при безусловной минимизации на
. В качестве исходной точки при безусловной минимизации на  . Так как последовательность
. Так как последовательность