
|
|
Градиентные методы поиска минимума.Метод наискорейшего спуска. Данный метод дает возможность на каждом шаге поиска минимума двигаться вдоль «наилучшего» направления. Известно, что направление градиента является направлением наискорейшего возрастания функции. Следовательно, противоположное направление является направлением наискорейшего убывания функции. Это свойство может быть обосновано следующим образом. Предположим, что осуществляется перемещение из точки
а
Изменение значений функции определяется соотношениями
с точностью до первого порядка Выражение (5) запишем в виде
где
Как видим, формула (6) определяет направление наибольшего возрастания функции Если мы находимся на текущем шаге в точке
или, в скалярной форме
В формуле (7)
Причем оптимальное значение Оканчивать вычислительный процесс можно, сравнивая по норме в каком либо пространстве две соседние точки итерационного процесса (7), т.е.
или определяя норму градиента
Эти формулы можно переписать в виде
где Более эффективными являются методы, использующие информацию о вторых частных производных минимизируемой функции. Если функция
Это свойство можно использовать для поиска минимума. Метод поиска минимума на основе квадратичной аппроксимации. Квадратичная функция
где
откуда Согласно (6.9), функция Разумной аппроксимацией минимума функции
откуда
Если точку
или, с регулируемой скоростью движения к минимуму
Здесь
Оканчивается вычислительный процесс так же, как и в градиентном методе. Скорость сходимости метода достаточно высока, особенно в окрестности экстремальной точки, так как функция Давидон, Флетчер и Пауэлл предложили метод, который позволяет избежать вычисления обратной матрицы Гессе. В основе лежат формулы (9), (10). Метод Давидона – Флетчера – Пауэлла.Суть метода Давидона – Флетчера – Пауэлла (ДФП) состоит в том, что направление поиска на
Рассмотрим алгоритм метода ДФП. Начнем поиск из начальной точки 1. На шаге 2. В качестве направления поиска выбираем направление 3. Находим значение 4. Находим приращение (приближение) к точке экстремума
5. Определяем следующую аппроксимацию точки экстремума, то есть реализуем итерационный процесс
6. Вычисляем 7. Полагаем
8. Вычисляем матрицу
где
9. Вновь выполняем итерационный процесс, вернувшись на шаг 2. Ранее отмечалось, что в процессе итераций на определенном шаге матрица
Заметим, что из выражения (12) следует
Из соотношений (13) – (15) с учетом того, что
Из последнего соотношения и следует (16). Таким образом, векторы
Данный алгоритм эффективно работает при минимизации большинства функций вне зависимости от того, квадратичны они в окрестности точки экстремума или нет. На рис. 9. приведена укрупненная структурная схема алгоритма метода ДФП.
Рис. 9. Укрупненная структурная схема алгоритма минимизации функции n переменных методом ДФП
Отметим, что очень близким по концепции является метод Флетчера – Ривса. В основе лежит итерационная процедура, определенная формулой (9).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 в следующую точку
в следующую точку  , где
, где  – некоторое направление, а
– некоторое направление, а  – шаг некоторой длины. Следовательно, перемещение производится из точки
– шаг некоторой длины. Следовательно, перемещение производится из точки  в точку
в точку 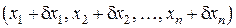 , где
, где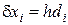 ,
,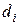 – косинусы направления
– косинусы направления  .
.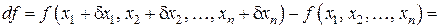
 (5)
(5) , причем частные производные вычисляются в точке
, причем частные производные вычисляются в точке  , (6)
, (6) ,
, .
.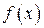 . Поэтому направлением наискорейшего спуска является направление
. Поэтому направлением наискорейшего спуска является направление  .
. , то следующей точкой, аппроксимирующей минимум
, то следующей точкой, аппроксимирующей минимум  , которая оценивается по формуле
, которая оценивается по формуле (7)
(7) .
. – значение шага, определяющего скорость движения по направлению к минимуму. Оптимальное значение шага
– значение шага, определяющего скорость движения по направлению к минимуму. Оптимальное значение шага 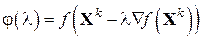 .
. можно найти, используя любой метод минимизации функции одного переменного.
можно найти, используя любой метод минимизации функции одного переменного. ,
, .
. ,
, ,
, ,
,  –заданные положительные значения точности вычислений. Недостаток метода – низкая скорость сходимости, прежде всего в малой окрестности точки минимума.
–заданные положительные значения точности вычислений. Недостаток метода – низкая скорость сходимости, прежде всего в малой окрестности точки минимума. . Если ограничиться в ряде Тейлора первыми тремя членами, то она аппроксимируется квадратичной функцией
. Если ограничиться в ряде Тейлора первыми тремя членами, то она аппроксимируется квадратичной функцией (8)
(8) ,
, ,
,  – постоянный вектор и
– постоянный вектор и  – имеет минимум в точке
– имеет минимум в точке  , причем
, причем  .
. .
. аппроксимируется квадратичной функцией
аппроксимируется квадратичной функцией  .
.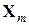 ,то
,то ,
, .
. взять за исходную на
взять за исходную на  -м шаге итерационного процесса, то последующую можно найти по формуле
-м шаге итерационного процесса, то последующую можно найти по формуле , (9)
, (9) . (10)
. (10) – длина шага, определяемая при минимизации функции
– длина шага, определяемая при минимизации функции .
. , а направлением
, а направлением  , где
, где  – симметричная матрица, которая обновляется на каждом шаге и в пределе становится равной обратному гессиану. То есть реализуется следующий алгоритм
– симметричная матрица, которая обновляется на каждом шаге и в пределе становится равной обратному гессиану. То есть реализуется следующий алгоритм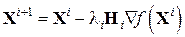 . (11)
. (11) (обычную единичную матрицу, хотя в этом случае может подойти любая симметрическая положительно определенная матрица). Итерационная процедура может быть представлена следующим образом (вместо
(обычную единичную матрицу, хотя в этом случае может подойти любая симметрическая положительно определенная матрица). Итерационная процедура может быть представлена следующим образом (вместо  удобнее писать
удобнее писать  ).
). и положительно определенная симметрическая матрица
и положительно определенная симметрическая матрица  .
. , используя методы минимизации функции одной переменной.
, используя методы минимизации функции одной переменной. .
.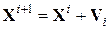 .
. и
и 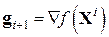 . Проверяем выпонение условия
. Проверяем выпонение условия 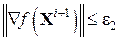 или
или  . Замечание: в полагаемой точке экстремума
. Замечание: в полагаемой точке экстремума  .
. . (12)
. (12) для следующей итерации
для следующей итерации , (13)
, (13) , (14)
, (14)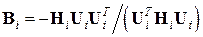 . (15)
. (15) . Если это произойдет за
. Если это произойдет за  шагов, то поиск минимума функции
шагов, то поиск минимума функции 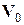 ,
,  , …,
, …,  – линейно независимые векторы матрицы
– линейно независимые векторы матрицы  с собственными значениями, равными единице, то есть
с собственными значениями, равными единице, то есть . (16)
. (16) .
. и
и  можно сократить, следует
можно сократить, следует .
. с собственными значениями, равными единице. Таким образом,
с собственными значениями, равными единице. Таким образом, .
.