Методы поиска минимума для функции многих переменных
Методы поиска минимума для функции одной переменной
Все численные методы можно разделить на две группы: прямые, в которых для поиска минимума используются только значения самой функции, и градиентные, в которых используется значение производной функции 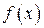 . Последние также используются для поиска минимума функции многих переменных. . Последние также используются для поиска минимума функции многих переменных.
Рассмотрим идею, лежащую в основе прямых методов. Предположим, что точки  и и  определяют (возможно, очень грубо) интервал, который содержит истинную точку минимума, и внутри этого интервала функция унимодальная, то есть имеет один минимум в точке определяют (возможно, очень грубо) интервал, который содержит истинную точку минимума, и внутри этого интервала функция унимодальная, то есть имеет один минимум в точке 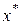 . Следовательно, данная функция имеет форму, близкую к той, что приведена на рис. 1. Если известны значения функции такого вида в трех точках . Следовательно, данная функция имеет форму, близкую к той, что приведена на рис. 1. Если известны значения функции такого вида в трех точках  , ,  , ,  , таких, что , таких, что  , а , а  и и  , то , то  . .
Тогда точка 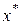 будет лежать внутри интервала будет лежать внутри интервала  , меньшего по размеру, чем интервал , меньшего по размеру, чем интервал  . .
Последовательно уменьшая интервал неопределенности, можно определить с заданной точностью точку, в которой достигается минимум функции 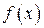 . .

Рис. 1. График унимодальной функции
Естественно задаться вопросом: как определить минимум функции, выполняя минимальное количество вычислений ее значения в промежуточных точках? Как следует выбрать эти точки?
Поиск минимума методом Фибоначчи. Очевидно, что не следует искать решение для всех точек, получаемых в результате эксперимента. Надо попытаться сделать так, чтобы значения функции, полученные в предыдущих экспериментах, определяли положение последующих точек. Действительно, зная значения функции, мы тем самым имеем информацию о самой функции и положении ее минимума и используем эту информацию в дальнейшем поиске.
Предположим, что имеется интервал неопределенности  и известно значение функции и известно значение функции  внутри этого интервала (см. рис. 1.). Если можно вычислить функцию всего один раз в точке внутри этого интервала (см. рис. 1.). Если можно вычислить функцию всего один раз в точке  , то где следует поместить точку , то где следует поместить точку  , для того чтобы получить наименьший возможный интервал неопределенности? , для того чтобы получить наименьший возможный интервал неопределенности?
Положим  и и  , причем , причем  , как показано на рис. 1., и эти значения будут фиксированы, если известны , как показано на рис. 1., и эти значения будут фиксированы, если известны  , ,  и и  . Если . Если  находится в интервале находится в интервале  , то: , то:
1. если 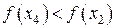 , то новым интервалом неопределенности будет , то новым интервалом неопределенности будет  длиной длиной  ; ;
2. если 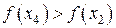 , то новым интервалом неопределенности будет , то новым интервалом неопределенности будет  длиной длиной  . .
Поскольку не известно, какая из этих ситуаций будет иметь место, выберем  таким образом, чтобы минимизировать наибольшую из длин таким образом, чтобы минимизировать наибольшую из длин  и и 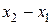 . Достигнуть этого можно, сделав длины . Достигнуть этого можно, сделав длины  и и 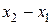 равными, то есть поместив равными, то есть поместив  внутри интервала симметрично относительно точки внутри интервала симметрично относительно точки  , уже лежащей внутри интервала. Любое другое положение точки , уже лежащей внутри интервала. Любое другое положение точки  может привести к тому, что полученный интервал будет больше может привести к тому, что полученный интервал будет больше  . .
Помещаем  симметрично относительно точки симметрично относительно точки  . .
Если окажется, что можно выполнить еще одно вычисление функции, то следует применить описанную процедуру к интервалу  , в котором уже есть значение функции, вычисленное в точке , в котором уже есть значение функции, вычисленное в точке  , или к интервалу , или к интервалу  , в котором уже есть значение функции, вычисленное в точке , в котором уже есть значение функции, вычисленное в точке  . Следовательно, нужно поместить следующую точку внутри интервала неопределенности симметрично относительно уже находящейся там точки. . Следовательно, нужно поместить следующую точку внутри интервала неопределенности симметрично относительно уже находящейся там точки.
Рассмотрим, каким образом организуется процесс вычислений. Начнем с предполагаемого окончания вычислительного процесса.
На  -м вычислении -м вычислении  -ю точку следует поместить симметрично по отношению к -ю точку следует поместить симметрично по отношению к  -й точке. Положение этой последней точки зависит от экспериментатора. Для того, чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка -й точке. Положение этой последней точки зависит от экспериментатора. Для того, чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка  будет совпадать с точкой будет совпадать с точкой  . Однако при этом не получается никакой новой информации. Обычно точки . Однако при этом не получается никакой новой информации. Обычно точки  и и  отстоят друг от друга на достаточном расстоянии, чтобы определить, в какой половине, левой или правой, находится интервал неопределенности. Они помещаются на расстоянии отстоят друг от друга на достаточном расстоянии, чтобы определить, в какой половине, левой или правой, находится интервал неопределенности. Они помещаются на расстоянии  по обе стороны от середины отрезка по обе стороны от середины отрезка 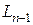 ; можно произвольно задать величину ; можно произвольно задать величину  или выбрать эту величину равной минимально возможному расстоянию между двумя точками. или выбрать эту величину равной минимально возможному расстоянию между двумя точками.
Интервал неопределенности будет иметь длину  , следовательно, , следовательно,
 (рис. 2., нижняя часть). (рис. 2., нижняя часть).
На предыдущем этапе точки  и и  должны быть помещены симметрично внутри интервала должны быть помещены симметрично внутри интервала  на расстоянии на расстоянии 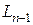 от концов этого интервала. Следовательно, от концов этого интервала. Следовательно,
 (рис. 2., средняя часть). (рис. 2., средняя часть).

Рис. 2. Схема организации эксперимента на последней, предыдущей и пре предыдущей итерациях
Из рисунка видно, что на предпоследнем этапе  остается в качестве внутренней точки. остается в качестве внутренней точки.
Аналогично
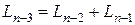 (рис. 2. верхняя часть) (рис. 2. верхняя часть)
В общем случае
 при при  (1.) (1.)
Таким образом,
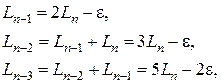
 , ,
и т.д.
Если определить последовательность чисел Фибоначчи следующим образом:  и и  для для  , то , то

Если начальный интервал 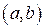 имеет длину имеет длину  , то , то
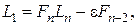
то есть
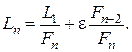
Следовательно, произведя  вычислений функции, можно уменьшить начальный интервал неопределенности в вычислений функции, можно уменьшить начальный интервал неопределенности в  раз по сравнению с его начальной длиной (пренебрегая раз по сравнению с его начальной длиной (пренебрегая  ), и это – наилучший результат. ), и это – наилучший результат.
Если поиск начат, то его несложно продолжить, используя описанное выше правило симметрии. Следовательно, необходимо найти положение первой точки, которая помещена на расстоянии  от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии  от конца интервала: от конца интервала:
 (2.) (2.)
После того, как найдено положение первой точки, числа Фибоначчи больше не нужны. Используемое значение  может определяться из практических соображений. Оно должно быть меньше может определяться из практических соображений. Оно должно быть меньше 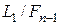 , иначе будут иметь место лишние вычисления значений функции , иначе будут иметь место лишние вычисления значений функции  . .
Таким образом, поиск методом Фибоначчи, названный так ввиду появления при поиске чисел Фибоначчи, является итерационной процедурой. В процессе поиска интервала  с точкой с точкой  , уже лежащей в этом интервале, следующая точка , уже лежащей в этом интервале, следующая точка  всегда выбирается такой, что всегда выбирается такой, что  или или 
Обозначим  и и  , тогда можно рассмотреть четыре случая организации вычислительного процесса: , тогда можно рассмотреть четыре случая организации вычислительного процесса:
1.  : новый интервал : новый интервал  , содержащий точку , содержащий точку  (рис. 3.а) (рис. 3.а)
2.  : новый интервал : новый интервал  , содержащий точку , содержащий точку  (рис. 3.б) (рис. 3.б)
3.  : новый интервал : новый интервал  , содержащий точку , содержащий точку  (рис. 3.в) (рис. 3.в)
4.  : новый интервал : новый интервал  , содержащий точку , содержащий точку  (рис. 3.г) (рис. 3.г)
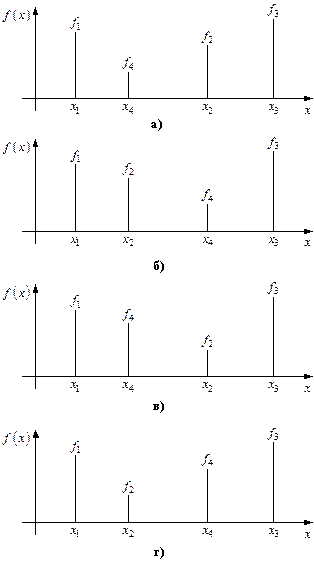
Рис. 3. Схема организации вычислений по методу Фибоначчи
Оканчивать вычислительный процесс можно двумя способами. Либо выполнить намеченные ранее  вычислений, либо, если в процессе вычислений интервал неопределенности станет меньше заданной величины. вычислений, либо, если в процессе вычислений интервал неопределенности станет меньше заданной величины.
2. Поиск методом золотого сечения. Не всегда можно заранее определить, сколько раз придется вычислять функцию. В методе Фибоначчи это нужно знать для определения  , то есть положения начальной точки (см. уравнение (2.)). , то есть положения начальной точки (см. уравнение (2.)).
Метод золотого сечения почти столь же эффективен, как и метод Фибоначчи, однако при этом не требует знать  – количество вычислений функции, определяемое вначале. После того как выполнено – количество вычислений функции, определяемое вначале. После того как выполнено  вычислений, исходя из тех же соображений, что и ранее (см. выражение (1.)), записываем вычислений, исходя из тех же соображений, что и ранее (см. выражение (1.)), записываем
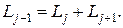
Однако, если  неизвестно, то мы не можем использовать условие неизвестно, то мы не можем использовать условие  . Если отношение последующих интервалов будет постоянным, т.е. . Если отношение последующих интервалов будет постоянным, т.е.
(3.)
то 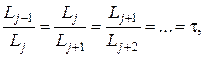

то есть 
Таким образом, 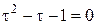 , откуда , откуда  . Тогда . Тогда

и так далее.
Следовательно,  то есть то есть

В результате анализа двух рассмотренных значений функции будет определен интервал, который должен исследоваться в дальнейшем. Это интервал будет содержать одну из предыдущих точек и следующую точку, помещаемую симметрично ей. Первая точка находится на расстоянии  от одного конца интервала, вторая – на таком же расстоянии от другого. Поскольку от одного конца интервала, вторая – на таком же расстоянии от другого. Поскольку 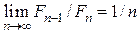 , то из уравнения (2) видно, что поиск методом золотого сечения является предельной формой поиска методом Фибоначчи. Название «золотое сечение» произошло от названия отношения в уравнении (3.). Видно, что , то из уравнения (2) видно, что поиск методом золотого сечения является предельной формой поиска методом Фибоначчи. Название «золотое сечение» произошло от названия отношения в уравнении (3.). Видно, что  делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому золотому отношению. делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому золотому отношению.
Таким образом, если определяется интервал  и имеется два значения функции и имеется два значения функции  и и  в точках в точках  и и  , то имеет место два случая (рис. 4.): , то имеет место два случая (рис. 4.):
1.  . Новый интервал неопределенности . Новый интервал неопределенности  (рис. 4. а). (рис. 4. а).
2.  . Новый интервал неопределенности . Новый интервал неопределенности  (рис. 4. б). (рис. 4. б).

Рис. 4. Схема принятия решения в интервале золотого сечения
Оканчивать вычислительный процесс можно также как и в методе Фибоначчи.
3. Метод поиска минимума функции, основанный на ее аппроксимации полиномом второй степени. Рассмотренный ниже подход к поиску минимума функции 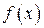 также может быть использован при ее аппроксимации полиномами более высокого порядка. Очевидным является, что получаемая в этих случаях точность будет выше. также может быть использован при ее аппроксимации полиномами более высокого порядка. Очевидным является, что получаемая в этих случаях точность будет выше.
Рассмотрим основную идею и ее реализацию в виде конкретного алгоритма при аппроксимации функции 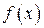 квадратичным полиномом. квадратичным полиномом.
Если известны значения функции 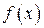 в трех различных точках в трех различных точках 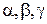 , равные соответственно , равные соответственно  , то функция , то функция 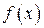 может быть аппроксимирована квадратичной функцией может быть аппроксимирована квадратичной функцией
 , ,
где A, B и C определяются из уравнений

После преобразований этих уравнений получаем

где  . Ясно, что . Ясно, что  будет иметь минимум в точке будет иметь минимум в точке  , если , если  . Следовательно, можно аппроксимировать точку минимума функции . Следовательно, можно аппроксимировать точку минимума функции 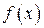 значением значением
 . (4) . (4)
Алгоритм поиска минимума в данном случае может быть следующим.
Пусть задана унимодальная функция 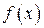 , начальная аппроксимация положения минимума и длина шага , начальная аппроксимация положения минимума и длина шага  , являющаяся величиной того же порядка, что и расстояние из точки А до точки истинного минимума , являющаяся величиной того же порядка, что и расстояние из точки А до точки истинного минимума 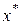 (условие, которое не всегда просто удовлетворить). Вычислительная процедура имеет следующие шаги: (условие, которое не всегда просто удовлетворить). Вычислительная процедура имеет следующие шаги:
1. Вычислить  и и  . .
2. Если  , то взять в качестве третьей точки , то взять в качестве третьей точки  и вычислить и вычислить  . В противном случае, в качестве третьей точки взять . В противном случае, в качестве третьей точки взять  и найти и найти  (рис. 5.) (рис. 5.)
3. Используя эти точки, найти  из уравнения (4.) и вычислить из уравнения (4.) и вычислить  . .
4. Если разница между полученным наименьшим значением функции и предыдущим наименьшим значением функции меньше заданной точности, то процедура заканчивается.
5. Если процедура не завершалась на шаге 4, то точка с наибольшим значением обычно отбрасывается, и возвращается на шаг 3. Но если, оставив точку с наибольшим значением функции, мы определим конечные границы интервала, в котором лежит минимум, то следует действительно оставить это значение и затем вернуться на шаг 3.
Рис.5. Схема принятия решения при квадратичной аппроксимации минимизации функции
Методы поиска минимума для функции многих переменных
Численные методы поиска минимума функции n переменных также делятся на две группы: методы прямого поиска, то есть те, где используются только значения функций и градиентные методы – использующие значения производных функции.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


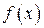 . Последние также используются для поиска минимума функции многих переменных.
. Последние также используются для поиска минимума функции многих переменных. и
и  определяют (возможно, очень грубо) интервал, который содержит истинную точку минимума, и внутри этого интервала функция унимодальная, то есть имеет один минимум в точке
определяют (возможно, очень грубо) интервал, который содержит истинную точку минимума, и внутри этого интервала функция унимодальная, то есть имеет один минимум в точке 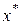 . Следовательно, данная функция имеет форму, близкую к той, что приведена на рис. 1. Если известны значения функции такого вида в трех точках
. Следовательно, данная функция имеет форму, близкую к той, что приведена на рис. 1. Если известны значения функции такого вида в трех точках  ,
,  ,
,  , таких, что
, таких, что  , а
, а  и
и  , то
, то  .
. , меньшего по размеру, чем интервал
, меньшего по размеру, чем интервал  .
.
 внутри этого интервала (см. рис. 1.). Если можно вычислить функцию всего один раз в точке
внутри этого интервала (см. рис. 1.). Если можно вычислить функцию всего один раз в точке  , то где следует поместить точку
, то где следует поместить точку  и
и  , причем
, причем  , как показано на рис. 1., и эти значения будут фиксированы, если известны
, как показано на рис. 1., и эти значения будут фиксированы, если известны  , то:
, то: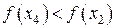 , то новым интервалом неопределенности будет
, то новым интервалом неопределенности будет 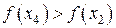 , то новым интервалом неопределенности будет
, то новым интервалом неопределенности будет  длиной
длиной  .
.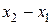 . Достигнуть этого можно, сделав длины
. Достигнуть этого можно, сделав длины  .
. -м вычислении
-м вычислении  -й точке. Положение этой последней точки зависит от экспериментатора. Для того, чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка
-й точке. Положение этой последней точки зависит от экспериментатора. Для того, чтобы получить наибольшее уменьшение интервала на данном этапе, следует разделить пополам предыдущий интервал. Тогда точка  будет совпадать с точкой
будет совпадать с точкой  . Однако при этом не получается никакой новой информации. Обычно точки
. Однако при этом не получается никакой новой информации. Обычно точки  по обе стороны от середины отрезка
по обе стороны от середины отрезка 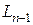 ; можно произвольно задать величину
; можно произвольно задать величину  или выбрать эту величину равной минимально возможному расстоянию между двумя точками.
или выбрать эту величину равной минимально возможному расстоянию между двумя точками. , следовательно,
, следовательно, (рис. 2., нижняя часть).
(рис. 2., нижняя часть). должны быть помещены симметрично внутри интервала
должны быть помещены симметрично внутри интервала  на расстоянии
на расстоянии  (рис. 2., средняя часть).
(рис. 2., средняя часть).
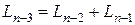 (рис. 2. верхняя часть)
(рис. 2. верхняя часть) при
при  (1.)
(1.)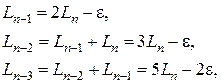
 ,
, и
и  для
для  , то
, то
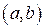 имеет длину
имеет длину  , то
, то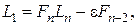
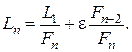
 раз по сравнению с его начальной длиной (пренебрегая
раз по сравнению с его начальной длиной (пренебрегая  от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии
от одного из концов начального интервала, причем не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии  (2.)
(2.)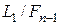 , иначе будут иметь место лишние вычисления значений функции
, иначе будут иметь место лишние вычисления значений функции  с точкой
с точкой  или
или 
 и
и  , тогда можно рассмотреть четыре случая организации вычислительного процесса:
, тогда можно рассмотреть четыре случая организации вычислительного процесса: : новый интервал
: новый интервал  : новый интервал
: новый интервал  , содержащий точку
, содержащий точку  : новый интервал
: новый интервал  , содержащий точку
, содержащий точку  : новый интервал
: новый интервал  , содержащий точку
, содержащий точку 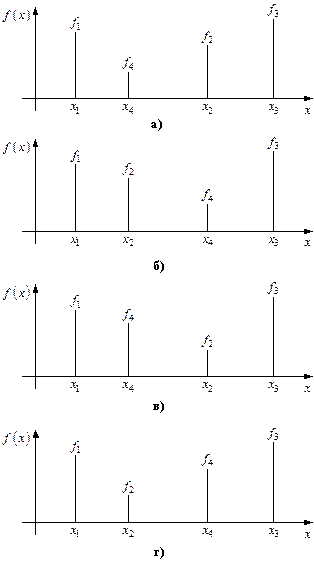
 вычислений, исходя из тех же соображений, что и ранее (см. выражение (1.)), записываем
вычислений, исходя из тех же соображений, что и ранее (см. выражение (1.)), записываем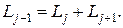
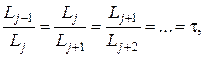


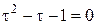 , откуда
, откуда  . Тогда
. Тогда
 то есть
то есть
 от одного конца интервала, вторая – на таком же расстоянии от другого. Поскольку
от одного конца интервала, вторая – на таком же расстоянии от другого. Поскольку 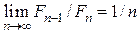 , то из уравнения (2) видно, что поиск методом золотого сечения является предельной формой поиска методом Фибоначчи. Название «золотое сечение» произошло от названия отношения в уравнении (3.). Видно, что
, то из уравнения (2) видно, что поиск методом золотого сечения является предельной формой поиска методом Фибоначчи. Название «золотое сечение» произошло от названия отношения в уравнении (3.). Видно, что  делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому золотому отношению.
делится на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому золотому отношению. и имеется два значения функции
и имеется два значения функции  и
и  в точках
в точках  . Новый интервал неопределенности
. Новый интервал неопределенности  (рис. 4. а).
(рис. 4. а). . Новый интервал неопределенности
. Новый интервал неопределенности  (рис. 4. б).
(рис. 4. б).
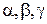 , равные соответственно
, равные соответственно  , то функция
, то функция  ,
,

 . Ясно, что
. Ясно, что  будет иметь минимум в точке
будет иметь минимум в точке  , если
, если  . Следовательно, можно аппроксимировать точку минимума функции
. Следовательно, можно аппроксимировать точку минимума функции  . (4)
. (4) , являющаяся величиной того же порядка, что и расстояние из точки А до точки истинного минимума
, являющаяся величиной того же порядка, что и расстояние из точки А до точки истинного минимума  и
и  .
. , то взять в качестве третьей точки
, то взять в качестве третьей точки  и вычислить
и вычислить  . В противном случае, в качестве третьей точки взять
. В противном случае, в качестве третьей точки взять  и найти
и найти  (рис. 5.)
(рис. 5.) из уравнения (4.) и вычислить
из уравнения (4.) и вычислить  .
.