Арифметические вычисления

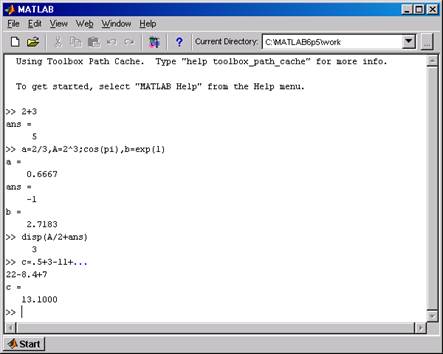
Работа в среде MATLAB может осуществляться либо в программном режиме (см. Главу 4), либо в командном режиме (режиме калькулятора, диалоговом режиме) по правилу «задал вопрос, получил ответ». Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькулятора вычисления, но и операции с векторами и матрицами, комплексными числами, рядами и полиномами. Можно почти мгновенно задать и вывести графики различных функций: от простой синусоиды до сложной трехмерной фигуры.

Основным элементом командного режима работы с системой является главное или командное окно Command Window . Оно активизируется командой View => Desktop Layout => Command Window Only основного меню MATLAB. Структура командного окна аналогична структуре Windows - приложений (рис. 1.2).

Рис. 1.2

Строка в текстовом поле командного окна, отмеченная символом приглашения >>с мигающим курсором, называется строкой ввода или командной строкой. Она предназначена для ввода с клавиатуры команд, чисел, имен переменных и знаков операций, составляющих выражение. Для того, чтобы система MATLAB выполнила введенную команду или вычислила заданное выражение, следует нажать клавишу <Enter>(Ввод).

При вводе курсор может находиться в любом месте командной строки. Введенные выражения вычисляются, а результаты вычислений и выполнения команд появляются в одной или нескольких строках командного окна – строках вывода.

В результате многократных вычислений (нажатий клавиши <Enter>) в командном окне автоматически производится вертикальная протяжка (scrolling): строки сдвигаются на одну позицию вверх, а внизу появляется строка ввода с символом приглашения >>. Информация, которая покинула видимую часть окна, не исчезает. В MATLAB ранее введенные строки команд представляют собой «историю» и запоминаются в стеке команд (см. разд. 1.8).

Для просмотра выполненных команд и результатов вычислений, не умещающихся на экране, имеются полосы горизонтальной и вертикальной протяжки. Использование полос протяжки ничем не отличается от других Windows - приложений. Можно также осуществлять протяжку командного окна с помощью клавиш <PageUp>, <PageDown>, <Ctrl+Home>и<Ctrl+End>.

Клавиши <↑> и <↓>, которые в текстовых редакторах служат для перемещения вверх или вниз по экрану, в MATLAB работают иначе. Они используются для возврата в строку ввода ранее выполненных команд с целью их повторного выполнения или редактирования. После первого нажатия клавиши <↑> в строке ввода отобразится последняя введенная команда, при втором нажатии – предпоследняя и т. д. Клавиша <↓> осуществляет прокрутку команд в противоположном направлении.

Иными словами, текстовое поле окна Command Window располагается в двух принципиально разных зонах: зоне просмотра и зоне редактирования. Зона редактирования находится в командной строке, а вся остальная информация видимой части командного окна – в зоне просмотра.

Пока не нажата клавиша <Enter>, вводимое выражение может быть отредактировано или удалено. В зоне просмотра уже ничего нельзя исправить. Если поместить в нее курсор и нажать какую - либо клавишу на клавиатуре, курсор будет автоматически перемещен в строку ввода, расположенную в зоне редактирования. В то же время, с помощью клавиш <←> и <→> можно перемещать курсор в командной строке.

Невозможность редактирования ранее введенной команды простой установкой курсора в нужную строку является одной из особенностей системы MATLAB.

Сеанс работы с системой MATLABназывается сессией. Иными словами, сессия – это все то, что отображается в командном окне в процессе работы с системой. Команды сессии автоматически образуют список, который выводится в окне Command History, а значения переменных сохраняются в окне Workspase (рис. 1.1).

Например, сессия на рис. 1.2 отображает результаты последовательного ввода четырех команд. Обсудим эти результаты и отметим некоторые особенности вычислений в системеMATLAB:

>> 2+3

ans =

Результату выполненной операции не было присвоено имя, поэтому при выводе он был автоматически обозначен символом ans (ansver – ответ). Под этим именем результат вычислений хранится в памяти компьютера и его можно использовать в последующих вычислениях до тех пор, пока в ходе работы не будет получен новый непоименованный результат. Результат вычислений выводится в строках вывода, не содержащих знака приглашения >>;

>> a=2/3,A=2^3;cos(pi),b=exp(1)

a =

0.6667

ans =

-1

b =

2.7183

В одной командной строке можно ввести несколько команд, разделяя их запятыми либо точками с запятой. Система MATLAB выполняет каждую команду, за которой следует запятая, и отображает результаты в отдельных строках. Результат выполнения команды, за которой следует символ <;>, на экран не выводится, но он сохраняется в памяти и может быть использован в последующих вычислениях.

Знаком присваивания является знак =, а не комбинированный знак :=, принятый, например, в языке программирования Pascalили в системе символьной математики Maple.

После ввода этой командной строки вычисляются и сохраняются в памяти значения выражений a=2/3=0,б667, A=2³=8, ans=cosp =-1, b=e¹=e=2,7183 (e – основание натурального логарифма). Значение переменной A, в отличие от a, ans, b, не выводится на экран из-за символа <;>. При вычислении cosp использовалась системная переменная pi – число p. Число e системной переменной не является, и для его вычисления использована встроенная элементарная функция exp(1). Функции записываются строчными буквами, а их аргументы указываются в круглых скобках. Аргумент встроенной тригонометрической функции cos задан в радианах;

>> disp(A/2+ans)

Команда disp (от слова «дисплей») вычисляет выражение 2³/2+cosp и выводит ответ, но не присваивает его переменной ans, как при обычных вычислениях:

>> A/2+ans

ans =

В дальнейшем disp используется для предотвращения вывода лишней строки ans = в наглядных документах;

>> c=.5+3-11+...

22-8.4+7

c =

13.1000

Иногда требуется ввести в окне Command Window команду, которая слишком длинна, чтобы уместиться на одной строке. При приближении к концу строки можно ввести … (три последовательные точки), нажать клавишу <Enter>и продолжить набор команды на следующей строке. При этом вы не увидите на новой строке символа приглашения >>.

Сессия на рис.1.2 содержит только правильные команды и результаты их выполнения. В общем случае сессия является результатом проб и ошибок. Ее текст, наряду с правильными определениями, содержит сообщения и предупреждения об ошибках (см. разд. 1.8), переопределения функций и переменных, использованную справочную информацию команды help (см. приложение.1, рис. П1, рис. П.2). Если сессия сильно «засорена» лишней информацией, диалог пользователя с системой затрудняется.

Команда очистки экрана clc

>> clc

стирает содержание командного окна MATLAB и размещает символ приглашения >> в левом верхнем углу пустого экрана.

Эта команда, однако, оставляет неизменным содержимое окон Command History и Workspase. Поэтому в «чистом» командном окне можно пользоваться значениями переменных, полученных до ввода команды clc.

Если же появится необходимость отредактировать или повторить ранее выполненную команду, то это легко осуществить с помощью окна Command History. Подробнее работа с оконами Command History и Workspase обсуждается в разделах 1.8 и 1.9.

Переменные– это именованные объекты, хранящие какие – либо данные.

Переменные могут быть числовыми, матричными или символьными, что зависит от типа хранящихся в них данных. Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваиваивается переменной, т.е. пользователь не должен заботиться о том, какие значения будет принимать переменная (комплексные, вещественные или целые).

Имя переменной (ее идентификатор) может содержать до 31 символа и не должно совпадать с именами других переменных, функций, команд и системных переменных MATLAB. Имя переменной должно начинаться с буквы, может содержать цифры и символ подчеркивания. Среда MATLAB чувствителена к регистру букв (переменные a и A не идентичны).

В MATLAB существует несколько имен переменных, являющихся зарезервированными. Переменные с такими именами называются системными. Они задаются после загрузки системы и могут использоваться в арифметических выражениях. Системные переменные могут быть переопределены, т. е. при небходимости им можно присвоить другие значения.

Ниже перечислены основные системные переменные MATLAB:

ans – результат вычисления последнего не сохраненного пользователем выражения;

i, j – мнимая единица (), используемая для задания мнимой части комплексных чисел;

Inf (infinity) – обозначение машинной бесконечности;

NaN – сокращение от слов Not-a-Number (не число), принятое для обозначения неопределенного результата (например, 0/0 или Inf/Inf).

pi – число π ( p=3,141592653589793);

eps – погрешность операций над числами с плавающей точкой, т.е интервал между числом 1.0 и следующим ближайшим числом с плавающей точкой равен 2.2204e-16 или 2^-52;

realmin – минимальное по модулю вещественное число (2.2251e-308 или 2^-1022);

realmax – наибольшее по модулю вещественное число (1.7977e+308 или 2¹⁰²³).

Приоритеты арифметических операций системы MATLAB в порядке убывания следующие:

1. Возведение в степень <^>.

2. Умножение <*> и деление (слева направо </>, справа налево <\>).

3. Сложение <+> и вычитание <–>.

Выполнение операций одинакового приоритета происходит в порядке слева направо. Для изменения порядка выполнения арифметических операторов следует использовать круглые скобки. Кроме арифметических операторов, в MATLAB имеются операторы отношения и логические операторы (см. разд. 4.1).

Полный список операторов и справочную информацию по любому из них можно получить в разделе ops справочной системы MATLAB, используя команды helpили doc (см. Приложение 1).

Основу большинства расчетов составляют вычисления значений арифметических выражений. В них в качестве операндов могут выступать константы, переменные или функции. В отличие от большинства алгоритмических языков, в MATLAB допускается использование операндов - массивов (см. разд. 1.6, 1.7, 1.10). В этом случае результатом вычисления выражения также может быть массив.

Выражения, помещенные между двумя апострофами (заключенные в символьные скобки ' '), рассматриваются как строчные и не вычисляются, даже если в них содержатся математические выражения. Чаще всего они применяются для задания параметров функций и их нечисловых значений, вставки текста в графические объекты, а также для описания символьных переменных и выражений. Так, ввод строки '2+3' приводит к результату

>> '2+3'

ans =

2+3

а не 5.

При выводе графиков символы, помещенные между апострофами, определяют цвет линий графика, их тип и тип маркера, которым метятся линии (Глава 5).

Вещественные числа

Число – простейший объект системы MATLAB, представляющий количественные данные. Основным типом данных, с которым производятся вычисления в системе MATLAB, являются десятичные числа. Они приближают с заданной точностью произвольные вещественные (действительные) числа. Десятичные числа, используемые в MATLAB, могут быть целыми и дробными, например: 0, 1, -93, 7.5674, 0.00000047.

Возможно представление чисел в экспоненциальной форме с указанием мантиссы и порядка числа: 3.3333e -4; -75.8e13.

Для отделения порядка числа от мантиссы применяется символ e, т.е. запись 3.3333e -04 соответствует записи 3.3333×10^-4 или 0.00033333.

Ввод чисел возможен в любом удобном для пользователя виде. Например, проще набрать 10e8 или 1.0e9, чем 1 000 000 000, а результат будет тот же самый. Пробел между цифрами и символом e при вводе не допускается, так как это приводит к сообщению об ошибке:

>> 10 e8

??? 10 e8

Error: Missing operator, comma, or semicolon.

В качестве разделителя целой и дробной частей числа используется точка, а не запятая.

При вводе числа с нулевой целой частью ноль может опускаться: .5 равнозначно 0. 5.

Хотя задавать вещественные числа можно в любой из указанных выше форм, на машинном уровне системы MATLAB они представляются в форме с мантиссой и показателем степени. Этот основной тип данных называется double (формат с двойной точностью). Он задается по умолчанию, и даже целые числа представляются системой MATLAB на машинном уровне в той же форме, что и дробные числа.

Под мантиссу и показатель степени (на машинном уровне используется двоичная система записи) отводится 8 байт памяти. В результате для десятичных чисел достигается точность порядка 15 значащих цифр. Они принимают по модулю значения от 2.2250738507201e -308 до 1.797693134862316e+308. Для этих чисел зарезервированы имена realmin и realmax.

Все операции над числами MATLAB выполняет по умолчанию в формате double. Такой формат удовлетворяет подавляющему большинству требований к численным расчетам, но совершенно не подходит для символьных вычислений с произвольной (абсолютной) точностью (Глава 7).

В MATLABтакже существует тип данных single, который снижает требования к памяти в два раза (под мантиссу и показатель степени отводится 4 байта). Но при сложных вычислениях в этом случае возрастает вероятность получить результат с большой погрешностью.

Существуют и целые типы данных: int8, uint8, int16, uint16, int32, uint32, int64, uint64. Под них отводится 8, 16, 32 и 64 байта соответственно.Буква u соответствует беззнаковым типам данных с диапазоном от 0 до некоторого максимального положительного значения.

Для того чтобы переменная получила тип данных, отличный от double, применяется явный квалификатор , совпадающий с названием типа.

Например,

>> x=int32(3.2)

определяет переменную целого типа int32.

Подробную информацию о перечисленных типах данных можно получить с помощью команд doc double, doc single, doc int8, doc uint8.

Не нашли, что искали? Воспользуйтесь поиском по сайту: