
|
|
Умножение и деление десятичных дробей на целое числоУмножение и деление десятичных дробей на целое число тесно связано с умножением и делением целых чисел. Чтобы подвести учащихся к пониманию того, как производится умножение десятичной дроби на целое число, и сделать обобщение в виде правила, необходимо начать с рассмотрения простейших случаев (при этом учитель должен воспользоваться тем, что учащиеся уже имеют понятие о действии умножения), например: 1,2-3=. В этом выражении действие умножения заменяется действием сложения: 1,2-3 = 1,2+1,2+1,2=3,6, 1,2-3=3,6. Внимание учащихся надо обратить на то, что сначала умножается целое число на множитель и это произведение целых отделяется запятой, а затем умножаются десятые доли на множитель. Подобные случаи умножения (без перехода через разряд ни в одном разряде) выполняются устно. Случаи умножения с переходом через разряд выполняются в столбик:
Множители перемножаются как целые числа и в полученном произведении отделяется запятой справа столько цифр, сколько десятичных знаков в первом множителе. Примеры на умножение десятичной дроби на целое число подираются в той же последовательности, что и примеры на умно-1(ение целых чисел. • Наибольшие трудности для учащихся представляют примеры, в Которых в первом множителе один или несколько десятичных раков равны нулю, а также примеры, в которых в произведении ^случается нуль целых.
0,285 « Подобные примеры надо чаще предъявлять учащимся, повторив предварительно правила умножения нуля на целое число и целого числа на нуль. При делении десятичной дроби на целое число также следует соблюдать определенную последовательность: 1.Все разряды делимого делятся на делитель без остатка: 2. Целое или какая-либо из долей делимого не делится нацело на делитель: 4,86:3.
Делим 4 целых на 3. В частном получаем единицу, отделяем ее запятой. В остатке осталась единица. Дробим ее в десятые доли и прибавляем еще 8 десятых. 18 десятых делим на 3, получаем 6 десятых. Далее 6 сотых делим на 3, получаем 2 сотых. Частное равно 1,62. 3. Особые случаи деления, когда в частном полу-
3) 1:8=?
8 ОД25~
Умножение и деление десятичных дробей, так же как и сое ветствующие действия с целыми числами, изучаются параллельн! Каждое действие учащиеся учатся проверять обратным ему дейс] вием. Решаются также примеры, в которых содержатся действия вой и второй ступени со скобками, чтобы поупражнять учащихс в применении правил порядка действий. Кроме того, следует пре ложить и примеры на нахождение неизвестного множимого, неи| вестного делимого. Запись десятичной дроби в виде обыкновенной и наоборот С выражением десятичной дроби в виде обыкновенной учащи ся уже сталкивались неоднократно. Во-первых, образование дес! тичной дроби рассматривалось как частный случай обыкновение дроби, у которой знаменатель — единица с нулями, во-вторыэ десятичную дробь в виде обыкновенной учащиеся выражали пр знакомстве с действиями над десятичными дробями. Запись дес>1 тичной дроби в виде обыкновенной сводится к записи десятично! 3 7 дроби со знаменателем, например: 0,3=тп; 0.0?=7731 Й7Ч ' 1,873=1^ и т. д. Обратное упражнение, т. е. запись обыкновенной дроби в виде десятичной, выполняется так: У обыкновенной дроби -^ знаменатель дроби 5, у десятичной же дроби знаменатель должен выражаться единицей с нулями, т. е. 10, 100, 1000 и т. д. Подбираем такое число, при умножении на которое числа 5 получалось бы 10, 100, 1000, т. е. знаменатель дроби выразился бы единицей с нулями. Если 5 «2, то получится! 10. Чтобы дробь не изменилась, надо и числитель умножить на 2.< 1 1 • 2 2 3 Следовательно, 5'=5Т2":=То':=^'^' Запишем дробь -? в виде деся- Но не всегда этим способом можно (при замене обыкновенной дроби десятичной) выразить знаменатель обыкновенной дроби 1 с несколькими нулями. Возьмем, например, дробь -я-. Попробуем взять знаменатель 10. Он не подходит, так как нельзя в данном случае получить дополнительный множитель: 10 не делится нацело на 3. То же получим, если возьмем знаменатели 100, 1000. Следовательно, дробь -^ нельзя этим способом выразить десятичной дробью. Существует второй способ замены обыкновенной дроби десятичной. Всякую обыкновенную дробь можно рассматривать как з частное от деления числителя на ее знаменатель. Возьмем дробь -^. Ее можно рассматривать как частное от деления 3 на 4. Выполним деление:
Рассуждение: «3 на 4 не делится нацело. В частном пишем нуль целых и ставим после нуля запятую. Раздробляем 3 в десятые доли. 30 десятых делим на 4. В частном пишем 7 десятых. В остатке 2 десятых. Раздробим 2 десятых в сотые доли. Получим 20 сотых. Делим на 4. В частном 5 сотых.
Итого в частном 0,75. Следовательно, -т-=0,75». Проверка. Нужно частное умножить на делитель. В произведении должно получиться число, равное делимому:
0,75-4=3. После рассмотрения еще нескольких примеров учащиеся ны сами сделать вывод о том, как обыкновенную дробь зал десятичной.
«Вернемся к дроби ^-. Мы видели| , 1 дробь т нельзя заменить десятичной п« способом. Попробуем заменить ее десяти вторым способом, т. е. делением числите^ знаменатель. Если будем продолжать д дальше, то увидим, что всегда в остатке о единица, а в частном 3. Деление можно! должить бесконечно. Но обычно его пред -------------------------- ют, делят до первого, второго или тре! знака после запятой, например: 1:3=0,33| В данном случае деление закончили на тысячных долях. ТМ показывают, что деление можно продолжить и дальше. 0,333..74 приближенное, неточное значение дроби т?. Можно предложит! учащимся обратить в десятичные еще ряд обыкновенных дробей 21513 п - 3"' Б"' !)' 7' 7 и т' д' Получаются приближенные десятичные дроом После рассмотрения замены различных обыкновенных дроои1 десятичными учащиеся убеждаются, что одни обыкновении! дроби можно точно выразить десятичными — в этом случае полу» чаются конечныедесятичные дроби -г = 0,2 , другие же можнС заменить только бесконечнымидесятичными дробями | = 0,333.. ^ Совместные действия с обыкновенными и десятичными дробями После изучения обыкновенных и десятичных дробей программой предусмотрены совместные действия над дробями. Перед изучением этой темы следует повторить отдельно все действия над обыкновенными и десятичными дробями, устно и письменно закрепить замену обыкновенной дроби десятичной и наоборот. Все эти виды упражнений должны быть хорошо отработаны, иначе учащиеся при выполнении совместных действий с дробями столкнутся с непреодолимыми трудностями, что вызовет у школьников с нарушением интеллекта чувство беспомощности, негативное отношение к работе. 338 При выполнении совместных действий с десятичными и обыкновенными дробями в школе VIII вида, как показывает опыт, целесообразнее либо все обыкновенные дроби заменять десятичными и выполнять действия только над десятичными дробями, либо наоборот. Сначала решаются задачи и примеры с двумя компонентами. Учитель, объясняя, как выполнить действие, должен обратить внимание учащихся на целесообразность замены дробей десятичными или обыкновенными. Например, в примере 0,45+-я- целесообразно дробь -д- заменить десятичной, так как это сделает вычисления более простыми. Если же 0,45 заменить обыкновенной дробью, то вычисления будут более громоздкими. В этом учащихся следует убедить, предложив выполнить действия сначала в десятичных, а затем в обыкновенных дробях:
Г=°'5 1,45+0,5=1,95 Сначала учитель подсказывает учащимся, с какими дробями целесообразнее выполнять действия. По мере накопления опыта учащиеся сами должны выбирать наиболее удобные пути решения в каждом конкретном случае. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
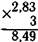

 Например: Х0,032 38
Например: Х0,032 38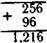




 1,45+^=?
1,45+^=?