
|
|
Акустические колебания с непрерывным спектром.Источники звука.
В принципе, источником звука может стать любое твердое тело, если возбудить в нем колебания. Например, постучать по нему. Источники звука как устройства, специально созданные для получения звука, изобретались и совершенствовались на протяжение всей истории человечества. По-видимому, одним из первых изобретений такого рода явился барабан, и успех этой затеи легко объясним: звук, возникающий при ударе по натянутой на барабан шкуре, хорошо соответствует возможностям нашего слуха, а большая поверхность шкуры обеспечивает большую энергию колебаний, звук получается громким и слышен далеко. Свою долгую историю имеют музыкальные инструменты, в число которых вошел, разумеется, и барабан. Развивался голосовой аппарат человека, совершенствовались навыки его использования. Свой путь стремительного развития прошла в двадцатом веке радиоаппаратура и электронно-акустическая техника, а также техника звукозаписи. С точки зрения теории колебаний, во всех источниках звука имеют место колебания двух видов: свободные и вынужденные. Рассмотрим сначала особенности свободных колебаний.
Свободные колебания.
В системе, выведенной из состояния равновесия, а затем предоставленной самой себе, устанавливаются свободные колебания некоторой строго определенной частоты ν0, которая называется собственной частотой колебаний данной системы. Так, для математического маятника собственная частота определяется длиной нити и ускорением свободного падения тел в данной местности:
Более сложные системы имеют не одно, а несколько значений собственной частоты: u1, u2, u3,… Применительно к источникам звука это следует понимать так: подобная система, выведенная из состояния равновесия, начинает звучать сразу на всех собственных частотах u1, u2, u3,… Возникает сложное колебательное движение как сумма простых синусоидальных колебаний. Примером такой системы является струна. Каждому натяжению струны соответствует свой ряд значений собственной частоты колебаний u1, u2, u3,... . Аналогично, ряд значений собственной частоты колебаний характерен для любого натяжения голосовых связок. Наименьшая частота u1 из этого ряда называется частотой основного тона, или просто тоном. Остальные частоты называются обертонами, и они связаны с основным тоном следующим образом: u2 = 2u1; u3 = 3u1; и т.д. Значения собственных частот часто называют так же «первая гармоника», «вторая гармоника», и т.д. Распределение общей энергии сложного колебания по различным гармоникам может быть самым разнообразным. Диаграмма, показывающая зависимость амплитуды А каждой гармоники от ее частоты называется спектром колебаний, и имеет следующий вид:
Спектр данного вида называется линейчатым. Информация о фазах колебаний в каждой гармонике на таких диаграммах не представлена. Да она, как оказалось, и не очень нужна. Как доказал Георг Симон Ом, наше восприятие сложного звука не зависит от разности фаз в гармониках. А вот как обстоят дела со свободными колебаниями в камертоне. Он применяется для настойки музыкальных инструментов, а так же и для «настройки» хора. Представляет собой U – образный стальной стержень прямоугольного поперечного сечения. Имеет ножку, за которую его можно держать. Начинает звучать, если его обо что-нибудь ударить. Является источником стандартного настроечного звука с частотой 440 Гц; высшие гармоники от него не требуются; более того, они не желательны. Однако, аппаратура для измерения энергии колебаний на различных частотах показала, что при ударе по камертону возникает несколько обертонов, но в этом устройстве они очень быстро затухают, оставляя лишь колебания основного тона, что от камертона и требуется. Воздушные столбы, ограниченные стенками, так же являются обладателями своего ряда собственных частот. Их собственные частоты – это частоты таких волн, для которых длина волны укладывается в длину воздушного столба целое число раз.
Проследим графически, как из двух простых колебаний получается сложное колебательное движение. На рис.2 слева представлен линейчатый спектр, имеющий гармоники u и 2u. Пусть амплитуды колебаний в этих гармониках равны, соответственно, А1 = 2 см и А2 = 1 см. Если на вход осциллографа подавать поочередно колебания частоты u и 2u, то мы вправе рассчитывать на получение на экране картинок (2а), а затем (2b). Сплошную кривую на графике (2с) можно рассматривать как прогноз: что должен показать осциллограф, если на его вход подать обе гармоники одновременно. Сплошная кривая получена простым суммированием ординат двух предыдущих графиков. Отчетливые точки на сплошной кривой соответствуют тем стадиям колебаний, когда суммирование ординат предельно упрощается. Мы получили картину сложных колебаний в пределах одного периода Т, который соответствует частоте u основного Рис. 2
тона: Т = 1/u. Мы шли от простых гармонических колебаний к сложной сумме. Подавая на вход осциллографа электрический сигнал от микрофона, «озвученного» каким-нибудь музыкальным звуком, мы получим на экране периодические кривые типа 2с, но более сложные в связи с большим числом гармоник. Оказалось возможным математическое решение обратной задачи: сложное колебание представить в виде суммы простых гармоник с любой требуемой точностью. Разложение Фурье.
Математическое представление сложных периодических колебаний в виде суммы простых гармоник называется разложением в ряд Фурье, любая периодическая функция времени f (t), имеющая период Т, может быть представлена в виде суммы простых гармоник следующего вида: f (t) = A0 + (A1 сos ωt + B1 sin ωt) + (A2 cos 2ωt + B2 sin 2ωt) +… (1) Здесь ω = 2π/Т – величина, называемая циклической частотой. Решить эту задачу для какой-нибудь конкретной функции f (t) – это значит найти для этой функции числовые значения коэффициентов (А0, А1, А2…) и (В1, В2…). В математике функциональный ряд – это, например, то, что записано в правой части формулы (1) с неограниченно большим (стремящимся к бесконечности) числом слагаемых. На практике этот бесконечный хвост слагаемых в правой части рано или поздно обрубают, и то, что остается, называется уже не рядом Фурье, а суммой Фурье. Если оказывается, что график суммы Фурье и график исходной функции f (t) отличаются слишком заметно, то сумму Фурье надо удлинить, вычислив еще пару коэффициентов Аk, Вk в дополнительное слагаемое (Ак cos kωt + Bk sin kωt). Действуя в таком духе, можно получить для любой функции f (t) приближенное математическое описание в виде суммы Фурье с любой желаемой точностью. Правда, полученная формула может оказаться громоздкой, но в наш компьютерный век эта беда – не беда. Весьма существенное обстоятельство: при вычислении дополнительных коэффициентов (Аk, Вk) не требуется пересмотра ранее вычисленных коэффициентов. В этом обзоре мы обходим стороной вопрос о том, как следует вычислять коэффициенты разложения (Аk, Вk). Отметим лишь, что они вычисляются интегрированием. Что и как нужно интегрировать, можно выяснить в справочной и специальной литературе. Разложение Фурье было предложено еще в начале 19 века, и с тех пор широко применяется. По этой причине разложение Фурье фигурирует и в учебных программах медицинских вузов. Этот мощный метод дает возможность представить любой сложный процесс в виде суммы гармоник различной амплитуды. Легко обходится даже требование о периодичности исходной функции f(t). А громоздкие процедуры по вычислению коэффициентов (Аk, Вk) в нынешние времена легко решаются обращением к соответствующей стандартной компьютерной программе. Однако есть в этом деле одна тонкость, которая нам представляется важной: метод Фурье может давать описание в виде суммы гармоник, которых в реальном процессе может и не быть. Например, на столбе висит фонарь, и он периодически то включается, то выключается. Получается, что освещенность под фонарем – это функция f (t) следующего вида:
0 t рис.3
Для этой функции можно получить разложение Фурье, и график полученной формулы может совпадать с графиком рис.3 с любой требуемой точностью, но метод Фурье здесь будет работать чисто формально. Интерпретировать гармоники такого формального разложения Фурье как совокупность неких реальных колебаний было бы совершенно некорректно. Другое дело – акустические колебания: сложный звук допускает разложение Фурье в виде (1), при этом гармоники разложения соответствуют реальным физическим процессам. Так, если частота основного тона струны u1 = 440 Гц, то при этом действительно возникают (экспериментально подтверждаются) гармоники с частотами u2 = 2u1 = 880 Гц, u3 = 3u1 = 1320 Гц, и т.д., потому что струна звучит как единое целое (440 Гц), но так же излучает дополнительный звук двумя половинами своей длины (880 Гц), и т.д. Потому что вдоль струны устанавливаются так называемые «стоячие волны», узлы которых разделяют струну на автономно и совместно звучащие участки.
Акустические колебания с непрерывным спектром.
Звуковые колебания с непрерывным спектром относятся к категории шумов. А у шумов – устойчивая репутация посторонних, ненужных звуков, от которых следует избавиться. Но это верно лишь отчасти. Произнося согласные, мы издаем звуки с непрерывным частотным спектром. Звучание духовых музыкальных инструментов инициируется шумовыми акустическими колебаниями, создаваемыми с помощью губ музыканта или специального язычка. Скрипка звучит благодаря скрипу (шуму), возникающему при трении смычка о струну. Если амплитуда колебаний в шуме на всех частотах в среднем одинакова, то такой шум называется белым. Произнося звук «Ф», мы создаем что-то близкое к белому шуму. Вопросы на засыпку: - В чем отличие чуть слышимого белого шума от белого шума, который мешает жить и работать? - В различных отраслях науки и техники есть проблема, которую можно обозначить так: «соотношение сигнал – шум». Как Вы понимаете сущность этой проблемы (на тех или иных частных примерах)? Что может мешать простому решению: шум отрезать, а сигнал оставить? Энергия колебаний может распределяться по частотам шума неравномерно. Например, акустический спектр при произнесении звука «С» примерно такой:
рис.4
Шумы как нежелательное явление, с которым приходится бороться, подразделяются на низкочастотные, среднечастотные и высокочастотные. Эти названия следует понимать так: в шуме представлены все частоты колебаний, но преобладают (имеют повышенную амплитуду) колебания низких, средних или высоких частот. Особо зловредными считаются высокочастотные шумы. Специфика их воздействия – в том, что спустя какое-то время мы их почти не замечаем, но эта защитная реакция организма не отменяет угнетающего действия такого шума на нервную систему, и угнетенное состояние постепенно усугубляется. А вот если кто-то пойдет и выключит источник такого шума, мы чувствуем резкое облегчение, и произносим что-то типа «Ах, как хорошо!» Стало быть, до этого было ах как плохо, но мы этого не замечали или почти не замечали. Шум может замедлять мыслительные процессы, увеличивать время реакции. Однако же и «гробовая тишина» – тоже не подарок. Испытания космонавтов в сурдокамере не считаются ими самым легким тестом. Выезжая «на природу», мы оказываемся вдали от шума городского, но в атмосфере слабых природных шумов листвы, воды и т.п., оказывающих весьма благотворное действие. Вопрос на засыпку: в чем особенности шума листвы в сравнении, например, с каким-нибудь техногенным шумом такого же уровня громкости? И заодно попытайтесь объяснить, почему мы смотрим на пламя костра как зачарованные? Обсудим вопрос о звуках с непрерывным спектром на частном примере произнесения звука «С». Здесь физическая картина событий такова: выдыхая воздух, мы с помощью языка, зубов, губ создаем на его пути преграды с достаточно резкими геометрическими формами. При обтекании таких преград течение воздушного потока становится турбулентным, т.е. вихревым. Появление вихрей становится неизбежным, если велики отличия в скорости смежных слоев потока, в данном случае газового. Что такое турбулентный вихрь? Это временный коллектив частиц, в котором происходит вращательное движение. Местные колебания давления в потоке возникают в связи с взаимодействием вихрей друг с другом, а так же на стадиях их возникновения и исчезновения. Хаотичная система возникающих и исчезающих вихрей различного масштаба приводит к разнообразным местным пульсациям давления в объеме потока, которым соответствует сложный звук с непрерывным спектром. Наличие максимума в непрерывном спектре рис.4 говорит о том, что при произнесении звука «С» в системе возникающих вихрей преобладают сравнительно крупные вихри, «работающие» на сравнительно низких частотах.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
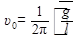
 А
А




 u1 u2 u3 u4 u5 u рис. 1
u1 u2 u3 u4 u5 u рис. 1
 f(t)
f(t)


