|
|
Раскрытие неопределенностей (Правило Лопиталя)Теорема о нахождении предела отношения функций через предел отношения производных Пусть функции 1) определены и дифференцируемы в некоторой проколотой окрестности точки 2) 3) существует 4) Тогда существует
Замечание. Правило Лопиталя можно рассматривать и в случае Доказательство. Рассмотрим случай Если Случай Замечания. 1.При применении правила Лопиталя дифференцируется числитель и знаменатель дроби отдельно. 2. Правило Лопиталя применяется только к дробям. Чтобы применить правило Лопиталя для неопределенностей вида Неопределенность Неопределенность
Неопределенности
Пример 4.5. Вычислить предел Решение. Пример 4.6. Вычислить предел Решение.
Пример 4.7. Вычислить предел Решение. Пример 4.8. Вычислить предел
Пример 4.9. Вычислить предел 3. Иногда правило Лопиталя применяется несколько раз, если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы должны оставаться справедливыми. Пример 4.10. Вычислить Решение.Значение предела
4.Правило Лопиталя не является универсальным, оно применимо лишь тогда, когда существует предел отношения производных Пример 4.11. Значение предела Формула Тейлора для многочленов В 1715 году Брук Тейлор[9] опубликовал формулу для разложения функции в степенной ряд, которая явилась мощным инструментом для исследования функций и приближенных вычислений. Рассмотрим вспомогательную задачу. Пусть функция
степени не выше
Будем искать
где коэффициенты Найдем производные многочлена
и далее,
Из (4.16) и (4.17) при
Отсюда
Значит, с учетом (4.15), должны выполняться равенства
Таким образом, поставленную задачу решает многочлен
Многочлен 4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано[10]
Покажем, что именно многочлен Тейлора Покажем, что В самом деле, рассмотрим т. е. Полученная формула носит название формулы Тейлора порядка В курсе математического анализа доказывается, что можно найти и другие погрешности приближения 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
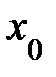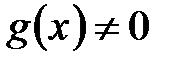и 
:
;
и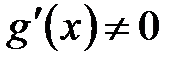 
в этой окрестности;
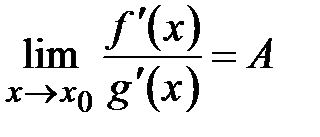(конечный или бесконечный);
или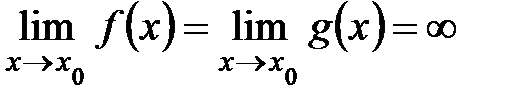 
.
, причем
.
. В этом случае достаточно сделать замену 
и воспользоваться результатом теоремы.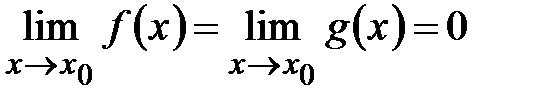
. Доопределим функци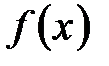и 
и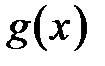 
в точке 
: 
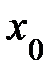и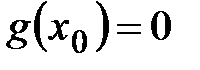 
. Так как теперь 
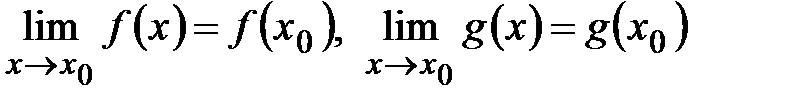, то функции 
и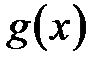 
будут непрерывны в точке 
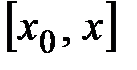, где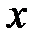 
– любая точка окрестности точки 
и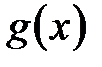 
непрерывны, дифференцируемы и 
. Поэтому применима теорема Коши: 
.
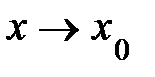, то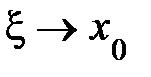 
и поэтому 
.
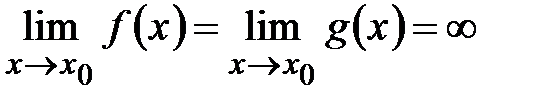оставляем без доказательства.
, 
, 
, 
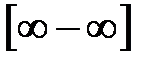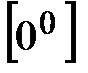и т. д., нужно предварительно исследуемое выражение преобразовать к дроби. Рассмотрим примеры раскрытия некоторых неопределенностей.
: 
.
:
.
.
.
.
.
.
.
.
.
. 
.
.
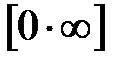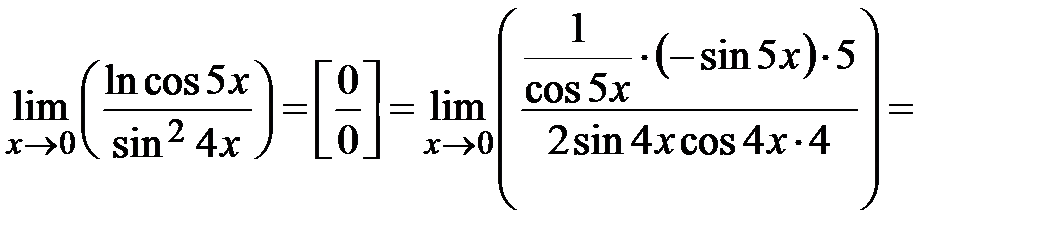
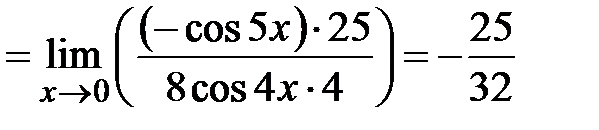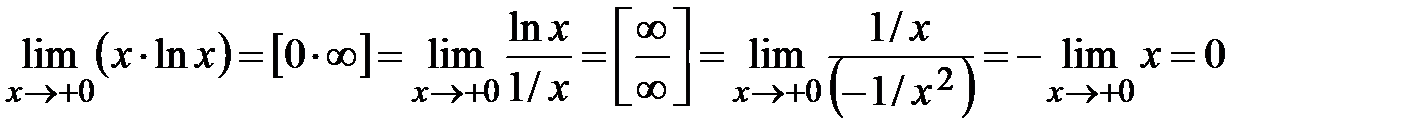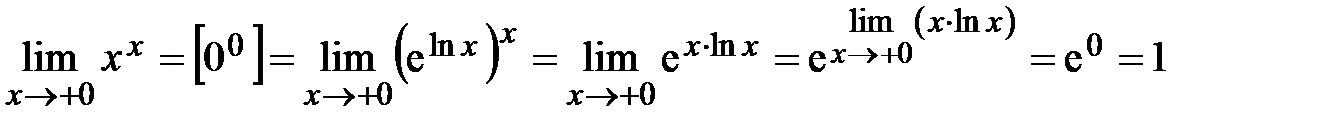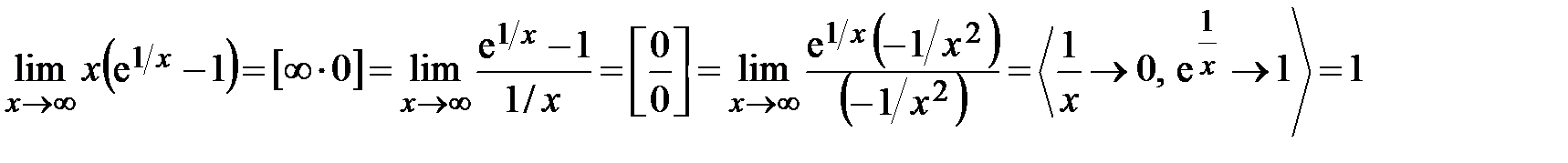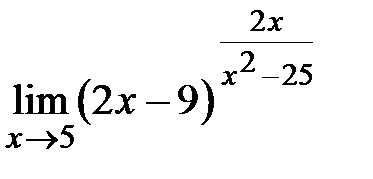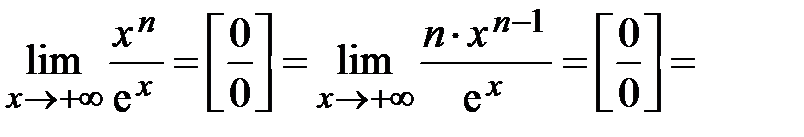
позволяет сравнить бесконечно большие при 
функции: показательная функция 
– бесконечно большая функция большего порядка по сравнению со степенной функцией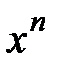 
– бесконечно большой при 
.
.
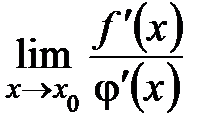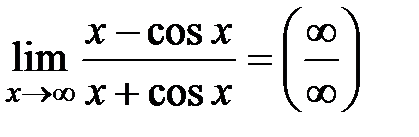получить по правилу Лопиталя нельзя, поскольку 
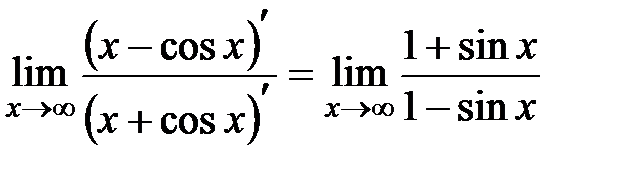– не существует ( 
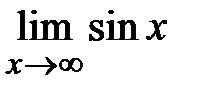не существует, см. решение примера 3.6). Однако исходный предел существует, его легко можно вычислить другим способом, например, так: 
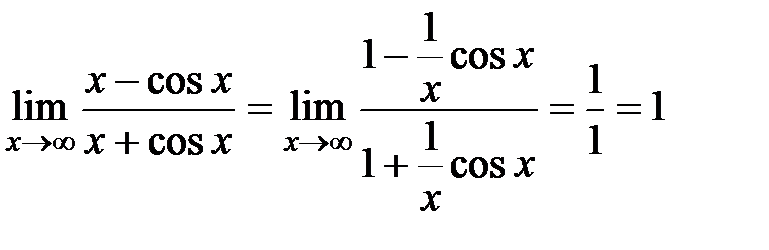, применяя теорему о пределе произведения бесконечно малой функции на ограниченную, в нашем случае, 
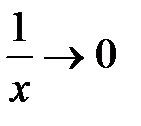при 
, 
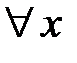имеет место неравенство 
.
имеет в окрестности точки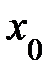 
производные до 
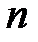- го порядка включительно. Требуется найти многочлен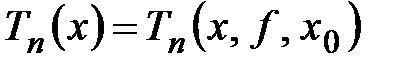
такой, что для всех 
выполняются равенства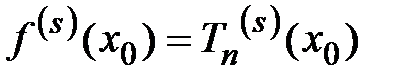
. (4.15)
в виде многочлена по степеням разности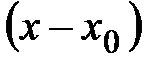 
:
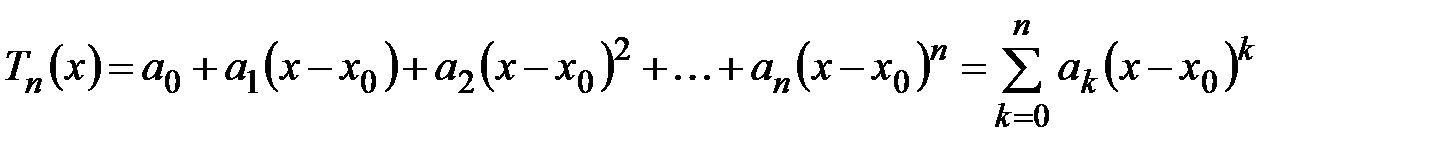, (4.16)
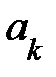нужно определить.
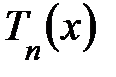порядка 
:
, 
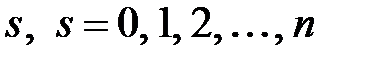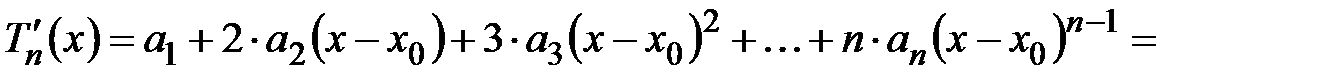
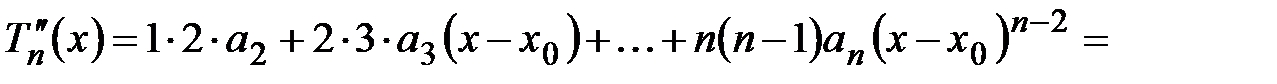(4.17)
,
.
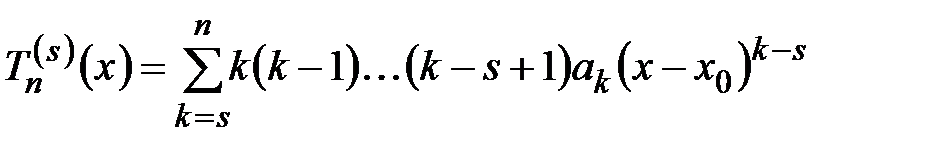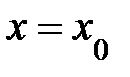получаем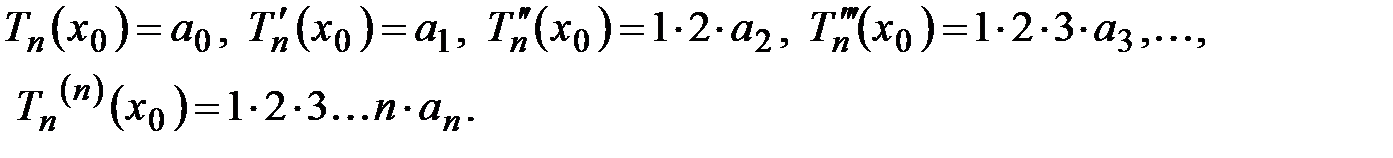
.
.
. (4.18)
, заданный формулой (4.18), называют многочленом Тейлора порядка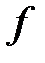 
в точке 
функции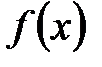 
задает наилучшее локальное приближение этой функции. Для этого оценим погрешность приближения 
, т. е. оценим в некоторой окрестности точки 
функцию 
. Разность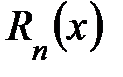 
называют остаточным членом формулы Тейлора.
.
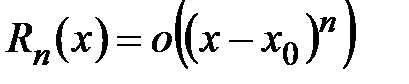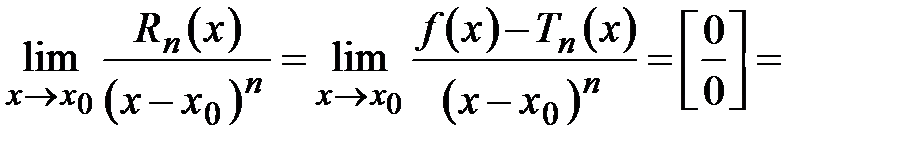(применим последовательно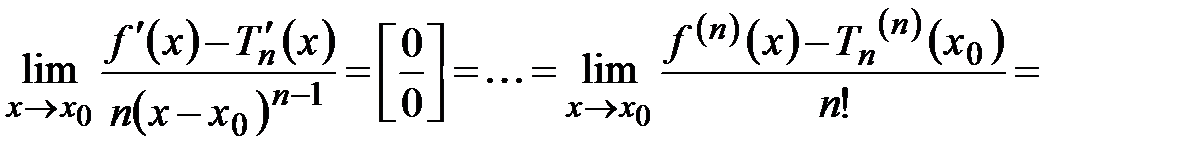 
а это означает, что 
,
. (4.19)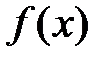
в окрестности точки 
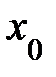. Формула (4.19) является качественной характеристикой погрешности.
.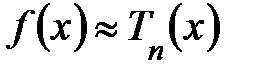