Определение функции, дифференцируемой в точке
Глава 3. Производная функции одной переменной
Производная функции в точке
Пустьфункция  определена на множестве определена на множестве  и и  – предельная точка множества Х. Напомним: для любой точки – предельная точка множества Х. Напомним: для любой точки  приращение приращение  определяется формулой определяется формулой  . Приращением функции . Приращением функции  в точке в точке  называется функция аргумента называется функция аргумента  : :
 . .
Определение.Если существует конечный предел
 , ,
то значение этого предела называют производной функции  в точке в точке  , обозначают , обозначают  или или  . .
Используются и другие символические обозначения производной:
 , ,  , ,  . .
Лагранж[1] Ньютон[2] Лейбниц [3]
Таким образом, по определению
 , (3.1) , (3.1)
где  . .
Пример 3.1. Найдем производную функции  в любой точке в любой точке  области определения: области определения:
 . .
Следовательно, функция  имеет в каждой точке имеет в каждой точке  производную производную  . .
Экономисты используют для обозначения производной также символ  (т. е. (т. е.  ) и термин маржинальное значение функции в точке ) и термин маржинальное значение функции в точке  . .
Физический смысл производной
Производная  – скорость изменения функции в точке – скорость изменения функции в точке  . В частности, если . В частности, если  – время, – время,  – координата точки, движущейся по прямой в момент – координата точки, движущейся по прямой в момент  , то , то  – мгновенная скорость точки в момент времени – мгновенная скорость точки в момент времени  . .
Геометрический смысл производной. Связь с существованием касательной
| Рис. 3.1. Геометрический смысл производной
| Пусть  график функции график функции  ; ;  , ,  – две точки графика функции – две точки графика функции  (рис. 3.1). (рис. 3.1).
Угол между секущей АВ и осью Ох обозначим  . .
Определение. Если существует  , то прямая , то прямая  с угловым коэффициентом с угловым коэффициентом  , проходящая через точку , проходящая через точку  , называется касательной к графику функции , называется касательной к графику функции  в точке в точке  . .
Теорема 3.1. График функции  имеет в точке имеет в точке  касательную тогда и только тогда, когда функция касательную тогда и только тогда, когда функция  имеет в точке имеет в точке  производную производную  . .
Доказательство.
Необходимость. Пусть  . Так как функция . Так как функция  непрерывна, то непрерывна, то  . Но . Но  . Поэтому . Поэтому  , то есть функция , то есть функция  имеет в точке имеет в точке  конечную производную конечную производную  . .
Достаточность. Если существует  , то есть , то есть  , то , то  . Так как функции . Так как функции  , ,  непрерывные, то непрерывные, то  , то есть существует касательная к графику функции в точке , то есть существует касательная к графику функции в точке  . .
Замечание. Так как  , то при , то при  получаем получаем  . .
Таким образом,  – это тангенс угла наклона касательной к графику функции – это тангенс угла наклона касательной к графику функции  в точке в точке  . .
Уравнения касательной и нормали
Найдем уравнение касательной. Будем искать его в виде  . Так как . Так как  , то , то  , откуда , откуда  . Поскольку угловой коэффициент касательной . Поскольку угловой коэффициент касательной  , то ее уравнение имеет вид , то ее уравнение имеет вид
 . .
Определение. Нормальной прямой (илинормалью)к графику функции  в точке в точке  называется прямая, проходящая через точку называется прямая, проходящая через точку  перпендикулярно касательной в этой точке. перпендикулярно касательной в этой точке.
Угловой коэффициент нормали связан с угловым коэффициентом касательной формулой
 . .
Уравнение нормали к графику функции в точке 
 . .
Бесконечные производные
Если функция  непрерывна в точке непрерывна в точке  и и  равен равен  или или  , то говорят, что функция , то говорят, что функция  имеет в точке имеет в точке  бесконечную производную (равную бесконечную производную (равную  или или  соответственно). В этом случае касательная к графику функции в точке соответственно). В этом случае касательная к графику функции в точке  параллельна оси параллельна оси  ( (  ), и так как она проходит через точку ), и так как она проходит через точку  , то ее уравнение имеет вид: , то ее уравнение имеет вид:  . .
Пример 3.2. Рассмотрим функцию  , ,  . Имеем . Имеем
Рис. 3.2. График функции 
|  – вертикальная касательная к графику функции (рис. 3.2). – вертикальная касательная к графику функции (рис. 3.2).
Рис. 3.3. График функции 
| Пример 3.3.Рассмотрим функцию  , ,  . Имеем: . Имеем:  . Следовательно, прямая . Следовательно, прямая  – вертикальная касательная к графику функции (рис. 3.3). – вертикальная касательная к графику функции (рис. 3.3).
Односторонние производные
Пусть  определена на множестве определена на множестве 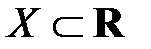 и и  – предельная точка – предельная точка   . .
Если существует конечный предел  , то его называют левой производной функции , то его называют левой производной функции  в точке в точке  и обозначают и обозначают  . . 
Аналогично  . Число . Число  (если оно существует), называется правой производной функции (если оно существует), называется правой производной функции  в точке в точке  . .
Теорема 3.2. Пусть  – предельная точка – предельная точка  . Функция . Функция  имеет производную в точке имеет производную в точке  тогда и только тогда, когда тогда и только тогда, когда  , ,  , причем , причем
 . .
Пример 3. 4.  . .  . .
Имеем:  , ,  . .
Так как  , функция , функция  не имеет производной в нуле. не имеет производной в нуле.
Пример 3.5.Пусть  . Выясним, существует ли производная этой функции в точке . Выясним, существует ли производная этой функции в точке  . .
Имеем:  . .
Итак, функция  в точке в точке  имеет производную имеет производную  . .
Пример 3.6. 
 , то есть , то есть  непрерывна в точке непрерывна в точке  . Однако . Однако
 не существует. Действительно, если не существует. Действительно, если  , а если , а если  . Следовательно, предел по Гейне не существует. . Следовательно, предел по Гейне не существует.
Дифференцируемость функции одной переменной
Определение функции, дифференцируемой в точке
Функция  , определенная на множестве , определенная на множестве  , называется дифференцируемой в точке , называется дифференцируемой в точке  , предельной для множества , предельной для множества  , если существует такая линейная относительно приращения , если существует такая линейная относительно приращения  функция функция 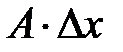 ( (  – некоторое число), что приращение – некоторое число), что приращение  функции функции  представимо в виде представимо в виде
 (3.2) (3.2)
где  . Так как . Так как  , то (3.2) можно записать в виде , то (3.2) можно записать в виде
 . .
Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
Для того чтобы функция  была дифференцируемой в точке была дифференцируемой в точке  , необходимо и достаточно, чтобы она имела в этой точке конечную производную. , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство.
Необходимость. Пусть функция  дифференцируема в точке дифференцируема в точке  . Тогда ее приращение можно представить в виде (3.2). Имеем . Тогда ее приращение можно представить в виде (3.2). Имеем
 . .
Следовательно, производная  существует и существует и  . .
Достаточность. Пусть существует конечная производная  . Тогда по определению производной . Тогда по определению производной  . Положим . Положим
 (3.3) (3.3)
Функция  является бесконечно малой при является бесконечно малой при  и непрерывной при и непрерывной при  . Действительно, . Действительно,  . Кроме того, из (3.3) вытекает . Кроме того, из (3.3) вытекает  . Тем самым доказано, что функция . Тем самым доказано, что функция  дифференцируема в точке дифференцируема в точке  . .
Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
Если функция  дифференцируема в точке дифференцируема в точке  , то она непрерывна в этой точке. , то она непрерывна в этой точке.
Доказательство. Из (3.2) вытекает равенство  , то есть функция , то есть функция  непрерывна в точке непрерывна в точке  . .
Обратное утверждение неверно. Непрерывность функции в точке является необходимым условием существования производной функции в этой точке, но не является достаточным.
В самом деле, пусть  . Функция . Функция  не имеет производной в нуле (пример 3.4), хотя она и непрерывна в любой точке не имеет производной в нуле (пример 3.4), хотя она и непрерывна в любой точке 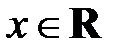 . .
Связь понятий: непрерывность функции, дифференцируемость функции, существование производной можно представить следующей схемой:
Функция дифференцируема в точке 
| | Функция непрерывна в точке x0
| Существует конечная производная 
|
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (т. е.
(т. е.  ) и термин маржинальное значение функции в точке
) и термин маржинальное значение функции в точке  .
.
 график функции
график функции  ;
;  ,
,  – две точки графика функции
– две точки графика функции  (рис. 3.1).
(рис. 3.1).
 – вертикальная касательная к графику функции (рис. 3.2).
– вертикальная касательная к графику функции (рис. 3.2).
 ,
,  . Имеем:
. Имеем:  . Следовательно, прямая
. Следовательно, прямая  – вертикальная касательная к графику функции (рис. 3.3).
– вертикальная касательная к графику функции (рис. 3.3).

 определена на множестве
определена на множестве  и
и  – предельная точка множества Х. Напомним: для любой точки
– предельная точка множества Х. Напомним: для любой точки  приращение
приращение  определяется формулой
определяется формулой  . Приращением функции
. Приращением функции  в точке
в точке  называется функция аргумента
называется функция аргумента  .
. ,
, в точке
в точке  , обозначают
, обозначают  или
или  .
. ,
,  ,
,  .
. , (3.1)
, (3.1) .
. в любой точке
в любой точке  области определения:
области определения: .
. .
. – скорость изменения функции в точке
– скорость изменения функции в точке  . В частности, если
. В частности, если  – время,
– время,  – координата точки, движущейся по прямой в момент
– координата точки, движущейся по прямой в момент  , то
, то  – мгновенная скорость точки в момент времени
– мгновенная скорость точки в момент времени  .
.


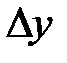




 .
.  , то прямая
, то прямая  с угловым коэффициентом
с угловым коэффициентом  , проходящая через точку
, проходящая через точку  , называется касательной к графику функции
, называется касательной к графику функции  в точке
в точке  .
. имеет в точке
имеет в точке  касательную тогда и только тогда, когда функция
касательную тогда и только тогда, когда функция  имеет в точке
имеет в точке  производную
производную  .
. . Так как функция
. Так как функция  непрерывна, то
непрерывна, то  . Но
. Но  . Поэтому
. Поэтому  , то есть функция
, то есть функция  имеет в точке
имеет в точке  конечную производную
конечную производную  .
. , то есть
, то есть  , то
, то  . Так как функции
. Так как функции  ,
,  непрерывные, то
непрерывные, то  , то есть существует касательная к графику функции в точке
, то есть существует касательная к графику функции в точке  .
. , то при
, то при  получаем
получаем  .
. – это тангенс угла наклона касательной к графику функции
– это тангенс угла наклона касательной к графику функции  в точке
в точке  .
. . Так как
. Так как  , то
, то  , откуда
, откуда  . Поскольку угловой коэффициент касательной
. Поскольку угловой коэффициент касательной  , то ее уравнение имеет вид
, то ее уравнение имеет вид .
. в точке
в точке  называется прямая, проходящая через точку
называется прямая, проходящая через точку  перпендикулярно касательной в этой точке.
перпендикулярно касательной в этой точке. .
.
 .
. непрерывна в точке
непрерывна в точке  и
и  равен
равен  или
или  , то говорят, что функция
, то говорят, что функция  имеет в точке
имеет в точке  параллельна оси
параллельна оси  (
(  ), и так как она проходит через точку
), и так как она проходит через точку  , то ее уравнение имеет вид:
, то ее уравнение имеет вид:  .
. ,
,  . Имеем
. Имеем

 определена на множестве
определена на множестве 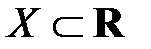 и
и  – предельная точка
– предельная точка 
 .
. , то его называют левой производной функции
, то его называют левой производной функции  в точке
в точке  и обозначают
и обозначают  .
. 
 . Число
. Число  (если оно существует), называется правой производной функции
(если оно существует), называется правой производной функции  .
. – предельная точка
– предельная точка  . Функция
. Функция  имеет производную в точке
имеет производную в точке  тогда и только тогда, когда
тогда и только тогда, когда  ,
,  , причем
, причем .
. .
.  .
. ,
,  .
. , функция
, функция  не имеет производной в нуле.
не имеет производной в нуле. . Выясним, существует ли производная этой функции в точке
. Выясним, существует ли производная этой функции в точке  .
. .
. в точке
в точке  .
.
 , то есть
, то есть  непрерывна в точке
непрерывна в точке  . Однако
. Однако не существует. Действительно, если
не существует. Действительно, если  , а если
, а если  . Следовательно, предел по Гейне не существует.
. Следовательно, предел по Гейне не существует. , определенная на множестве
, определенная на множестве  , называется дифференцируемой в точке
, называется дифференцируемой в точке  , предельной для множества
, предельной для множества  , если существует такая линейная относительно приращения
, если существует такая линейная относительно приращения  функция
функция 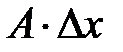 (
(  – некоторое число), что приращение
– некоторое число), что приращение  функции
функции  представимо в виде
представимо в виде (3.2)
(3.2) . Так как
. Так как  , то (3.2) можно записать в виде
, то (3.2) можно записать в виде .
. была дифференцируемой в точке
была дифференцируемой в точке  , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
, необходимо и достаточно, чтобы она имела в этой точке конечную производную. дифференцируема в точке
дифференцируема в точке  . Тогда ее приращение можно представить в виде (3.2). Имеем
. Тогда ее приращение можно представить в виде (3.2). Имеем .
. существует и
существует и  .
. . Тогда по определению производной
. Тогда по определению производной  . Положим
. Положим (3.3)
(3.3) является бесконечно малой при
является бесконечно малой при  и непрерывной при
и непрерывной при  . Действительно,
. Действительно,  . Кроме того, из (3.3) вытекает
. Кроме того, из (3.3) вытекает  . Тем самым доказано, что функция
. Тем самым доказано, что функция  дифференцируема в точке
дифференцируема в точке  .
. дифференцируема в точке
дифференцируема в точке  , то она непрерывна в этой точке.
, то она непрерывна в этой точке. , то есть функция
, то есть функция  непрерывна в точке
непрерывна в точке  . Функция
. Функция 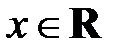 .
.