
|
|
Мощности, передаваемые валами
Мощности на валах:
P0= Pтр =9, 97 кВт
P1= P0
P2= P1 Крутящие моменты на валах Крутящие моменты, передаваемые валами, определяется по формуле Ti = 9550 Тогда T1=9550
T2=9550
T3=9550 Консольные нагрузки от муфт в кН предварительно определяют по ГОСТ 16162-85: на быстроходном валу Fк = (0.05…0.125) на тихоходном валу Fк =0.125
2. Расчет зубчатой передачи Исходные данные: Тип зуба – Косозубый Тип привода – Нереверсивный Крутящий момент на шестерне –500,4 Н м Частота вращения шестерни – n1=182,8 мин-1 Передаточное число u= 4 Режим работы – легкий Коэффициент использования передачи: в течение года – Kг =0.8 в течение суток – Kс =0.7 Cрок службы передачи в годах – L =5 Продолжительность включения – ПВ = 25 %
Выбор материалов зубчатых колес и способов термообработки
Материалы выбираем по табл. 1.1 [1] Шестерня Материал - сталь 40х. Термическая обработка - Закалка ТВЧ. Твердость поверхности зуба 45-50HRC Колесо Материал-сталь 40x. Термическая обработка - Улучшение. Твердость поверхности зуба HB 235-262. Расчет допускаемых контактных напряжений
Для их определения используем зависимость
где j=1 для шестерни, j=2 для колеса; sHlim j - предел контактной выносливости по табличным данным, sHlim1 = 2HB1+70=2•285.5+70=10007 МПа sHlim2= 2HB2+70=2•248.5+70=567 МПа SHj - коэффициент безопасности по табличным данным, SH1=1.2 SH2=1.1 KHLj - коэффициент долговечности; KHLj = здесь NH0j – базовое число циклов при действии контактных напряжений по табличным данным, NH01=73•106 NH02 =16.8•106 Эквивалентные числа циклов нагружения NHEj= Коэффициент эквивалентности при действии контактных напряжений определим по табличным данным в зависимости от режима нагружения: Суммарное время работы передачи в часах th = 365L24Kг Кс ПВ =365•5•24•0.8•0.7•0.25=6132 ч Суммарное число циклов нагружения NSi = 60• nj •c• th, где с – число зацеплений колеса за один оборот, с = 1; nj – частота вращения j-го колеса, n1=182 мин-1 n2= 61об/мин; NS1= 60•n•c•th =6.72•107 NS2= Эквивалентное число циклов контактных напряжений, NHE j= NHE1=8.40•106 NHE2= 2.102•106 Поскольку NHE1 >NH01, примем коэффициенты долговечности KHL1= 1.43 KHL2= Допускаемые контактные напряжения для шестерни и колеса
sHP1=
sHP2= Допускаемые контактные напряжения для косозубой передачи: sHP= 0.45 (sHP1 + sHP2) sHP= 0.45 (sHP1 + sHP2)= 869,7МПа s’HP=1.23sHPjmin=1.23•869,7 =1069,73 МПа Условие sHP
Допускаемые напряжения изгиба
где sF limj - предел выносливости зубьев при изгибе, взятый из табличных данных, sF lim 1 =1.75 HB1=1.75•285.5=600 МПа sF lim 2 =1.75 HB2=1.75•248.5=434,9 МПа SFj - коэффициент безопасности при изгибе, SF1=1.7 , SF2=1.7 ; KFCj - коэффициент, учитывающий влияние двухстороннего приложения нагрузки, (по табличным данным) KFC1=1 , KFC2=1 KFLj - коэффициент долговечности при изгибе: KFL j= здесь qj - показатели степени кривой усталости: q1 =6 , q2 =6 (по табличным данным). NF0 – базовое число циклов при изгибе; NF0 = 4•106. NFEj – эквивалентное число циклов напряжений при изгибе; NFE j= Коэффициент эквивалентности при действии напряжений изгиба определяется по табличным данным в зависимости от режима нагружения и способа термообработки
NFE1 = NFE2 = Так как NFE1 >NF0 ,то примем KFL1=1.157 KFL2 =1.358
Допускаемые напряжения изгиба:
Проектный расчет передачи
2.3.1. Межосевое расстояние
aw= Ka(u+1) где Ka=410 для косозубых передач. Коэффициент ширины зубчатого венца для косозубых передач примем ψba=0.4. На этапе проектного расчета задаемся значение коэффициента контактной нагрузки KH=1.2. Тогда aw= 160 мм, Полученное межосевое расстояние округлим до ближайшего большего стандартного значения, используя табличные данные: aw= 160 мм Рекомендуемый диапазон для выбора модуля mn=(0.01…0.02) aw=(0.01…0.02)125=1.25…2.5 мм Из полученного диапазона выбираем стандартный модуль mn=2 мм по табличным данным, учитывая, что для силовых передач модуль меньше 2 мм применять не рекомендуется. Суммарное число зубьев передачи Z где β1=0° для прямозубых передач, β1=12° для косозубых передач и β1=30° для шевронных передач. Полученное значение Z’∑ округлим до ближайшего целого числа Z∑=155 и определим делительный угол наклона зуба
Число зубьев шестерни
Z1= Число зубьев колеса Z2= Z Фактическое передаточное число uф = Значение uф не должно отличаться от номинального более чем на 3 % при u
Коэффициенты смещения шестерни и колеса примем x1= 0, x2= 0, 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
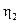
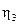 =9, 97•0.96•0.99=9, 47 кВт
=9, 97•0.96•0.99=9, 47 кВт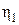
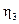 =4.12• 0.98• 0.99=9, 18 кВт
=4.12• 0.98• 0.99=9, 18 кВт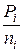 .
.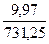 = 130,31 Н м
= 130,31 Н м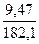 =500, 31 Н м
=500, 31 Н м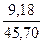 =1922, 51 Н м
=1922, 51 Н м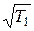 =1.557
=1.557 =5.551
=5.551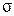 HPj =
HPj = 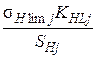
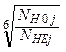
 1,
1, h •NSj
h •NSj
 =1.68•107
=1.68•107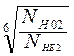 =
=  =1.41
=1.41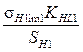 =
= 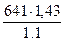 =1203,7 МПа
=1203,7 МПа =
= 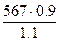 =729 МПа
=729 МПа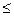 s’HP
s’HP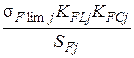 ,
,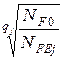
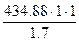 =408.4 МПа
=408.4 МПа =347.3 МПа
=347.3 МПа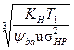 ,
,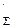 =
= 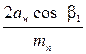 ,
,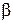 = arccos
= arccos 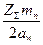
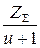 =31
=31 – Z1=126
– Z1=126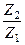 =4.065
=4.065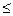 5.
5. u = 100
u = 100 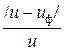 =100
=100 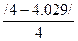 =0.007 % < 3 %
=0.007 % < 3 %