Хешированные таблицы и функции хеширования

Как отмечалось выше, в каждой реальной таблице фактическое множество ключей является лишь небольшим подмножеством множества всех теоретически возможных ключей. Поскольку память является одним из самых дорогостоящих ресурсов вычислительной системы, из соображений ее экономии целесообразно назначать размер пространства записей равным размеру фактического множества записей или превосходящим его незначительно. В этом случае мы должны иметь некоторую функцию, обеспечивающую отображение точки из пространства ключей в точку в пространстве записей, т.е. преобразование ключа в адрес записи: r = H(k), где - r адрес записи, k - ключ.

Такая функция называется функцией хеширования (другие ее названия - функция перемешивания, функция рандомизации).

При попытке отображения точек из некоторого широкого пространства в узкое неизбежны ситуации, когда разные точки в исходном пространстве отобразятся в одну и ту же точку в целевом пространстве. Ситуация, при которой разные ключи отображаются в один и тот же адрес записи, называется коллизией или переполнением, а такие ключи называются синонимами. Коллизии - основная проблема для хешированных таблиц, решение которой будет рассмотрено далее.

Если функция H, преобразующая ключ в адрес, может порождать коллизии, то однозначной обратной функции: k = H`(r), позволяющей восстановить ключ по известному адресу, существовать не может.

Поэтому ключ должен обязательно входить в состав записи хешированной таблицы как одно из ее полей.

К функции хеширования в общем случае предъявляются следующие требования:

* она должна обеспечивать равномерное распределение отображений фактических ключей по пространству записей;

* она должна порождать как можно меньше коллизий для данного фактического множества записей;

* она не должна отображать какую-либо связь между значениями ключей в связь между значениями адресов;

* она должна быть простой и быстрой для вычисления.

В книге Кнута приведен почти исчерпывающий обзор и анализ применяемых на практике функций хеширования, мы же ограничимся лишь обзором некоторых наиболее простых.

Простейшей функцией хеширования является деление по модулю числового значения ключа на размер пространства записи. Результат интерпретируется как адрес записи. Хотя эта функция и применяется во всех приводимых ниже примерах данного раздела, следует иметь в виду, что такая функция плохо соответствует первым трем требованиям к функции хеширования и сама по себе может быть применена лишь в очень ограниченном диапазоне реальных задач. Однако операция деления по модулю обычно применяется как последний шаг в более сложных функциях хеширования, обеспечивая приведение результата к размеру пространства записей.

Функция середины квадрата. Значение ключа преобразуется в число, это число затем возводится в квадрат, из него выбираются несколько средних цифр и интерпретируются как адрес записи.

Функция свертки. Цифровое представление ключа разбивается на части, каждая из которых имеет длину, равную длине требуемого адреса. Над частями производятся какие-то арифметические или поразрядные логические операции, результат которых интерпретируется как адрес. Например, для сравнительно небольших таблиц с ключами - символьными строками неплохие результаты дает функция хеширования, в которой адрес записи получается в результате сложения кодов символов, составляющих строку-ключ.

Функция преобразования системы счисления. Ключ, записанный как число в некоторой системе счисления P, интерпретируется как число в системе счисления Q>P. Обычно выбирают Q = P+1. Это число переводится из системы Q обратно в систему P, приводится к размеру пространства записей и интерпретируется как адрес.

3.9.4. Проблема коллизий в хешированных таблицах

Удачно подобранная функция хеширования может минимизировать число коллизий, но не может гарантировать их полного отсутствия.

Ниже мы рассмотрим методы разрешения проблемы коллизий в хешированных таблицах.

ПОВТОРНОЕ ХЕШИРОВАНИЕ. Повторное хеширование, известное также под названием открытой таблицы, предусматривает следующее: если при попытке записи в таблицу оказывается, что требуемое место в таблице уже занято, то значение записывается в ту же таблицу на какое-то другое место. Другое место определяется при помощи вторичной функции хеширования H2, аргументом которой в общем случае может быть и исходное значение ключа, и результат предыдущего хеширования:

r = H2(k,r`),

где r` - адрес, полученный при предыдущем применении функции хеширования. Если полученный в результате применения функции H2 адрес также оказывается занятым, функция H2 применяется повторно - до тех пор, пока не будет найдено свободное место. Простейшей функцией вторичного хеширования является функция:

r = r` + 1.

Эту функцию иногда называют функцией линейного опробования. Фактически при применении линейного опробования, если "законное" место записи (т.е. слот, расположенный по адресу, получаемому из первичной функции хеширования) уже занято, то запись занимает первое свободное место за "законным" (таблица при этом рассматривается как кольцо). Выборка элемента по ключу производится аналогичным образом: адрес записи вычисляется по первичной функции хеширования и ключ записи, расположенной по этому адресу, сравнивается с искомым. Если запись непуста и ключи не совпадают, то продолжается поиск с применением вторичной функции хеширования. Поиск заканчивается, когда найдена запись с искомым ключом (успешное завершение) или перебрана вся таблица (неуспешное завершение).

Приведенный ниже программный пример иллюстрирует применение метода линейного опробования для разрешения коллизий. В составляющем этот пример модуле определены процедуры/функции инициализации таблицы, вставки элемента в таблицу и поиска элемента в таблице. Процедура инициализации является обязательной для хешированных таблиц, так как перед началом работы с таблицей для нее должна быть выделена память и заполнена "пустыми" (свободными) записями. В качестве признака пустой записи значение ключа использована константа EMPTY, которая при отладке была определена как -1. Функция первичного хеширования - Hash - выполняет деление по модулю.

{==== Программный пример 3.19 ====}

{ Хешированная таблица с повторным перемешиванием }

Unit HashTbl;

Interface

Procedure Init;

Function Insert(key : integer) : boolean;

Function Fetch(key : integer) : integer;

Implementation

const N=...; { число записей в таблице }

type Seq = array[1..N] of integer; { тип таблицы }

var tabl : Seq; { таблица }

{ Хеширование - деление по модулю }

Function Hash(key : integer) : integer;

begin Hash:= key mod N+1; end;

{ Инициализация таблицы - заполнение пустыми записями }

Procedure Init;

var i : integer;

begin for i:=1 to N do tabl[i]:=EMPTY; end;

{ Добавление элемента в таблицу }

Function Insert(key : integer) : boolean;

Var addr, a1 : integer;

begin addr:=Hash(key); { вычисление адреса }

if tabl[addr]<>EMPTY then { если адрес занят }

begin a1:=addr;

repeat { поиск свободного места }

addr:=addr mod N+1;

until (addr=a1) or (tabl[addr]=EMPTY);

if tabl[addr]<>EMPTY then { нет свободного места }

begin Insert:=false; Exit; end;

end; tabl[addr]:=key; { запись в таблицу }

Insert:=true; end;

{ Выборка из таблицы - возвращает адрес найденного ключа

или EMPTY - если ключ не найден }

Function Fetch(key : integer) : integer;

Var addr, a1 : integer;

begin addr:=Hash(key);

if tabl[addr]=EMPTY then

Fetch:=EMPTY { место свободно - ключа нет в таблице }

else if tabl[addr]=key then

Fetch:=addr { ключ найден на своем месте }

else begin { место занято другим ключом }

a1:=(addr+1) mod N;

{ Поиск, пока не найден ключ или не сделан полный оборот }

while (tabl[a1]<>key) and (a1<>addr) do addr:=(a1+1) mod N;

if tabl[a1]<>key then Fetch:=EMPTY else Fetch:=a1;

end;

end.

Повторное хеширование обладает существенным недостатком: число коллизий зависит от порядка заполнения таблицы. Ниже приведен пример работы программы (пример 3.19) для двух случаев. В обоих случаях размер таблицы задавался равным 15. В первом случае в таблицу заносилась следующая последовательность из 14 чисел-ключей: 58 0 19 96 38 52 62 77 4 15 79 75 81 66

Результирующая таблица имела такой вид:

0 15* 62 77 19 4* 96 52 38 79* 75* 81* 66* 58 E

Буквой "E" обозначено свободное место в таблице. Значком "*" помечены элементы, стоящие не на своих "законных" местах. Во втором случае те же ключи заносились в таблицу в иной последовательности, а именно:

0 75 15 62 77 19 4 79 96 81 66 52 38 58

Результирующая таблица имела вид:

0 75* 15* 62* 77* 19* 4* 79* 96* 81* 66* 52* 38* 58 E

Большее число коллизий во втором случае объясняется тем, что если ключ не может быть записан по тому адресу, который вычислен для него первичной функцией хеширования, он записывается на свободное место, а это пока свободное место принадлежит (по первичной функции хеширования другому ключу, который впоследствии тоже может поступить на вход таблицы.

ПАКЕТИРОВАНИЕ. Сущность метода пакетирования состоит в том, что записи таблицы объединяются в пакеты фиксированного, относительно небольшого размера. Функция хеширования дает на выходе не адрес записи, а адрес пакета. После нахождения пакета в нем выполняется линейный поиск по ключу. Пакетирование позволяет сгладить нарушения равномерности распределения ключей по пространству пакетов и, следовательно, уменьшить число коллизий, но не может гарантированно их предотвратить. Пакеты также могут переполняться. Поэтому пакетирование применяется как дополнение к более радикальным методам - к методу повторного хеширования или к методам, описанным ниже. В программном примере 3.20 применен метод пакетирования без комбинации с другими методами. При общем размере таблицы - 15 и размере пакета - 3 уже ранее опробованная последовательность:

58 0 75 19 96 38 81 52 66 62 77 4 15 79

записывалась в результирующую таблицу без коллизий (значком "|" обозначены границы пакетов):

0 75 15| 96 81 66| 52 62 77| 58 38 E| 19 4 79

{==== Программный пример 3.20 ====}

{ Хешированная таблица с пакетами }

Unit HashTbl;

Interface

Procedure Init;

Function Insert(key : integer) : boolean;

Function Fetch(key : integer) : integer;

Implementation

const N=...; { число записей в таблице }

const NB=...; { размер пакета }

type Seq = array[1..N] of integer; { тип таблицы }

var tabl : Seq; { таблица }

{ Инициализация таблицы - заполнение пустыми записями }

Procedure Init;

var i : integer;

begin for i:=1 to N do tabl[i]:=EMPTY; end;

{ Хеширование - деление по модулю на число пакетов }

Function Hash(key : integer) : integer;

begin Hash:= key mod (N div NB); end;

{ Добавление элемента в таблицу }

Function Insert(key : integer) : boolean;

Var addr, a1, pa : integer;

begin pa:=Hash(key); { вычисление номера пакета }

addr:=pa*NB+1; { номер 1-го эл-та в пакете }

Insert:=true;

a1:=addr; { поиск свободного места в пакете }

while (a1<addr+NB) and (tabl[a1]<>EMPTY) do a1:=a1+1;

if a1<addr+NB then { своб.место найдено } tabl[a1]:=key

else { своб.место не найдено } Insert:=false;

end;

{ Выборка из таблицы }

Function Fetch(key : integer) : integer;

Var addr, a1 : integer;

begin

addr:=Hash(key)*NB+1; { номер 1-го эл-та в пакете }

a1:=addr; { поиск в пакете }

while (a1<addr+NB) and (tabl[a1]<>key) do a1:=a1+1;

if a1<addr+NB then Fetch:=a1 else Fetch:=EMPTY;

end;

END.

ОБЩАЯ ОБЛАСТЬ ПЕРЕПОЛНЕНИЙ. Для таблицы выделяются две области памяти: основная область и область переполнений. Функция хеширования на выходе дает адрес записи или пакета в основной области. При вставке записи, если ее "законное" место в основной области уже занято, запись заносится на первое свободное место в области переполнения. При поиске, если "законное" место в основной занято записью с другим ключом, выполняется линейный поиск в области переполнения. Программная иллюстрация приведена в примере 3.21.

При размере таблицы N=15 и размере области переполнения NPP=6 запись последовательности чисел:

58 0 75 82 96 38 88 52 66 62 78 4 15 79

дает такой вид таблицы (значком "|" показана граница между основной областью и областью переполнения):

0 -1 62 78 4 -1 96 82 38 -1 -1 -1 -1 58 -1 | 75 88 52 66 15 79

{==== Программный пример 3.21 ====}

{ Хешированная таблица с областью переполнения }

Unit HashTbl;

Interface

Procedure Init;

Function Insert(key : integer) : boolean;

Function Fetch(key : integer) : integer;

Implementation

const N=...; { число записей в таблице }

const NPP=...; { размер области переполнения }

type Seq = array[1..N+NPP] of integer; { тип таблицы - массив,

в котором первые N эл. составляют основную область, а следующие

NPP эл.тов - область переполнения }

var tabl : Seq; { таблица }

Procedure Init;{Инициализация таблицы - заполнение пустыми записями}

var i : integer;

begin for i:=1 to N+NPP do tabl[i]:=EMPTY; end;

{ Хеширование - деление по модулю }

Function Hash(key : integer) : integer;

begin Hash:= key mod N+1; end;

{ Добавление элемента в таблицу }

Function Insert(key : integer) : boolean;

Var addr : integer;

begin

addr:=Hash(key); { вычисление адреса }

Insert:=true;

if tabl[addr]=EMPTY then

{ если место в основной таблице свободно, то пишем на него }

tabl[addr]:=key

else begin { если место в основной таблице занято }

{ поиск свободного места в таблице переполнения }

addr:=N+1; { нач.адрес табл.переполнения }

while (tabl[addr]<>EMPTY) and (addr<N+NPP) do addr:=addr+1;

if tabl[addr]<>EMPTY then Insert:=false { нет места }

else tabl[addr]:=key; { запись в обл.переполнения }

end;

end;

Function Fetch(key : integer) : integer; { Выборка из таблицы }

Var addr : integer;

begin

addr:=Hash(key);

if tabl[addr]=key then { найден в основной таблице }

Fetch:=addr

else if tabl[addr]=EMPTY then { отсутствует в таблице }

Fetch:=EMPTY

else { линейный поиск в таблице переполнения }

begin addr:=N+1; { начало табл.переполнения }

while (addr<=N+NPP) and (tabl[addr]<>key) do addr:=addr+1;

if tabl[addr]<>key then {отсутствует в таблице} Fetch:=EMPTY

else { найден в таблице переполнения } Fetch:=addr;

end;

end;

END.

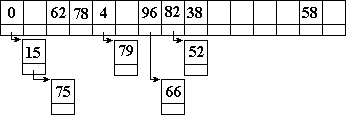
Общая область переполнений требует больше памяти, чем открытые таблицы: если размер открытой таблицы может не превышать размера фактического множества записей, то здесь еще требуется дополнительная память для переполнений. Однако эффективность доступа к таблице с областью переполнения выше, чем к таблице с повторным хешированием. Если в таблице с повторным хешированием при неудачной первой пробе приходится продолжать поиск во всей таблице, то в таблице с областью переполнения продолжение поиска ограничивается только областью переполнения, размер которой значительно меньше размера основной таблицы.

РАЗДЕЛЬНЫЕ ЦЕПОЧКИ ПЕРЕПОЛНЕНИЙ. Естественным представляется желание ограничить продолжение поиска лишь множеством тех значений ключей, которые претендуют на данное место в основной таблице. Эта идея реализуется в таблицах с цепочками переполнения. В структуру каждой записи добавляется еще одно поле - указатель на следующую запись. Через эти указатели записи с ключами-синонимами связываются в линейный список, начало которого находится в основной таблице, а продолжение - вне ее. При вставке записи в таблицу по функции хеширования вычисляется адрес записи (или пакета) в основной таблице. Если это место в основной таблице свободно, то запись заносится в основную таблицу. Если же место в основной таблице занято, то запись располагается вне ее. Память для такой записи с ключом-синонимом может выделяться либо динамически для каждой новой записи, либо для синонима назначается элемент из заранее выделенной области переполнения. После размещения записи-синонима поле указателя из записи основной таблицы переносится в поле указателя синонима, а на его место в записи основной таблицы записывается указатель на только что размещенный синоним.

Хотя в таблицах с цепочками переполнений и увеличивается размер каждой записи и несколько усложняется обработка за счет обработки указателей, сужение области поиска дает весьма значительный выигрыш в эффективности.

В программной иллюстрации примера 3.22 используется статическая область переполнения, элементы которой динамически распределяются по цепочкам. Роль указателя играют индексы в области переполнения. Специальное значение индекса EMPTY представляет пустой указатель.

При объеме основной области - 15 и области переполнения - 6 включение в таблицу следующей последовательности чисел:

58 0 75 82 96 38 88 52 66 62 78 4 15 79

привело к такому содержимому основной таблицы и области переполнения (каждый элемент представлен парой <число>:<указатель>, Е- пустое значение):

0:20 E:E 62:E 78:E 4:21 E:E 96:19 82:18 38:E E:E E:E

E:E E:E 58:17 E:E 75:E 88:E 52:E 66:E 15:16 79:E

Это содержимое таблицы с цепочками переполнения наглядно представлено на рис. 3.18.

Рис. 3.18. Цепочки переполнения

{==== Программный пример 3.22 ====}

{ Хешированная таблица с цепочками переполнений }

Unit HashTbl;

Interface

Procedure Init;

Function Insert(key : integer) : boolean;

Function Fetch(key : integer) : integer;

Implementation

const N=...; { число записей в таблице }

const NPP=...; { размер области переполнения }

type rec = record { запись таблицы }

key : integer; { ключ }

next : integer; { указатель на синоним }

end;

type Seq = array[1..N+NPP] of rec; { тип таблицы -

основная область и область переполнения }

var tabl : Seq; { таблица }

{ Хеширование - деление по модулю }

Function Hash(key : integer) : integer;

begin

Hash:= key mod N+1; end;

{ Инициализация таблицы - заполнение пустыми записями }

Procedure Init;

var i : integer;

begin

for i:=1 to N+NPP do

begin

tabl[i].key:=EMPTY; tabl[i].next:=EMPTY;

end;

end;

{ Добавление элемента в таблицу }

Function Insert(key : integer) : boolean;

Var addr1, addr2 : integer; {адреса- основной, переполнение}

begin

addr1:=Hash(key); { вычисление адреса }

Insert:=true;

if tabl[addr1].key=EMPTY then

{ эл-т в основной области свободен - запись в него }

tabl[addr1].key:=key

else { эл-т в основной области занят }

{ поиск свободного места в таблице переполнения }

begin addr2:=N+1;

while (tabl[addr2].key<>EMPTY) and (addr2<N+NPP) do

addr2:=addr2+1;

if tabl[addr2].key<>EMPTY then Insert:=false { нет места }

else { запись в область переполнения и

коррекция указателей в цепочке }

begin tabl[addr2].key:=key;

tabl[addr2].next:=tabl[addr1].next;

tabl[addr1].next:=addr2;

end;

end;

end;

Function Fetch(key : integer) : integer; { Выборка из таблицы }

Var addr : integer;

begin

addr:=Hash(key);

if tabl[addr].key=key then { найден на своем месте }

Fetch:=addr

else if tabl[addr].key=EMPTY then { нет в таблице }

Fetch:=EMPTY

else { поиск в таблице переполнения }

begin addr:=tabl[addr].next;

while (addr<>EMPTY) and (tabl[addr].key<>key) do

addr:=tabl[addr].next;

Fetch:=addr; { адрес в обл.переполнения или EMPTY }

end; end;

END.

При любом методе построения хешированных таблиц возникает проблема удаления элемента из основной области. Хотя эта глава и посвящена у нас статическим структурам данных, но в реальных задачах абсолютно неизменные структуры встречаются крайне редко.

При удалении удаляемая запись должна прежде всего быть найдена в таблице. Если запись найдена вторичным хешированием (открытая таблица) или в области переполнения (таблица с общей областью переполнения), то удаляемую запись достаточно пометить как пустую. Если запись найдена в цепочке (таблица с цепочками переполнений), то необходимо также скорректировать указатель предыдущего элемента в цепочке. Если же удаляемая запись находится на своем "законном" месте, то, пометив ее как пустую, мы тем самым сделаем невозможным поиск ее синонимом, возможно, имеющимся в таблице.

Одним из способов решения этой проблемы может быть пометка записи специальным признаком "удаленная". Этот способ часто применяется в таблицах с повторным хешированием и с общей областью переполнений, но он не обеспечивает ни освобождения памяти, ни ускорения поиска при уменьшении числа элементов в таблице. Другой способ - найти любой синоним удаляемой записи и перенести его на "законное" место. Этот способ легко реализуется в таблицах с цепочками, но требует значительных затрат в таблицах с другой структурой, так как требует поиска во всей открытой таблице или во всей области переполнения с вычислением функции хеширования для каждого проверяемого элемента.

Библиографический Список

1. Вирт Н. Алгоритмы и структуры данных /Н. Вирт. М.: Мир,1989.

2. Сибуя М. Алгоритмы обработки данных /М. Сибуя, Т. Ямамото. М.: Мир,1986.

3. Костин А.Е. Организация и обработка структур данных в вычислительных системах: учеб.пособ. для вузов /А.Е. Костин, В.Ф. Шаньгин . М.: Высш.шк., 1987.

4. Кнут Д. Искусство программирования для ЭВМ. Т.1: Основные алгоритмы: пер. с англ./Д. Кнут. М.: Мир,1978.

5. Кнут Д. Искусство программирования для ЭВМ.Т.3: Сортировка и поиск: пер. с англ./Д.Кнут. М.: Мир,1978.

6. Кормен Т. Алгоритмы: построение и анализ/ Т. Кормен, Ч. Лейзерсон, Р.Ривест. М.: МЦНМО, 2000.

ОГЛАВЛЕНИЕ

1. CТРУКТУРЫ ДАННЫХ И АЛГОРИТМЫ.. 3

1.1. Понятие структур данных и алгоритмов. 3

1.2. Алгоритм Евклида. 6

1.3. Классификация структур данных. 7

1.4. Операции над структурами данных. 10

1.5. Структурность данных и технология программирования. 11

2. ПРОСТЫЕ СТРУКТУРЫ ДАННЫХ.. 15

2.1. Числовые типы.. 16

2.1.1. Целые типы.. 16

2.1.2. Вещественные типы.. 21

2.1.3. Десятичные типы.. 27

2.1.4. Операции над числовыми типами. 28

2.2. Битовые типы.. 29

2.3. Логический тип. 30

2.4. Символьный тип. 31

2.5. Перечислимый тип. 32

2.6. Интервальный тип. 33

2.7. Указатели. 34

2.7.1. Физическая структура указателя. 35

2.7.2. Представление указателей в языках программирования. 36

2.7.3. Операции над указателями. 36

3. СТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ.. 36

3.1. Векторы.. 36

3.2. Массивы.. 36

3.2.1. Логическая структура. 36

3.2.2. Физическая структура. 36

3.2.3. Операции. 36

3.2.4. Адресация массивов с помощью векторов Айлиффа. 36

3.2.5. Специальные массивы.. 36

3.3. Множества. 36

3.3.1. Числовые множества. 36

3.3.2. Символьные множества. 36

3.3.3. Множество из элементов перечислимого типа. 36

3.3.4. Множество от интервального типа. 36

3.3.5. Операции над множествами. 36

3.4. Записи. 36

3.4.1. Логическое и машинное представление записей. 36

3.4.2. Операции над записями. 36

3.5. Записи с вариантами. 36

3.6. Таблицы.. 36

3.7. Операции логического уровня над статическими структурами. Поиск. 36

3.7.1. Последовательный или линейный поиск. 36

3.7.2. Бинарный поиск. 36

3.8. Операции логического уровня над статическими структурами. Сортировка 36

3.8.1. Сортировки выборкой. 36

3.8.2. Сортировки включением. 36

3.8.3. Сортировки распределением. 36

3.9. Прямой доступ и хеширование. 36

3.9.1. Таблицы прямого доступа. 36

3.9.2. Таблицы со справочниками. 36

3.9.3. Хешированные таблицы и функции хеширования. 36

3.9.4. Проблема коллизий в хешированных таблицах. 36

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 36

ОГЛАВЛЕНИЕ. 36

Не нашли, что искали? Воспользуйтесь поиском по сайту: