Адресация массивов с помощью векторов Айлиффа

Из вышеприведенных формул видно, что вычисление адреса элемента многомерного массива может потребовать много времени, поскольку при этом должны выполняться операции сложения и умножения, число которых пропорционально размерности массива. Операцию умножения можно исключить, если применять следующий метод.

Для массива любой мерности формируется набор дескрипторов: основного и несколько уровней вспомогательных дескрипторов, называемых векторами Айлиффа. Каждый вектор Айлиффа определённого уровня содержит указатель на нулевые компоненты векторов Айлиффа следующего, более низкого уровня, а векторы Айлиффа самого нижнего уровня содержат указатели групп элементов отображаемого массива. Основной дескриптор массива хранит указатель вектора Айлиффа первого уровня. При такой организации к произвольному элементу В(j1,j2,...,jn) многомерного массива можно обратиться пройдя по цепочке от основного дескриптора через соответствующие компоненты векторов Айлиффа.

На рис. 3.4 приведена физическая структура трёхмерного массива В[4..5,-1..1,0..1], представленная по методу Айлиффа. Из этого рисунка видно, что метод Айлиффа, увеличивая скорость доступа к элементам массива, приводит в то же время к увеличению суммарного объёма памяти, требуемого для представления массива. В этом заключается основной недостаток представления массивов с помощью векторов Айлиффа.

Рис. 3.4. Представление массивов с помощью векторов Айлиффа

Специальные массивы

На практике встречаются массивы, которые в силу определенных причин могут записываться в память не полностью, а частично. Это особенно актуально для массивов настолько больших размеров, что для их хранения в полном объеме памяти может быть недостаточно. К таким массивам относятся симметричные и разреженные массивы.

СИММЕТРИЧНЫЕ МАССИВЫ. Двумерный массив, в котором количество строк равно количеству столбцов, называется квадратной матрицей.

Квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, попарно равны друг другу, называется симметричной. Если матрица порядка n симметрична, то в ее физической структуре достаточно отобразить не n², а лишь n*(n+1)/2 её элементов. Иными словами, в памяти необходимо представить только верхний (включая и диагональ) треугольник квадратной логической структуры. Доступ к треугольному массиву организуется таким образом, чтобы можно было обращаться к любому элементу исходной логической структуры, в том числе и к элементам, значения которых хотя и не представлены в памяти, но могут быть определены на основе значений симметричных им элементов.

На практике для работы с симметричной матрицей разрабатываются следующие процедуры для:

а) преобразования индексов матрицы в индекс вектора,

б) формирования вектора и записи в него элементов верхнего треугольника элементов исходной матрицы,

в) получения значения элемента матрицы из ее упакованного представления. При таком подходе обращение к элементам исходной матрицы выполняется опосредованно, через указанные функции.

РАЗРЕЖЕННЫЕ МАССИВЫ. Разреженный массив - массив, большинство элементов которого равны между собой, так что хранить в памяти достаточно лишь небольшое число значений, отличных от основного (фонового) значения остальных элементов.

Различают два типа разреженных массивов:

1) массивы, в которых местоположения элементов со значениями, отличными от фонового, могут быть математически описаны;

2) массивы со случайным расположением элементов.

В случае работы с разреженными массивами вопросы размещения их в памяти реализуются на логическом уровне с учетом их типа.

МАССИВЫ С МАТЕМАТИЧЕСКИМ ОПИСАНИЕМ МЕСТОПОЛОЖЕНИЯ НЕФОНОВЫХ ЭЛЕМЕНТОВ. К данному типу массивов относятся массивы, у которых местоположения элементов со значениями, отличными от фонового, могут быть математически описаны, т.е. в их расположении есть какая-либо закономерность.

Элементы, значения которых являются фоновыми, называют нулевыми; элементы, значения которых отличны от фонового, - ненулевыми. Но нужно помнить, что фоновое значение не всегда равно нулю.

Ненулевые значения хранятся, как правило, в одномерном массиве, а связь между местоположением в исходном, разреженном, массиве и в новом, одномерном, описывается математически с помощью формулы, преобразующей индексы массива в индексы вектора.

На практике для работы с разреженным массивом разрабатываются такие функции:

а) для преобразования индексов массива в индекс вектора;

б) для получения значения элемента массива из ее упакованного представления по двум индексам (строка, столбец);

в) для записи значения элемента массива в ее упакованное представление по двум индексам.

При таком подходе обращение к элементам исходного массива выполняется с помощью указанных функций. Например, пусть имеется двумерная разреженная матрица, в которой все ненулевые элементы расположены в шахматном порядке, начиная со второго элемента. Для такой матрицы формула вычисления индекса элемента в линейном представлении будет следующей :

L=((y-1)*XM+x)/2),

где L - индекс в линейном представлении;

x, y - соответственно строка и столбец в двумерном представлении;

XM - количество элементов в строке исходной матрицы.

В программном примере 3.1 приведен модуль, обеспечивающий работу с такой матрицей (предполагается, что размер матрицы XM заранее известен).

{=====Программный пример 3.1=====}

Unit ComprMatr;

Interface

Function PutTab(y,x,value : integer) : boolean;

Function GetTab(x,y: integer) : integer;

Implementation

Const XM=...;

Var arrp: array[1..XM*XM div 2] of integer;

Function NewIndex(y, x : integer) : integer;

var i: integer;

begin NewIndex:=((y-1)*XM+x) div 2); end;

Function PutTab(y,x,value : integer) : boolean;

begin

if NOT ((x mod 2<>0) and (y mod 2<>0)) or

NOT ((x mod 2=0) and (y mod 2=0)) then begin

arrp[NewIndex(y,x)]:=value; PutTab:=true; end

else PutTab:=false;

end;

Function GetTab(x,y: integer) : integer;

begin

if ((x mod 2<>0) and (y mod 2<>0)) or

((x mod 2=0) and (y mod 2=0)) then GetTab:=0

else GetTab:=arrp[NewIndex(y,x)];

end;

end.

Сжатое представление матрицы хранится в векторе arrp.

Функция NewIndex выполняет пересчет индексов по вышеприведенной формуле и возвращает индекс элемента в векторе arrp.

Функция PutTab выполняет сохранение в сжатом представлении одного элемента с индексами x, y и значением value. Сохранение выполняется только в том случае, если индексы x, y адресуют заведомо ненулевой элемент. Если сохранение выполнено, функция возвращает true, иначе - false.

Для доступа к элементу по индексам двумерной матрицы используется функция GetTab, которая по индексам x, y возвращает выбранное значение. Если индексы адресуют заведомо нулевой элемент матрицы, функция возвращает 0.

Обратите внимание на то, что массив arrp, а также функция NewIndex не описаны в секции IMPLEMENTATION модуля. Доступ к содержимому матрицы извне возможен только через входные точки PutTab, GetTab с заданием двух индексов.

В программном примере 3.2 та же задача решается несколько иным способом: для матрицы создается дескриптор - массив desc, который заполняется при инициализации матрицы таким образом, что i-й элемент массива desc содержит индекс первого элемента i-й строки матрицы в ее линейном представлении. Процедура инициализации InitTab включена в число входных точек модуля и должна вызываться перед началом работы с матрицей. Но доступ к каждому элементу матрицы (функция NewIndex) упрощается и выполняется быстрее: по номеру строки y из дескриптора сразу выбирается индекс начала строки и к нему прибавляется смещение элемента из столбца x. Процедуры PutTab и GetTab - такие же, как и в примере 3.1 поэтому здесь не приводятся.

{=====Программный пример 3.2=====}

Unit ComprMatr;

Interface

Function PutTab(y,x,value : integer) : boolean;

Function GetTab(x,y: integer) : integer;

Procedure InitTab;

Implementation

Const XM=...;

Var arrp: array[1..XM*XM div 2] of integer;

desc: array[1..XM] of integer;

Procedure InitTab;

var i : integer;

begin

desc[1]:=0; for i:=1 to XM do desc[i]:=desc[i-1]+XM; end;

Function NewIndex(y, x : integer) : integer;

var i: integer;

begin NewIndex:=desc[y]+x div 2; end;

end.

РАЗРЕЖЕННЫЕ МАССИВЫ СО СЛУЧАЙНЫМ РАСПОЛОЖЕНИЕМ ЭЛЕМЕНТОВ. К данному типу массивов относятся массивы, у которых местоположения элементов со значениями, отличными от фонового, не могут быть математически описаны, т.е. в их расположении нет какой-либо закономерности.

0 0 6 0 9 0 0 Пусть есть матрица А размерности 5*7, в которой

2 0 0 7 8 0 4 из 35 элементов только 10 отличны от нуля.

10 0 0 0 0 0 0

0 0 12 0 0 0 0

0 0 0 3 0 0 5

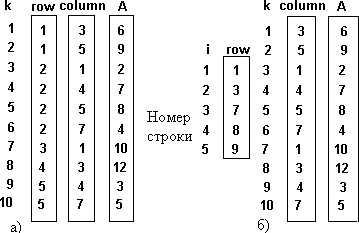
ПРЕДСТАВЛЕНИЕ РАЗРЕЖЕННЫХ МАТРИЦ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОГО РАЗМЕЩЕНИЯ. Один из основных способов хранения подобных разреженных матриц заключается в запоминании ненулевых элементов в одномерном массиве и идентификации каждого элемента массива индексами строки и столбца, как на рис. 3.5, а.

Доступ к элементу массива A с индексами i и j выполняется выборкой индекса i из вектора ROW, индекса j из вектора COLUM и значения элемента из вектора A. Слева указан индекс k векторов, наибольшее значение которого определяется количеством нефоновых элементов. Отметим, что элементы массива обязательно запоминаются в порядке возрастания номеров строк.

Более эффективное представление, с точки зрения требований к памяти и времени доступа к строкам матрицы, показано на рис. 3.5,б. Вектор ROW уменьшен, количество его элементов соответствует числу строк исходного массива A, содержащих нефоновые элементы. Этот вектор получен из вектора ROW рис. 3.5,а так, что его i-й элемент является индексом k для первого нефонового элемента i-й строки.

Рис. 3. 5. Последовательное представление разреженных матриц

Представление матрицы А, данное на рис. 3.5, сокращает требования к объему памяти более чем в 2 раза. Для больших матриц экономия памяти очень важна. Способ последовательного распределения имеет также то преимущество, что операции над матрицами могут быть выполнены быстрее, чем это возможно при представлении в виде последовательного двумерного массива, особенно если размер матрицы велик.

ПРЕДСТАВЛЕНИЕ РАЗРЕЖЕННЫХ МАТРИЦ МЕТОДОМ СВЯЗАННЫХ СТРУКТУР. Методы последовательного размещения для представления разреженных матриц обычно позволяют быстрее выполнять операции над матрицами и более эффективно использовать память, чем методы со связанными структурами. Однако последовательное представление матриц имеет определенные недостатки. Так, включение и исключение новых элементов матрицы вызывает необходимость перемещения большого числа других элементов. Если включение новых элементов и их исключение осуществляется часто, то должен быть выбран описываемый ниже метод связанных структур.

Метод связанных структур, однако, переводит представляемую структуру данных в другой раздел классификации. При этом логическая структура данных остается статической, а физическая структура становится динамической.

Рис. 3.6. Формат вершины для представления разреженных матриц

Для представления разреженных матриц требуется базовая структура вершины (рис.3.6), называемая MATRIX_ELEMENT ("элемент матрицы"). Поля V, R и С каждой из этих вершин содержат соответственно значение, индексы строки и столбца элемента матрицы. Поля LEFT и UP являются указателями на следующий элемент для строки и столбца в циклическом списке, содержащем элементы матрицы. Поле LEFT указывает на вершину со следующим наименьшим номером строки.

На рис. 3.7 приведена многосвязная структура, в которой используются вершины такого типа для представления матрицы А, описанной ранее в данном пункте. Циклический список представляет все строки и столбцы. Список столбца может содержать общие вершины с одним списком строки или более. Для того чтобы обеспечить использование более эффективных алгоритмов включения и исключения элементов, все списки строк и столбцов имеют головные вершины.

Головная вершина каждого списка строки содержит нуль в поле С; аналогично каждая головная вершина в списке столбца имеет нуль в поле R. Строка или столбец, содержащие только нулевые элементы, представлены головными вершинами, у которых поле LEFT или UP указывает само на себя. Может показаться странным, что указатели в этой многосвязной структуре направлены вверх и влево, вследствие чего при сканировании циклического списка элементы матрицы встречаются в порядке убывания номеров строк и столбцов. Такой метод представления используется для упрощения включения новых вершин в структуру.

Рис. 3.7. Многосвязная структура для представления матрицы А

Предполагается, что новые вершины, которые должны быть добавлены к матрице, обычно располагаются в порядке убывания индексов строк и индексов столбцов. Если это так, то новая вершина всегда добавляется после головной и не требуется никакого просмотра списка.

Множества

ЛОГИЧЕСКАЯ СТРУКТУРА. Множество - такая структура, которая представляет собой набор неповторяющихся данных одного и того же типа. Множество может принимать все значения базового типа. Базовый тип не должен превышать 256 возможных значений. Поэтому базовым типом множества могут быть byte, char и производные от них типы.

ФИЗИЧЕСКАЯ СТРУКТУРА. Множество в памяти хранится как массив битов, в котором каждый бит указывает, является ли элемент принадлежащим объявленному множеству или нет. Т.о. максимальное число элементов множества 256, а данные типа множество могут занимать не более 32 байт (пример 3.3).

Число байтов, выделяемых для данных типа множество, вычисляется по формуле:

ByteSize = (max div 8)-(min div 8) + 1,

где max и min - верхняя и нижняя границы базового типа данного множества.

Номер байта для конкретного элемента Е вычисляется по формуле:

ByteNumber = (E div 8)-(min div 8),

номер бита внутри этого байта по формуле:

BitNumber = E mod 8

{=====Программный пример 3.3=====}

const max=255; min=0; E=13;

var S : set of byte;

ByteSize, ByteNumb, BitNumb : byte;

begin

S:=[]; { обнуление множества }

S:=S+[E]; { запись числа в множество }

ByteSize:=(max div 8)-(min div 8)+1;

Bytenumb:=(E div 8)-(min div 8); BitNumb:=E mod 8;

writeln(bytesize); { на экране 32 }

writeln(bytenumb); { на экране 1 }

writeln(bitnumb); { на экране 5 }

end.

Числовые множества

Стандартный числовой тип, который может быть базовым для формирования множества, - тип byte.

Множество хранится в памяти как показано в табл. 3.3.

Таблица 3.3

В таблице : @S - адрес данного типа множества.

Бит поля установлен в 1, если элемент входит в множество, и в 0 - если не входит.

Например: S : set of byte; S:=[15,19];

Содержимое памяти при этом будет следующим:

@S+0 - 00000000 @S+2 - 00001000

@S+1 - 10000000 . . . . . @S+31 – 00000000

Символьные множества

Символьные множества хранятся в памяти так же, как и числовые множества. Разница лишь в том, что хранятся не числа, а коды ASCII символов.

Например: S : set of char; S:=['A','C'];

В этом случае представление множества S в памяти выглядит следующим образом :

@S+0 - 00000000 . . . . .

. . . . . . @S+31 - 00000000

@S+8 - 00001010

Не нашли, что искали? Воспользуйтесь поиском по сайту: