
|
|
Статические структуры данных
Статические структуры относятся к разряду непримитивных структур, которые, фактически, представляют собой структурированное множество примитивных, базовых, структур. Например, вектор может быть представлен упорядоченным множеством чисел. Поскольку по определению статические структуры отличаются отсутствием изменчивости, память для них выделяется автоматически - как правило, на этапе компиляции или при выполнении - в момент активизации того программного блока, в котором они описаны. Ряд языков программирования допускают размещение статических структур в памяти на этапе выполнения по явному требованию программиста, но и в этом случае объем выделенной памяти остается неизменным до уничтожения структуры. Выделение памяти на этапе компиляции является столь удобным свойством статических структур, что в ряде задач программисты используют их даже для представления объектов, обладающих изменчивостью. Например, когда размер массива неизвестен заранее, для него резервируется максимально возможный размер. Каждую структуру данных характеризуют её логическим и физическим представлениями. Очень часто говоря о той или иной структуре данных, имеют в виду её логическое представление. Физическое представление обычно не соответствует логическому и, кроме того, может существенно различаться в разных программных системах. Нередко физической структуре ставится в соответствие дескриптор, или заголовок, который содержит общие сведения о физической структуре. Дескриптор необходим, например, в том случае, когда граничные значения индексов элементов массива неизвестны на этапе компиляции, и, следовательно, выделение памяти для массива может быть выполнено только на этапе выполнения программы . Дескриптор хранится, как и сама физическая структура, в памяти и состоит из полей, характер, число и размеры которых зависят от той структуры, которую он описывает, и от принятых способов ее обработки. В ряде случаев дескриптор является совершенно необходимым, так как выполнение операции доступа к структуре требует обязательного знания каких-то ее параметров, и эти параметры хранятся в дескрипторе. Другие хранимые в дескрипторе параметры не являются совершенно необходимыми, но их использование позволяет сократить время доступа или обеспечить контроль правильности доступа к структуре. Дескриптор структуры данных, поддерживаемый языками программирования, является "невидимым" для программиста; он создается компилятором и компилятор же, формируя объектные коды для доступа к структуре, включает в эти коды команды, обращающиеся к дескриптору. Статические структуры в языках программирования связаны со структурированными типами. Структурированные типы в языках программирования являются теми средствами интеграции, которые позволяют строить структуры данных сколь угодно большой сложности. К таким типам относятся: массивы, записи (в некоторых языках - структуры) и множества (этот тип реализован не во всех языках). Векторы ЛОГИЧЕСКАЯ СТРУКТУРА. Вектор (одномерный массив) - структура данных с фиксированным числом элементов одного и того же типа. Каждый элемент вектора имеет уникальный в рамках заданного вектора номер. Обращение к элементу вектора выполняется по имени вектора и номеру требуемого элемента. МАШИННОЕ ПРЕДСТАВЛЕНИЕ. АДРЕСАЦИЯ ЭЛЕМЕНТОВ СТРУКТУР. Элементы вектора размещаются в памяти в подряд расположенных ячейках памяти. Под элемент вектора выделяется количество байт памяти, определяемое базовым типом элемента этого вектора. Необходимое число байтов памяти для хранения одного элемента вектора называется слотом. Размер памяти для хранения вектора определяется произведением длины слота на число элементов. В языках программирования вектор представляется одномерным массивом с синтаксисом описания вида (PASCAL): <Имя> : array [n..k] of <тип>; где n - номер первого элемента, k - номер последнего элемента. Представление в памяти вектора будет такое, как показано на рис. 3.1.
Рис. 3.1. Представление вектора в памяти
Здесь @ Имя - адрес вектора или, что то же самое, адрес первого элемента вектора, Sizeof(тип) - размер слота (количество байт памяти для записи одного элемента вектора), (k-n)*Sizeof(тип) - относительный адрес элемента с номером k, или, что то же самое, смещение элемента с номером k. Например: var m1:array[-2..2] of real; представление данного вектора в памяти будет как на рис. 3.2.
Рис. 3.2. Представление вектора m1 в памяти
В языках, где память распределяется до выполнения программы на этапе компиляции (C, PASCAL, FORTRAN), при описании типа вектора граничные значения индексов должны быть определены. В языках, где память может распределяться динамически (ALGOL, PL/1), значения индексов могут быть заданы во время выполнения программы. Количество байт непрерывной области памяти, занятых одновременно вектором, определяется по формуле: ByteSise = ( k - n + 1 ) * Sizeof (тип) Обращение к i-му элементу вектора выполняется по адресу вектора плюс смещение к данному элементу. Смещение i-го элемента вектора определяется по формуле: ByteNumer = ( i- n ) * Sizeof (тип), а адрес его: @ ByteNumber = @ имя + ByteNumber. где @ имя - адрес первого элемента вектора. Например: var МAS: array [ 5..10 ] of word. Базовый тип элемента вектора - Word требует 2 байта, поэтому на каждый элемент вектора выделяется по два байта. Тогда табл. 3.1 смещений элементов вектора относительно @Mas выглядит так:
Таблица 3.1
Этот вектор будет занимать в памяти: (10-5+1)*2 = 12 байт. Смещение к элементу вектора с номером 8: (8-5)*2 = 6 Адрес элемента с номером 8: @ MAS + 6. При доступе к вектору задается имя вектора и номер элемента вектора. Таким образом, адрес i-го элемента может быть вычислен как: @Имя[i] = @Имя + i*Sizeof(тип) - n*Sizeof(тип) (3.1) Это вычисление не может быть выполнено на этапе компиляции, так как значение переменной i в это время еще неизвестно. Следовательно, вычисление адреса элемента должно производиться на этапе выполнения программы при каждом обращении к элементу вектора. Но для этого на этапе выполнения, во-первых, должны быть известны параметры формулы (3.1): @Имя Sizeof(тип), n, а во-вторых, при каждом обращении должны выполняться две операции умножения и две - сложения. Преобразовав формулу (3.1) в формулу (3.2), получим: @Имя[i] = A0 + i*Sizeof(тип)щ (3.2) A0 = @Имя - n*Sizeof(тип) ы Таким образом сокращается число хранимых параметров до двух, а число операций - до одного умножения и одного сложения, так как значение A0 может быть вычислено на этапе компиляции и сохранено вместе с Sizeof(тип) в дескрипторе вектора. Обычно в дескрипторе вектора сохраняются и граничные значения индексов. При каждом обращении к элементу вектора заданное значение сравнивается с граничными и программа аварийно завершается, если заданный индекс выходит за допустимые пределы. Таким образом, информация, содержащаяся в дескрипторе вектора, позволяет, во-первых, сократить время доступа, а, во-вторых, обеспечивает проверку правильности обращения. Но за эти преимущества приходится платить, во-первых, быстродействием, так как обращения к дескриптору - это команды, во-вторых, памятью как для размещения самого дескриптора, так и для команд, с ним работающих. Можно ли обойтись без дескриптора вектора? В языке C, например, дескриптор вектора отсутствует, точнее, не сохраняется на этапе выполнения. Индексация массивов в C обязательно начинается с нуля. Компилятор каждое обращение к элементу массива заменяет на последовательность команд, реализующую частный случай формулы (3.1) при n = 0: @Имя[i] = @Имя + i*Sizeof(тип) Программисты, привыкшие работать на C, часто вместо выражения вида: Имя[i] употребляют выражение вида: *(Имя+i). Но, во-первых, ограничение в выборе начального индекса само по себе может являться неудобством для программиста, во-вторых, отсутствие граничных значений индексов делает невозможным контроль выхода за пределы массива. Программисты, работающие с C, хорошо знают, что именно такие ошибки часто являются причиной "зависания" C-программы при ее отладке.
Массивы Логическая структура Массив - такая структура данных, которая характеризуется: - фиксированным набором элементов одного и того же типа; - каждый элемент имеет уникальный набор значений индексов; - количество индексов определяет мерность массива, например, два индекса - двумерный массив, три индекса - трехмерный массив, один индекс - одномерный массив или вектор; - обращение к элементу массива выполняется по имени массива и значениям индексов для данного элемента. Другое определение: массив - это вектор, каждый элемент которого - вектор. Синтаксис описания массива представляется в виде: <Имя> : Array [n1..k1] [n2..k2] .. [nn..kn] of <Тип>. Для случая двумерного массива: Mas2D : Array [n1..k1] [n2..k2] of <Тип>, или Mas2D : Array [n1..k1 , n2..k2] of <Тип> Наглядно двумерный массив можно представить в виде таблицы из (k1-n1+1) строк и (k2-n2+1) столбцов. Физическая структура Физическая структура - это размещение элементов массива в памяти ЭВМ. Для случая двумерного массива, состоящего из (k1-n1+1) строк и (k2-n2+1) столбцов, физическая структура представлена на рис. 3.3.
Рис. 3.3. Физическая структура двумерного массива из (k1-n1+1) строк и (k2-n2+1) столбцов
Многомерные массивы хранятся в непрерывной области памяти. Размер слота определяется базовым типом элемента массива. Количество элементов массива и размер слота определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так, в FORTRAN элементы распределяются по столбцам - так, что быстрее меняются левые индексы, в PASCAL - по строкам - изменение индексов выполняется в направлении справа налево. Количество байтов памяти, занятых двумерным массивом, определяется по формуле : ByteSize = (k1-n1+1)*(k2-n2+1)*SizeOf(Тип) (3.3)
Адресом массива является адрес первого байта начального компонента массива. Смещение к элементу массива Mas[i1,i2] определяется по формуле: ByteNumber = [(i1-n1)*(k2-n2+1)+(i2-n2)]*SizeOf(Тип) (3.4) его адрес : @ByteNumber = @mas + ByteNumber. Например: var Mas : Array [3..5] [7..8] of Word; Базовый тип элемента Word требует два байта памяти, тогда табл. 3.2 смещений элементов массива относительно @Mas будет выглядеть так:
Таблица 3.2
Этот массив будет занимать в памяти: (5-3+1)*(8-7+1)*2=12 байт; а адрес элемента Mas[4,8]: @Mas+((4-3)*(8-7+1)+(8-7)*2 = @Mas+6
Операции Важнейшая операция физического уровня над массивом - доступ к заданному элементу. Как только реализован доступ к элементу, над ним может быть выполнена любая операция, имеющая смысл для того типа данных, которому соответствует элемент. Преобразование логической структуры в физическую, в ходе которого многомерная логическая структура массива преобразуется в одномерную физическую структуру, называется процессом линеаризации. В соответствии с формулами (3.3), (3.4) и по аналогии с вектором (3.1), (3.2) для двумерного массива с границами изменения индексов: [B(1)..E(1)][B(2)..E(2)], размещенного в памяти по строкам, адрес элемента с индексами [I(1),I(2)] может быть вычислен как:
Addr[I(1),I(2)] = Addr[B(1),B(2)]++{[I(1)-B(1)]*[E(2)-B(2)+1]+[I(2)-B(2)]}*SizeOf(Тип) (3.5)
Обобщая (3.5) для массива произвольной размерности:
Mas[B(1)..E(2)][B(2)..E(2)]...[B(n)..E(n)] , получим где D(m) зависит от способа размещения массива. При размещении по строкам: D(m)=[E(m+1)-B(m+1)+1]*D(m+1), где m = n-1,...,1 и D(n)=1, при размещении по столбцам: D(m)=[E(m-1)-B(m-1)+1]*D(m-1), где m = 2,...,n и D(1)=1. При вычислении адреса элемента наиболее сложным является вычисление третьей составляющей формулы (3.6), т.к. первые две не зависят от индексов и могут быть вычислены заранее. Для ускорения вычислений множители D(m) также могут быть вычислены заранее и сохраняться в дескрипторе массива. Дескриптор массива, таким образом, содержит: · начальный адрес массива - Addr[I(1),I(2),...,I(n)]; · число измерений в массиве - n; · постоянную составляющую формулы линеаризации (первые две составляющие формулы (3.6); · для каждого из n измерений массива: · значения граничных индексов - B(i), E(i); · множитель формулы линеаризации - D(i). Одно из определений массива гласит, что это вектор, каждый элемент которого - вектор. Некоторые языки программирования позволяют выделить из многомерного массива одно или несколько измерений и рассматривать их как массив меньшей мерности. Например: если в PL/1 - программе объявлен двумерный массив: DECLARE A(10,10) BINARY FIXED; то выражение A[*,I] - будет обращаться к одномерному массиву, состоящему из элементов: A(1,I), A(2,I),...,A(10,I). Символ-джокер "*" означает, что выбираются все элементы массива по тому измерению, которому соответствует заданный джокером индекс. Использование джокера позволяет также задавать групповые операции над всеми элементами массива или над выбранным его измерением, например: A(*,I) = A(*,I) + 1. К операциям логического уровня над массивами необходимо отнести такие, как сортировка массива, поиск элемента по ключу. Наиболее распространенные алгоритмы поиска и сортировок будут рассмотрены в данной главе ниже.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

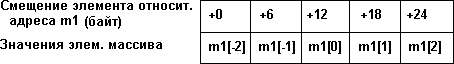


 , (3.6)
, (3.6)