
|
|
Теоретическая кривая распределения
Если постепенно увеличивать размер партии, то эмпирическая кривая распределения будет приближаться по форме к холмообразной кривой, представленной пунктирной линией на рис 13.1, а частота
Закон нормального распределения В математической статистике доказано и подтверждено многочисленными экспериментами, что для многих случайных процессов теоретическая частость определяется следующим выражением
В нем
называется плотностью распределения случайной величины по нормальному закону или плотностью нормального распределения. Запись Плотность распределения следует рассматривать, как вероятность появления случайной величины Чтобы определить вероятность появления случайной величины
Это выражение называется интегралом вероятности. В геометрическом смысле этот интеграл представляет собой площадь под кривой нормального распределения в пределах заданного интервала. Для достаточно узкого интервала согласно теореме о среднем
Кривая нормального распределения имеет следующие свойства: 1. Ось 2. При
3. Кривая имеет две точки перегиба
4. Если случайная величина может принимать любые численные значения в интервале
Это свойство вытекает из положения, что вероятность появления случайной величины на бесконечно большом интервале равна единице. Положение кривой относительно начала координат, и ее форма определяются двумя параметрами Нормирование распределения
Введем новую переменную
Соответственно для интеграла вероятности (13.14) будем иметь
где Это действие называется нормированиемраспределения случайных величин. Сущность операции нормирования заключается к приведению множества кривых распределения к одной, зависящей только от нормированной переменной. Для этой кривой среднее арифметическое значение равно нулю, а среднее квадратическое отклонение равно единице. Графическая интерпретация процедуры нормирования заключается в совмещении центра группирования с началом новой системы координат
Функция Лапласа
Применение функции Лапласа позволяет вычислить теоретические частость и частоту. Примем в формуле (13.20)
Интеграл Геометрически функцией Лапласа определяется площадь фигуры под кривой нормированного нормального распределения в промежутке от 0 до Выразим теоретическую частость через функции Лапласа. Из выражений (13.13) получаем
Выполним операцию нормирования. В результате замены переменной будем иметь
Пусть
где Тогда

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и частность
и частность  на каждом интервале будут стремиться к некоторым значениям
на каждом интервале будут стремиться к некоторым значениям  и
и 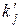 на данном интервале, которые называются теоретической частотой и теоретической частостью. Очевидно, что в пределе при
на данном интервале, которые называются теоретической частотой и теоретической частостью. Очевидно, что в пределе при 
 ;
;  , а дискретная случайная величина
, а дискретная случайная величина  становится непрерывной случайной величиной
становится непрерывной случайной величиной  . График зависимости
. График зависимости  или
или  от
от  . (13.13)
. (13.13)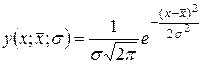
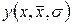 означает, что плотность является функцией от непрерывной случайной величины
означает, что плотность является функцией от непрерывной случайной величины  - среднего арифметического значения и
- среднего арифметического значения и 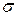 - среднего квадратического отклонения. График этой функции приведен на рис. 13.2 и называется кривой нормального распределения.
- среднего квадратического отклонения. График этой функции приведен на рис. 13.2 и называется кривой нормального распределения. в точкахобласти ее определения. Там где
в точкахобласти ее определения. Там где  , вероятность появления случайной величины максимальная. С увеличением разности
, вероятность появления случайной величины максимальная. С увеличением разности  эта вероятность уменьшается. В этой связи функцию
эта вероятность уменьшается. В этой связи функцию 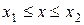 с плотностью распределения по нормальному закону, необходимо вычислить интеграл
с плотностью распределения по нормальному закону, необходимо вычислить интеграл ,
,  . (13.14)
. (13.14) ;
; 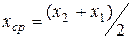 . (13.15)
. (13.15) является асимптотой для ее ветвей.
является асимптотой для ее ветвей.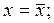
 . (13.16)
. (13.16) и
и  , которые находятся на расстоянии
, которые находятся на расстоянии  . (13.17)
. (13.17) , то независимо от
, то независимо от  и
и 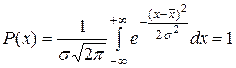 . (13.18)
. (13.18)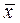 и
и 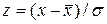 . После замены переменной в (13.13) для плотности вероятности получаем
. После замены переменной в (13.13) для плотности вероятности получаем (13.19)
(13.19) (13.20)
(13.20) и
и  - новые пределы интегрирования.
- новые пределы интегрирования.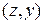 . В этом случае кривая нормированного нормального распределения становится симметричной относительно оси ординат, а функция
. В этом случае кривая нормированного нормального распределения становится симметричной относительно оси ординат, а функция  называется плотностью нормированного распределения.
называется плотностью нормированного распределения. ;
;  . Тогда
. Тогда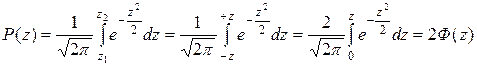 , (13.21)
, (13.21)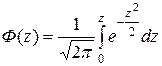 называется функцией Лапласа.
называется функцией Лапласа. . Интеграл в
. Интеграл в 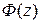 нельзя выразить в элементарных функциях и его значение задано в специальных таблицах.
нельзя выразить в элементарных функциях и его значение задано в специальных таблицах. . (13.22)
. (13.22) .
. <
<  . Тогда, выражая
. Тогда, выражая  через функции Лапласа, получим
через функции Лапласа, получим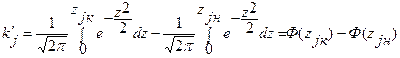 , (13.23)
, (13.23) и
и  - новые пределы интегрирования.
- новые пределы интегрирования. (13.24)
(13.24)