|
|
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза?
Задание B11 (№ 27095) Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
Задание B11 (№ 27096) Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Задание B11 (№ 27097) Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Задание B11 (№ 27098) Диагональ куба равна
Задание B11 (№ 27099) Объем куба равен
Задание B11 (№ 27100) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Задание B11 (№ 27101) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Задание B11 (№ 27102) Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Задание B11 (№ 27103) Диагональ прямоугольного параллелепипеда равна
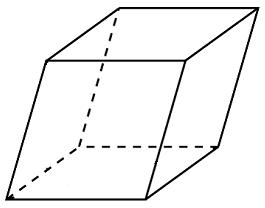
Задание B11 (№ 27104) Гранью параллелепипеда является ромб со стороной 1 и острым углом 60
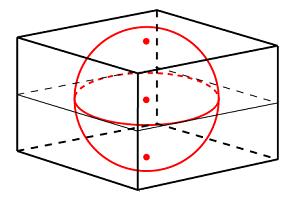
Задание B11 (№ 27105) Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
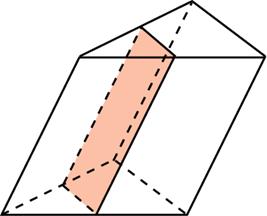
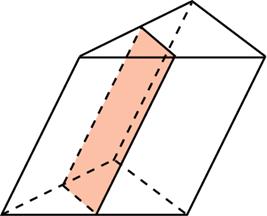
Задание B11 (№ 27106) Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Задание B11 (№ 27107) Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Задание B11 (№ 27108) Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны
Задание B11 (№ 27109) В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Задание B11 (№ 27110) Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60
Задание B11 (№ 27111) Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Задание B11 (№ 27112) От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части. Задание B11 (№ 27113) Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
Задание B11 (№ 27114) Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
Задание B11 (№ 27115) От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
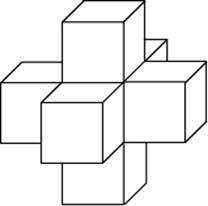
Задание B11 (№ 27116) Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. Задание B11 (№ 27117) Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Задание B11 (№ 27118) Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Задание B11 (№ 27120) Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
Задание B11 (№ 27121) Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на
Задание B11 (№ 27122) Конус получается при вращении равнобедренного прямоугольного треугольника
Задание B11 (№ 27123) Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Задание B11 (№ 27124) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

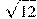 . Найдите его объем.
. Найдите его объем.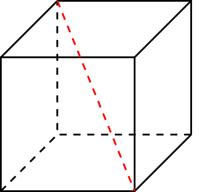
 . Найдите его диагональ.
. Найдите его диагональ.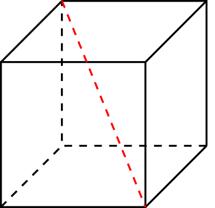


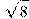 и образует углы 30
и образует углы 30 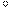 , 30
, 30 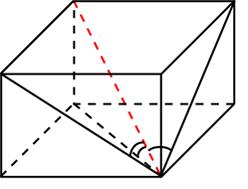
 и наклонены к плоскости основания под углом 30
и наклонены к плоскости основания под углом 30 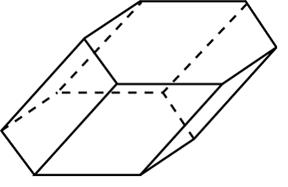


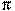 .
.
 вокруг катета, равного 6. Найдите его объем, деленный на
вокруг катета, равного 6. Найдите его объем, деленный на