
|
|
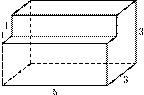
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.Задание B11 (№ 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25561) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25581) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25601) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25621) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25641) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25661) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25681) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25701) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25721) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 25881) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание B11 (№ 27041) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Задание B11 (№ 27042) Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Задание B11 (№ 27043) Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
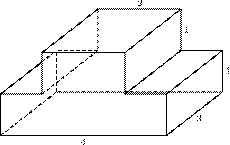
Задание B11 (№ 27044) Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Задание B11 (№ 27045) В цилиндрический сосуд налили
Задание B11 (№ 27046) В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Задание B11 (№ 27047) В сосуд, имеющий форму правильной треугольной призмы, налили 2300
Задание B11 (№ 27048) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает
Задание B11 (№ 27049) В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
Задание B11 (№ 27050) В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны
Задание B11 (№ 27051) Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
Задание B11 (№ 27052) Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Задание B11 (№ 27053) Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах. Задание B11 (№ 27054) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Задание B11 (№ 27055) Площадь поверхности куба равна 18. Найдите его диагональ.
Задание B11 (№ 27056) Объем куба равен 8. Найдите площадь его поверхности.
Задание B11 (№ 27057) Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Задание B11 (№ 27058) Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на
Задание B11 (№ 27059) Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Задание B11 (№ 27060) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|













 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в  .
.

 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в
см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в  раза больше, чем у первого? Ответ выразите в см.
раза больше, чем у первого? Ответ выразите в см. . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы.
 . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы.





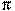 .
.
