
|
|
Уравнения переходного процесса и их особенности
Эти уравнения формулируются по 2-му закону Кирхгофа и имеют вид: для потокосцеплений –

для обмоток машины
где k – индекс фазы, k =А, В, С; f, 1d, 1f –индексы обмотки возбуждения и демпферных обмоток соответственно. Считают напряжения известными, а токи – неизвестными. Система уравнений (3.1) – линейная с периодическими коэффициентами L и M. Периодичность последних обусловлена изменением магнитных свойств среды вследствие вращения ротора. Число различных М в два раза меньше, чем использовано в системе, т.к. согласно принципу взаимности В настоящее время отсутствуют методы аналитического решения системы дифференциальных уравнений такого рода. Поэтому основным подходом к решению инженерных задач, связанных с исследованием переходных процессов во вращающихся электрических машинах, следует считать применение численных методов интегрирования систем обыкновенных дифференциальных уравнений. Такой подход требует использования ЭВМ и имеет преимущества в точности и простоте расчётов, но не даёт физических оценок процессам. Этот недостаток устраняется использованием аналитических решений, которые возможны только для дифференциальных уравнений с постоянными коэффициентами. Особенность приведённой системы – периодичность коэффициентов, обусловленная вращением ротора, устраняется, если систему уравнений записать в системе координат, жестко связанной с ротором. В качестве последней удобно выбирать оси симметрии ротора. Переход от системы координат А, В, С к системе d, q, o осуществляется следующим образом:
где
Для фазы А в системе, жестко связанной с ротором, уравнения будут иметь вид:
Последнее уравнение выражает второй закон Кирхгофа и должно выполняться в любой момент времени, т.е. при любом Уравнение вида
Потокосцепление статора в продольной оси имеет две составляющие:
Первое слагаемое – потокосцепление самоиндукции, второе – потокосцепление взаимоиндукции между статором и ротором в продольной оси (в системе относительных единиц x=L). Для машин без демпферных обмоток уравнения имеют вид: для потокосцеплений –
для обмотки возбуждения –
Для машин с демпферными обмотками система уравнений дополняется уравнениями
Для потокосцеплений уравнения имеют вид:
где
Приведённые выше уравнения носят название уравнений Парка-Горева и составляют основу теории двух реакций, известной в курсе "Электрические машины". В уравнениях баланса напряжений в обмотках статора составляющие имеют достаточно простой физический смысл. Первое слагаемое (производная от потокосцепления) можно рассматривать как ЭДС, связанную с изменением потокосцепления (трансформаторная ЭДС); второе слагаемое – как ЭДС, обусловленную вращением обмоток статора относительно магнитного потока ротора (в системе координат, жёстко связанной с ротором). Уравнения Парка-Горева характеризуются как линейные, с постоянными коэффициентами, не зависящими от положения ротора. Поэтому для них возможны аналитические решения с последующим количественным и качественным анализом. Наиболее удобным методом решения уравнений Парка-Горева является операторный метод, основанный на преобразованиях Лапласа, которые позволяют заменить операции интегрирования и дифференцирования на алгебраические. Структура операторных уравнений полностью совпадает с исходными дифференциальными уравнениями, если начальный запас энергии в машине был равен нулю. Согласно принятым допущениям о линейности объекта можно использовать принцип наложения, т.е. рассматривать переходный процесс с нулевыми начальными условиями как сумму процессов: стационарного, определяющего ненулевые начальные условия, и собственно переходного, развивающегося с нулевых начальных условий. Для машины с демпферными обмотками последний можно характеризовать операторными уравнениями Парка-Горева:
При записи этих уравнений принять Рассмотрение практических задач на основе приведённых уравнений требует предварительного решения ряда вопросов, имеющих и самостоятельное значение. Это прежде всего оценка величины

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 –
–
 и т.д.
и т.д.

 – параметр режима в фазных координатах;
– параметр режима в фазных координатах; – угол между осью координат и осью симметрии.
– угол между осью координат и осью симметрии.
 при любом
при любом  т.е.
т.е.
 .
.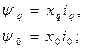



 – реактивное сопротивление обмоток статора соответственно в продольной и поперечной осях симметрии;
– реактивное сопротивление обмоток статора соответственно в продольной и поперечной осях симметрии; – реактивное сопротивление демпферных обмоток ротора, расположенных соответственно в продольной и поперечной осях симметрии;
– реактивное сопротивление демпферных обмоток ротора, расположенных соответственно в продольной и поперечной осях симметрии; – реактивное сопротивление взаимной индукции обмоток статора и ротора, расположенных соответственно в продольной и поперечной осях;
– реактивное сопротивление взаимной индукции обмоток статора и ротора, расположенных соответственно в продольной и поперечной осях;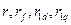 – активное сопротивление обмоток статора, возбуждения демпферных обмоток в продольной и поперечной осях соответственно;
– активное сопротивление обмоток статора, возбуждения демпферных обмоток в продольной и поперечной осях соответственно; – реактивное сопротивление обмотки возбуждения.
– реактивное сопротивление обмотки возбуждения. (3.2)
(3.2)
 (в относительных единицах
(в относительных единицах  ). Символ
). Символ  означает, что соответствующие параметры режима отвечают только нулевым начальным условиям.
означает, что соответствующие параметры режима отвечают только нулевым начальным условиям.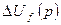 и построение динамических характеристик машины.
и построение динамических характеристик машины.