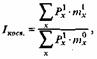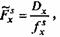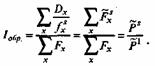СТАНДАРТИЗАЦИЯ КОЭФФИЦИЕНТОВ СМЕРТНОСТИ

Величина общих коэффициентов смертности, будучи свободной от влияния абсолютной численности населения, тем не менее зависит от структурных факторов, т.е. от соотношения численностей мужского и женского населения, городского и сельского населения, состоящих и не состоящих в браке и т.д. Одним из наиболее сильных факторов, оказывающих влияние на величину общих коэффициентов, является возрастная структура населения. Сказанное здесь касается общих коэффициентов и для других демографических процессов.

Влияние структурных факторов на величину общих коэффициентов можно проиллюстрировать следующим гипотетическим примером, в котором рассматриваются три страны с одинаковыми по численности, но имеющими разную возрастную структуру населениями (табл. 6.3)².

В странах А и В - одинаковые повозрастные коэффициенты смертности. Однако в стране А общий коэффициент смертности в полтора с лишним раза больше, чем в стране В. Это является прямым результатом того, что страна А имеет более высокую долю детей в возрасте 0-4 года. Для этой группы свойственны повышенные значения повозрастных показателей смертности (особенно в группе 0 лет).

С другой стороны, страны В и С имеют одинаковые величины общих коэффициентов смертности, но существенно разные повозрастные коэффициенты. В стране С гораздо выше доля населения в старших возрастах (где можно было бы ожидать более высоких показателей смертности). Однако в этой стране показатель повозрастной смертности для старших возрастов в два раза меньше, чем в странах А и В. Благодаря этому страна С, хотя в ней более старое население, имеет общий коэффициент смертности такой же, как и страна В.

Ясно, что напрямую сопоставлять данные об общих коэффициентах смертности в этих условных странах невозможно. И в целом действие структурных факторов является одной из причин, делающих практически несопоставимыми данные о демографических показателях разных территорий или различных периодов (если по прошествии времени произошли значительные изменения различных структур населения).

Поэтому приходится использовать различные методы, позволяющие устранить искажающее влияние структурных факторов, прежде всего возрастной структуры. Одним из таких

Таблица 6,3

Влияние возрастной структуры на величину общих коэффициентов смертности

методов является использование специальных и частных коэффициентов, на которые структурные факторы не влияют или влияют гораздо в меньшей степени.

Еще одним способом устранения влияния структурных факторов и является стандартизация демографических коэффициентов. Метод стандартизации был предложен и впервые применен в анализе смертности английским статистиком и демографом У. Фарром (W. Farr, 1807-1883).

Применение стандартизации основано как раз па разложении общих коэффициентов на сомножители, выражающие, с одной стороны, интенсивность демографического процесса, а с другой, численность или долю соответствующего субнаселения во всем населении.

Общие коэффициенты суть взвешенные суммы частных или специальных. При этом частные или специальные коэффициенты характеризуют интенсивность процесса (или, что то же самое, соответствующее среднее поведение), а веса, которыми являются численности или доли соответствующих субнаселений, характеризуют структурный фактор.

Суть стандартизации заключается в том, что реальные общие коэффициенты сравниваются с показателями некоторого условного населения, которое получается, если проделать следующее.

Интенсивность демографического процесса в некотором населении (реальном или искусственно сконструированном) или его структура принимается за стандарт*. Затем для каждого из сравниваемых населений рассчитывается стандартизованный общий коэффициент, который показывает, какими были бы общие коэффициенты рассматриваемого процесса в данном населении, если бы интенсивность этого процесса в нем или его структура были бы такими же, как и в населении стандарта. При этом, в зависимости от того, что именно принимается за стандарт (интенсивность или структура), применяют различные методы стандартизации.

Наибольшее распространение имеют прямая стандартизация, косвенная и обратная, к рассмотрению которых мы и переходим. Покажем суть этих методов на примере стандартизации общих коэффициентов смертности.

Методы стандартизации

При прямой стандартизации** повозрастные коэффициенты смертности реального населения перевзвешиваются по возрастной структуре стандарта. Таким образом получается то число смертей, которое имело бы место в реальном населении, если бы его возрастная структура была такой же, как и возрастная структура стандарта. Разделив это число на число смертей в стандартном населении, получают индекс прямой стандартизации. Если общий коэффициент смертности стандарта умножить на этот индекс, то получим стандартизованный общий коэффициент смертности, который показывает, какова была бы величина общего коэффициента смертности в реальном населении, если бы его возрастная структура была такой же, как и возрастная структура стандарта.

Отсюда CMR_cmаm = CMR₀-I_пр , где CMR_cman - стандартизованный общий коэффициент смертности; CMR₀ - общий коэффициент смертности стандарта.

Прямую стандартизацию можно применять, если известны повозрастные коэффициенты смертности сравниваемых реальных населений и возрастная структура стандарта. При этом за стандартную возрастную структуру можно принять либо возрастную структуру какого-либо реального населения, либо искусственно сконструированную.

При прямой стандартизации существует опасность, что и индекс стандартизации и стандартизованный коэффициент окажутся под влиянием повозрастного коэффициента, вес которого мал в реальном населении и, напротив, велик в населении стандартном. Избежать этой опасности позволяет косвенная стандартизация.

В случае косвенной стандартизации* поступают прямо противоположным образом: повозрастные коэффициенты смертности стандарта перевзвешиваются по возрастной структуре реального населения. Таким образом получается то число смертей, которое бы имело место в реальном населении, если бы его возрастная смертность была такой же, как и повозрастная смертность стандартного населения. Разделив число смертей в реальном населении на их ожидаемое число, получают индекс косвенной стандартизации. Если общий коэффициент смертности стандарта умножить на этот индекс, то получим стандартизованный общий коэффициент смертности, который показывает, какова была бы величина общего коэффициента смертности в реальном населении, если бы повозрастные коэффициенты смертности в нем были такими же, как и в населении стандарта.

Все сказанное можно выразить в виде следующей формулы:

где 1_косв - индекс косвенной стандартизации; P_х¹ - возрастная структура реального населения, выраженная в абсолютных величинах или долях; т_х⁰ - повозрастные коэффициенты смертности в стандартном населении и т_х¹ - повозрастные коэффициенты смертности в данном населении.

Отсюда CMR_cman - CMR₀ - 1_косв, где CMR_cman - стандартизованный общий коэффициент смертности; CMR₀ - общий коэффициент стандарта смертности.

Косвенную стандартизацию целесообразно применять, если известны возрастные структуры реального населения и стандарта и повозрастные интенсивности демографических процессов в стандартном населении.

Косвенная стандартизация имеет широкое применение при анализе смертности, для которого она, собственно, и была разработана. Однако в последние полвека метод косвенной стандартизации активно применяется и в изучении рождаемости. Сфера его применения здесь - это анализ сравнительной роли демографической структуры (возрастной, брачной и др.) и поведения индивидов в формировании уровня рождаемости, о чем шла речь в предыдущей главе. В частности, именно косвенная стандартизация лежит в основе индексов рождаемости Э. Коула и модели т.н. гипотетического минимума естественной рождаемости В.А. Борисова.

Метод обратной стандартизации* , иначе называемый методом ожидаемой численности населения, применяется в том случае, когда отсутствуют данные о возрастной структуре данного населения, но зато есть данные об его общей численности и о числе демографических событий в нем (случай нередкий во многих развивающихся странах, где переписи населения стали проводиться лишь недавно). А также, разумеется, известны повозрастные коэффициенты смертности стандарта. Зная это, можно восстановить условную среднюю численность всех возрастных групп реального населения при условии, что реальное население имеет те же повозрастные коэффициенты смертности, что и население стандарта. Для этого надо просто поделить известное число смертей на стандартный повозрастный коэффициент смертности:

где f_x^s - условная численность группы в возрасте х лет; D_x - реальное число смертей и f_x^s - повозрастные коэффициенты смертности стандарта. Тогда, просуммировав все F_x^s , можно восстановить ту общую численность населения, которая должна была бы быть, если бы реальное население имело те же повозрастные коэффициенты смертности, что и население стандарта. И затем, поделив эту условную численность на реальную, получим индекс обратной стандартизации:

В знаменателе этого выражения стоит реальная средняя численность населения, в числителе - его гипотетическая («ожидаемая») численность, которая при стандартных повозрастных интенсивностях смертности продуцировала бы в каждом возрасте фактическое число смертей.

Умножив индекс обратной стандартизации на общий коэффициент стандарта смертности, получим стандартизованный общий коэффициент смертности, то значение общего коэффициента смертности для реального населения, которое бы имело место, если бы его повозрастные коэффициенты смертности были такими же, что и в населении стандарта.

Завершая данный параграф, необходимо подчеркнуть следующее. Используя стандартизованные коэффициенты смертности, надо помнить, что они не имеют самостоятельного значения, поскольку зависят от выбранного стандарта. Поэтому сфера их применения ограничивается лишь сравнением различных населений друг с другом и то при условии, что стандартизация проведена одним и тем же методом и с использованием одного и того же стандарта. При этом в качестве стандарта необходимо выбирать население (реальное или искусственно сконструированное), демографическая структура которого (возрастная прежде всего) близка к возрастным структурам сравниваемых населений, хотя и отличается от них.

ТАБЛИЦЫ СМЕРТНОСТИ

Таблицы смертности (дожития) - это первый и, пожалуй, самый распространенный и важный вид демографических таблиц. Как уже говорилось, именно с разработкой Дж. Граунтом первой в мире таблицы смертности связывают возникновение демографии как науки.

Принимая во внимание, что мы установили, что из каждых 100 родившихся приблизительно 36 не доживают до шестилетнего возраста и что, возможно, один доживает до 76 лет, мы, имея 7 десятилетий между 6 и 76 годами, пытались найти 6 промежуточных пропорциональных чисел между 64, доживающими до 6 лет, и тем 1, который доживает до76 лет. Мы нашли, что нижеследующие числа достаточно близки к истине: из каждых 100 родившихся умирают в пределах первых 6 лет - 36. В течение следующих 10 лет, или второго десятилетия, - 24. В течение третьего десятилетия - 15. В течение четвертого десятилетия - б. В течение пятого десятилетия - 4. В течение шестого - 3. В течение седьмого - 2. И в течение восьмого - 1.

Отсюда следует, что из упомянутых 100 родившихся в 6 лет остаются в живых 64. В 16 лет - 40; в 26 - 25; в 36 - 16; в 46 - 10; в 56 - 6; в 66 - 3; в

Граунт Дж. Естественные и политические наблюдения, сделанные над бюллетенями смертности.... Лондон, 1662. Цит. по: Smith D.P. Formal Demography. N. Y., London. 1983. P. 73.

Таблицы смертности (дожития) - это числовые модели смертности, служащие для характеристики ее общего уровня и возрастных особенностей в различных населениях. Они представляют собой систему упорядоченных по возрасту и взаимосвязанных между собой рядов чисел, которые в своей совокупности описывают процесс вымирания некоторого теоретического поколения с фиксированной начальной численностью (корень таблицы). Обычно ее принимают равной некоторой степени 10, т.е.10 000, 100 000, 1 000 000 и т.п. Чаше всего за корень таблицы смертности принимают 100 000.

В демографии различают таблицы смертности для реального и условного поколения.

В зависимости от шага временной шкалы различают полные (шаг = 1 году) и краткие (шаг = 5 или 10 годам) таблицы.

Показатели (функции) таблиц смертности делятся на интервальные и кумулятивные. Первые характеризуют смертность на данном интервале возраста, вторые - за весь период жизни до или после данного точноговозраста.

Показатели (функции) таблиц смертности связаны между собой определенными соотношениями. Все они могут быть вычислены почти из любого из них, но обычно за исходный принимается тот, который наиболее простым и ясным образом характеризует процесс смертности и легче всего получается из статистических данных о смертности. Таким показателем является интервальная вероятность умереть в возрасте (х, х+п) лет, наиболее естественным образом связанная с повозрастными коэффициентами смертности. Обычно построение таблиц смертности начинается именно с этого показателя. И всю историю развития методов такого построения можно рассматривать как совершенствование методов перехода от повозрастных коэффициентов смертности к табличным интервальным вероятностям смерти в возрасте (х, х + п) лет.

Рассмотрим на примере полной таблицы смертности основные ее функции (табл. 6.4):

Графа 1.Возрастной интервал (х, х + 1) год.

Графа 2. Числа доживающих до точного возраста х лет (l_Х). Первое число в этой графе - это конвенциональный корень таблицы смертности. Все прочие представляют собой числа доживающих до точного возраста х лет и равны разности чисел доживающих до точного возраста х-1 год и чисел умирающих на интервале возраста (х, х + 1) лет, т.е. l_x = l_{x 1 -} d_x. С другой стороны, поскольку d_x = l_x*q_x, каждое l_x=l_{x 1} - l_{x 1}* *q_{x 1} = l_{x 1}*(1 - q_{x 1})= l_x *₁P_{x 1}. И поэтому l_x = l₀*p₀*p₁*...*p_{x 1}. Иначе говоря, числа доживающих равны вероятности того, что каждая единица исходной совокупности 1₀ доживет до точного возраста х лет.

Графа 3. Вероятность умереть на интервале возраста (х, х + 1) год, q_x. Каждое q_x представляет собой вероятность того, что человек, достигший точного возраста х лет, не доживет до возраста х + 1 год. Эти вероятности рассчитываются на основе соответствующих повозрастных коэффициентов смертности реального населения. Именно их этих вероятностей затем рассчитываются все остальные показатели таблиц смертности.

Графа 4. Вероятность остаться в живых на интервале возраста (х, х+1) год,р_х. Каждое p_x представляет собой вероятность того, что человек, достигший точного возраста х лет, доживет и до возраста х + 1 год. Является дополнением вероятности q_x до 1,т.е.р_х = 1 - q_x.

Графа 5. Числа умирающих на интервале возраста (х, х + 1) год, d_x. Эти числа также зависят от корня таблицы. Числа в графах 3-5 рассчитываются из наблюдаемых q_x корня таблицы с использованием следующих соотношений: d_x= l_xq_x; l_x+l = l_x - d_x и р_x = 1-q_x.

Графа 6. Доля последнего года жизни для умирающих на интервале возраста (х, х+1) лет, а'_х. Каждый из d_x, умирающих на возрастном интервале (х, х+1) лет, прожил полные х лет плюс некоторую часть этого возрастного интервала. Средняя из этих долей и обозначается а '_х. Ее величина зависит от характера распределения случаев смерти внутри возрастного интервала (х, х + \) лет. В самых младших возрастах это распределение имеет I левостороннюю асимметрию (т.е. сдвинуто к началу возрастного интервала), и потому величина а '_х меньше 1/2, чему она была бы равна в случае равномерного распределения и чему она конвенционально равна для возрастов старше 4 лет. Данный показатель играет важную роль в современных модификациях т.н. демографического метода построения таблиц смертности.

Доля последнего года жизни для умирающих на интервале возраста (х, х + п) лет, (а '_х) рассчитывается в зависимости от особенностей распределения смертности на данном возрастном интервале. В таблице приведены значения этого параметра, взятые из работы американского демографа Чин Лонг Чаня (См.: Chin Long Chiang. The Life Table and Its Construction // Introduction to Stochastic Processes in Biostatistics. N.Y., 1968. PP. 189-214).

Графа 7. Число человеко-лет, прожитых в возрастном интервале (х, х + 1) лет. L_x. Каждый из тех, кто проживет полный

Таблица 6,4

Функции таблиц смертности

возрастной интервал (х, х + 1) лет, вносит в общее число человеко-лет (/_r- d_x) лет. Каждый же из тех, кто умрет на этом интервале возраста, вносит в L_x в среднем а '_х часть этого интервала. Отсюда: L_x - (l_x-d_x)'+ а'_х- d_x (х = О,1, 2- 1). В полных таблицах смертности в возрастах 5 лет и старше величина а '_х принимается равной 1/2 и, поэтому, для этих возрастов L_x - полными аналогами среднегодового населения.

Графа 8.Число человеко-лет, которое предстоит прожить после достижения точного возраста х лет, Т_x Это число равно сумме человеко-лет, прожитых в каждом возрастном интервале начиная с возраста х лет, или Т_х = L_x.

Графа 9.Средняя ожидаемая продолжительность предстоящей жизни в возрасте х лет, е^л_х. Это число показывает, сколько в среднем предстоит прожить человеку, достигшему возраста х лет. Поскольку всем дожившим до этого возраста (их число равно l_x предстоит прожить Т_х лет, постольку е^л_х=T_x/l_x , лет.

Каждое е^л_х суммирует смертность в возрастах старше x лет, что делает эту графу наиболее важной в таблице смертности. Более того, это одна из трех функций таблицы смертности (наряду с q_x и а'_х), которая имеет смысл безотносительно к корню таблицы. Как правило, е^л_х убывает с возрастом. Единственное исключение представляет собой возраст 0 лет, когда е^л₀< e^л₁ из-за высокой младенческой смертности. Это называется парадоксом младенческой смертности. В высокоразвитых странах с очень низкими значениями младенческой смертности этот парадокс не действует.

Не нашли, что искали? Воспользуйтесь поиском по сайту: