
|
|
Порядок выполнения лабораторной работы5.1. Проверка результатов расчета домашнего задания. В окне «Контроль домашних расчетов» ввести номер варианта домашнего задания, двоичные последовательности для каждого сообщения источника, значения
5.2. Определение средней длины сообщения при передаче последовательностей, составленных из сообщений, имеющих разную вероятность появления. 5.2.1. Открыть окно блока ввода сообщения щелчком мыши. 5.2.2. В раскрывающемся списке верхней строки выбрать «алфавит из домашнего задания». 5.2.3. Составить три последовательности по 16 сообщений исходного алфавита (см. таблицу 1), полученные: - чередованием двух наиболее вероятных сообщений (например, для варианта 1 {а4, а5, а4, а5,…., а4, а5}); - повторением сообщения алфавита, вероятность появления которого равнв или наиболее близка к - повторением сообщения алфавита, вероятность появления которого минимальна (например, для варианта 1{а6, а6, а6,…., а6}). 5.2.4. Ввести соответствующую последовательность в нижнюю строку блока ввода сообщения. Для этого поместить курсор в нижнюю строку и последовательно ввести цифры, соответствующие номерам сообщений. Например: для последовательности {а4, а5, а4, а5,…., а4, а5}, следует ввести 4545…45. 5.2.5. В блоке определения длины кодовой комбинации посмотреть для каждой последовательности сообщений среднюю длину кодовой комбинации на сообщение алфавита при равномерном и эффективном кодировании; 5.3. Исследование влияния одиночной ошибки на результаты декодирования. 5.3.1. Составить и ввести произвольную комбинацию из 16 сообщений. 5.3.2. В окне блока ошибки изменить один из элементов последовательности на противоположный. В данном окне необходимо указать номер элемента, в который нужно ввести ошибку и нажать кнопку «инвертировать». В соответствующем разряде маски ошибки появится единица. 5.3.3. Переписать в отчет принятую двоичную последовательность из нижнего поля блока определения ошибочных сообщений и декодировать ее в соответствии с кодовыми комбинациями Вашего варианта. Определить количество неверно принятых сообщений. 5.3.4. Проверить правильность декодирования, используя данные из блока отображения. 5.3.5. Установить в блоке ввода сообщения «русский алфавит». 5.3.6. Ввести последовательность слов, состоящую из N букв русского алфавита, где 5.3.7. Посчитать и сравнить количество двоичных символов необходимых для передачи введенного текста при кодировании равномерным кодом и кодом Хаффмана. 5.3.8. Ввести ошибку в единичный элемент, соответствующий k-ой букве, где k – номер варианта домашнего задания. 5.3.9. Посмотреть, как расшифровывается последовательность, содержащая ошибку. Сделать выводы.
Содержание отчета 1. Результаты выполнения домашнего задания. 2. Результаты выполнения моделирования. 3. Выводы по работе. 7. Контрольные вопросы 1. Принцип формирования кодовых комбинаций при кодировании методом Хаффмана. 2. Как рассчитывается средняя длина кодовой комбинации кода Хаффмана и каково ее минимальное значение? 3. В чем состоит свойство префиксности эффективных кодов? 4. Количественные показатели эффективности неравномерного кодирования. 5. Принцип декодирования последовательности префиксного кода. 6. Принципы возникновения трека ошибок при декодировании последовательности кодовых комбинаций префиксного кода.
Литература 1. Передача дискретных сообщений: Учебник для вузов/ В.П.Шувалов, Н.В.Захарченко, В.О.Шварцман и др.; под. ред. В.П.Шувалова. – М.: Радио и связь, - 1990. – 464 с. 2. Системы мобильной связи : Учебное пособие для вузов/ В. П. Ипатов. В. К. Орлов, И. М. Самойлов, В. Н. Смирнов; под ред. В. П. Ипатова. – М.: Горячая линия – Телеком, 2003. 3. Компьютерные сети. Принципы, технологии, протоколы / В.Г. Олифер, Н.А. Олифер. - СПб.:Питер, 2002.-672 с. 4. Теория информации: Учебное пособие для вузов/ А.С. Котоусов. – М.: Радио и связь, 2003.
ЛАБОРАТОРНАЯ РАБОТА №2 Исследование методов кодирования и декодирования циклических кодов
Цель работы 1.1. Изучение структуры кодеров циклического кода. 1.2. Анализ процесса формирования проверочных разрядов. 1.3. Изучение принципов обнаружения ошибок в декодере циклического кода. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  ,
,  . Внимание! При вводе расчетных значений следует обеспечить точность расчетов до второго знака после запятой.
. Внимание! При вводе расчетных значений следует обеспечить точность расчетов до второго знака после запятой.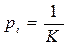 , где К – объем алфавита источника (например, для варианта 1 {а3, а3, а3,…., а3});
, где К – объем алфавита источника (например, для варианта 1 {а3, а3, а3,…., а3}); .
.