
|
|
Описание схемы и вывод рабочей формулы
Во многих случаях необходимо знать величину электрического сопротивления проводника. Наиболее распространенным методом измерения сопротивлений является метод моста.
В основе работы лежит применение 2-х правил Кирхгофа к схеме на рис. 5. II правило Кирхгофа: В любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сопротивлений участков Ri на токи Ii, протекающие по ним, равна алгебраической сумме имеющихся в контуре ЭДС.
Процесс измерения при помощи этой схемы связан с требованием равенства нулю тока в мосте. При замыкании ключа К гальванометр обнаружит наличие тока. Но можно так подобрать сопротивление Rо, R1 и R2, что потенциалы точек С и D станут равными, т.е. в цепи гальванометра ток будет отсутствовать (мост сбалансирован, стрелка гальванометра остается на нуле при замыкании ключа К). Задача состоит в определении сопротивления Rх . Для этого применим правила Кирхгофа к нашей цепи. Припишем токам направления, обозначенные на рис.7 стрелками (это делается произвольно, но в данной схеме логично выбрать направления токов, указанные на рисунке). Применяя к контурам АСДА и СВДС второе правило Кирхгофа, получим:
IxRx – I1R1 = 0 I0R0 – I2R2 = 0 (16) (т.к. э.д.с. в указанных контурах отсутствуют). Применяя к узлам С и Д первое правило Кирхгофа, поскольку ток в гальванометре отсутствует, будем иметь
I0 = Ix, I1 = I2. (17)
Из уравнений (16) и (17) получим:
Таким образом, при отсутствии тока в гальванометре можно по формуле (18) вычислить неизвестное сопротивление Rх, если известны сопротивления R0, R1 и R2.
На практике применяются реохордные мосты, у которых сопротивлением R0 служит магазин сопротивлений. Двумя другими сопротивлениями R1 и R2 являются части реохорда АВ (рис.6), имеющего подвижный контакт Д, соединенный с гальванометром Г. Этот контакт делит реохорд на две части АД и ДВ. Вследствие того, что проволока реохорда однородна и тщательно калибрована, отношение сопротивлений участков цепи АД и ДВ (плеч реохорда) можно заменить отношением соответствующих длин плеч реохорда l2 и l1:
Подставив (19) в (20), получим рабочую формулу для определения сопротивления Rх:
Измерения и обработка результатов измерений
1. Собирают электрическую схему, как показано на рис 6. Вместо сопротивления Rх в цепь включают одно из известных сопротивлений R1. 2. Помещают подвижный контакт посередине реохорда и подбирают сопротивление R0 в магазине так, чтобы ток в гальванометре Г почти исчез. 3. Окончательно устанавливают стрелку гальванометра на нулевое деление путем небольших перемещений контакта Д и производят измерение длин плеч реохорда l2 и l1. 4. Опыт повторяют 3 раза при различных значениях сопротивления магазина R0. 5. Подставляя в формулу (21) значения R0, l2 и l1, взятые из каждого отдельного опыта, вычисляют R1. 6. Вместо сопротивления R1 в цепь включают сопротивление R2. Производят с этим сопротивлением такие же измерения, как и с R1. 7. Измеренные сопротивления R1 и R2 включают в цепь вместе, сначала – последовательно (рис. 7), а затем – параллельно (рис. 8), и производят измерения. 8.
Полученные опытным путем результаты последовательного и параллельного соединения сопротивлений необходимо сопоставить с величинами сопротивлений, рассчитанными по формулам:
пользуясь значениями сопротивлений
Задачи 1. Построить график зависимости силы тока на участке цепи от напряжения, если сопротивление участка равно 200 Ом, а приложенное к нему напряжение меняется от 20 до 120 В (через 20 В).
2. Четыре проводника одинаковой длины из одного и того же материала соединены последовательно. Диаметры проводников соответственно равны 10-3 м, 2.10-3 м, 3.10-3 м, 4.10-3 м. К системе приложено напряжение 100 В. Определить падение напряжения на каждом проводнике.
3.
4. Какого сопротивление проволоки диаметром 1 мм и длиной 20 м, если сопротивление проволоки диаметром 0,6 мм и длиной 9 м, изготовленной из того же материала, равно 24 Ом? Ответы: 1) 15 Ом; 2) 30 Ом; 3) 20 Ом; 4) 8 Ом; 5) 50 Ом.
5. Какое из написанных ниже выражений не обязательно должно выполняться при уравновешенном мосте (рис. 10)? Ответы: 1) φА- φВ= φА - φD; 2) IГ = 0; 3) R1 = R2; 4) φВ = φD; 5)
Контрольные вопросы 1. Причины возникновения сопротивления в металлах. 2. Нарисуйте принципиальную схему моста Уитстона. В чем заключается равновесие моста? 3. Сформулируйте правила Кирхгофа. 4. Выведите расчетную формулу для определения сопротивления методом моста Уитстона. 5. Почему отношение сопротивления плеч реохорда можно заменить отношением длин плеч l1 и l2? 6. Запишите выражения для определения сопротивления при последовательном и параллельном соединении проводников.
Из чистых металлов наименьшим сопротивлением обладают медь, алюминий, поэтому из них делают электрические провода. Специально приготовленные сплавы обладают высоким сопротивлением.
Литература
1. Савельев И. В. Курс общей физики. М.: Наука. Т.2, 1982. § 34, 36. 2. Трофимова Т. И. Курс физики. М.: Высшая школа. 2002, § 101. 3. Бондарев Б. В., Калашников Н. П., Спирин Г. Г. Курс общей физики. М.: Высшая школа. 2003, кн. 2. § 4.3, 4.6
Лабораторная работа 2.2 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Мост постоянного тока, называемым мостом Уитстона, представляет собой замкнутый четырехугольник, сторонами которого являются сопротивления Rx, R0, R1, и R2. В одну из диагоналей четырехугольник включен гальванометр G, а в другую - источник постоянного тока ε. (рис. 1) Диагональ, содержащая гальванометр, называется мостом.
Мост постоянного тока, называемым мостом Уитстона, представляет собой замкнутый четырехугольник, сторонами которого являются сопротивления Rx, R0, R1, и R2. В одну из диагоналей четырехугольник включен гальванометр G, а в другую - источник постоянного тока ε. (рис. 1) Диагональ, содержащая гальванометр, называется мостом. . (15)
. (15) ,
,
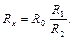 (18)
(18) Точность сравнения сопротивлений Rх и R0 будет больше, когда отношение R1/R2 близко к единице. Поэтому при измерении сопротивления при помощи моста желательно, чтобы Rх мало отличалось от R0.
Точность сравнения сопротивлений Rх и R0 будет больше, когда отношение R1/R2 близко к единице. Поэтому при измерении сопротивления при помощи моста желательно, чтобы Rх мало отличалось от R0.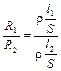 (19)
(19) (20)
(20) (21)
(21)
 , (22)
, (22)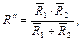 (23)
(23) и
и  , найденными ранее. Все полученные результаты сводятся в таблицу:
, найденными ранее. Все полученные результаты сводятся в таблицу:


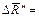


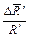




 На рис. 9 изображены графики вольтамперных характеристик двух проводников: «1» и «2». Сопротивление какого проводника больше и во сколько раз?
На рис. 9 изображены графики вольтамперных характеристик двух проводников: «1» и «2». Сопротивление какого проводника больше и во сколько раз? ; 6) нет ответа
; 6) нет ответа