Подразделение песчаных грунтов по плотности сложения

Песок	Подразделение по плотности сложения
плотный	средней плотности	рыхлый
Гравелистый, крупный и средний крупности Мелкий Пылеватый	е < 0,55 е<0,6 е<0,6	0,55≤e≤0,7 0,6 ≤e≤0,75 0,6 ≤e≤0,8	е>0,7 е>0.75 е>0,8

Таблица 3.2

Подразделение песчаных грунтов по коэффициенту водонасыщения (степени влажности) Sr

Грунт	Степень влажности
Малой степени водонасыщения (маловлажный) Средней степени водонасыщения (влажный) Насыщенные водой	0<S_r≤0,5 0,5<S_r≤0,8 0,8<S_r≤1

Таблица 3.2

Подразделение песчаных грунтов по коэффициенту

Грунт	Число пластичности, %
Супесь Суглинок Глина	1<I_p≤7 7<I_p ≤17 I_p>17

Таблица 3.4.

Подразделение пылевато-глинистых грунтов по показателю текучести

Грунт	Показатель текучести
Супесь: твердая пластичная текучая Суглинок и глина: твердые полутвердые тугопластичные мягкопластичные текучепластичные Текучие	I_L<0 0<I_L≤1 I_L>1 I_L<0 0<I_L≤0,25 0,25<I_L≤0,5 0,5<I_L≤0,75 0,75<I_L≤1 I_L>1

Таблица 3.5.

Плиты железобетонные для ленточных фундаментов под стены (по данным ЦНИИЭП жилища)

№ п/п	Марка изделия	Размеры, мм	Масса, кН	Бетон	Расход стали, кгс
		l	b	h		марка	объем, м³
1.	ФЛ8-12-2				6,8		0,274	18,2
2.	ФЛ-10-12-2				7,5		0,300	34,8
3.	ФЛ12-12-2				8,7		0,347	60,8
4.	ФЛ14-12-2				10,4		0,416	82,0
5.	ФЛ16-12-2				12,1		0,486	122,9
6.	ФЛ20-12-2				24,4		0,975	130,2
7.	ФЛ24-12-2				28,4		1,138	211,5
8.	ФЛ28-12-2				34,2		1,369	324,8
9.	ФЛ32-12-2				40,0		1,60	478,5

Таблица 3.6

Стеновые сплошные бетонные блоки (по ГОСТ 13579-78)

Марка блока	Размеры, мм	Масса, кН	Объем, м³
	l	b	h
ФБС24-3-6-Т				9,7	0,406
ФБС24-4-6-Т				13,0	0,543
ФБС24-5-6-Т				1,63	0,679
ФБС24-6-6-Т				1,93	0,815
ФБС12-4-6-Т				6,4	0,265
ФБС12-5-6-Т				7,9	0,331
ФБС 12-6-6-Т				9,6	0,398
ФБС 12-4-3-Т				3,1	0,127
ФБС 12-5-3-Т				3,8	0,159
ФБС 12-6-3-Т				4,6	0.191
ФБС9-3-6-Т				3,5	0,146
ФБС9-4-6-Т				4,7	0,195
ФБС9-5-6-Т				5,9	0,244
ФБС9-6-6-Г				7,0	0,293

ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ (2)

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ

Физические характеристики грунтов

r - плотность грунта, т/м³;

r_d - плотность грунта в сухом состоянии, т/м³;

r_s - плотность частиц грунта, т/м³;

g - удельный вес грунта,кН/м³;

g_d_-удельный вес грунта в сухом состоянии, кН/м³;

g_s_-удельный вес твердых частиц грунта кН/м³;

g_sb_- удельный вес грунта с учетом взвешивающего действия воды кН/м³;

g_{W -} удельный вес воды, равный 10 кН/м³;

W - влажность грунта природная, в долях единицы;

W_р - влажность на границе раскатывания;

W_L - влажность на границе текучести;

Физические характеристики грунтов определяют опытным путем в лабораторных условиях.

Классификационные показатели грунтов

e - коэффициент пористости грунта;

S_z - степень влажности грунта;

I_p- число пластичности грунта;

I_L - показатель текучести грунта.

Классификационные показатели определяют по расчетным формулам на основе физических характеристик грунтов.

Показатели деформируемости грунтов при сжатии

m_v - относительный коэффициент сжимаемости грунта, МПа^-I;

m₀- коэффициент сжимаемости грунта, МПа^-I;

E - модуль деформации, Мпа;

n₀ - коэффициент относительных поперечных деформаций (коэффициент Пуассона)

Показатели прочности (сопротивления сдвигу) грунтов

j - угол внутреннего трения, град;

С - удельное сцепление, кПа.

Показатели деформируемости и прочности грунтов определяются опытным путем в лабораторных или полевых условиях.

При выполнении контрольной работы все расчеты выполняются в размерности международной системы единиц (СИ). Ниже дан перевод механической системы единиц (МК ГСС) в систему СИ.

1. Сила, нагрузка, вес - I Н.

1 кгс = 9,81 Н»10Н.

1 тс = 9,81 10³Н»10кН =0,01 МН

2. Давление (напряжение):

1 кгс/см²=10 тс/м² » 100 кПа(100кН/м²) = 0,1 Мпа

3. Удельный вес:

1 тс/м² » 10кН/м²=0,01 МН/м³.

СОСТАВ И СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа предусматривает выполнение ряда расчетных задач по основным разделам дисциплины “Механика грунтов”:

-- определение природных напряжений в массиве грунта;

-- определение напряжений в массиве грунта от действия на его поверхности внешней прямоугольной нагрузки методом угловых точек;

-- расчет осадки слоя грунта под действием сплошной равномерно - распределенной нагрузки;

-- оценка устойчивости однородного откоса;

-- определение давления грунта на подпорную стену;

-- определение давления грунта на подземный трубопровод.

Контрольная работа по “Механике грунтов” подготавливает студента к расчету и проектированию транспортных сооружений.

Контрольная работа выполняется согласно индивидуальному заданию, которое содержит необходимую исходную информацию и оформляется в виде пояснительной записки с вложением в необходимых случаях графического материала, выполняемого на миллиметровой бумаге.

При решении каждой задачи необходимо приводить исходную информацию, пояснять (с приведением в необходимых используемые формульные зависимости) операции по обработке исходной информации, приводить (в соответствующих случаях) графический материал и конечные результаты решения задачи (выводы по решению задачи).

Все расчеты выполняются с использованием системы СИ – единиц. Допускается указание в скобках размерности в системе МКГС.

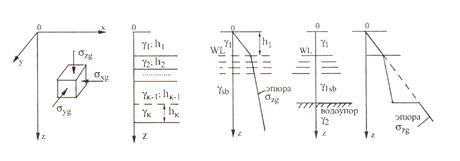
Задача № 1. Определение напряжений от собственного веса грунта (природного или бытового давления).

Напряжения от собственного веса грунта имеют значение для свеженасыпанных земляных сооружений, оценки природной уплотненности грунтов и в расчетах осадок оснований фундаментов. При горизонтальной поверхности грунта напряжения от собственного веса будут увеличиваться с глубиной.

Вертикальное напряжение от собственного веса грунта σ_zgпредставляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице.

При постоянном удельном весе грунтаγ по глубине по осиz напряжения σ_zg определяются по формуле:

σ_zg= γ z(1.1)

Рис. 1.1. Определение напряжения в грунте от собственного веса и наличия уровня грунтовых вод.

При слоистом залегании грунтов обладающих различным удельным весом или наличии грунтовых вод величина σ_zgопределяется суммированием (рис. 1.1)

σ_zg= (1.2)

Горизонтальные напряжения σ_уgи σ_хgтакже увеличиваются с глубиной и определяются по формуле

σ_хg= σ_уg=ξσ_zg (1.3)

где ξ=ν(1-ν) – коэффициент бокового давления грунта;

ν – коэффициент относительных поперечных деформаций, аналогичный коэффициенту Пуассона упругих тел.

Коэффициент Пуассона ν принимается равным для грунтов: крупнообломочных - 0,27; песков и супесей – 0,30; суглинков – 0,35; глин – 0,42.

Таблица 1.1

Варианты расчетного задания № 1

№ ва-риан-та	Грунт №1	Грунт №2
Тип грунта	Толщина слоя	кН/м³	кН/м³	Глубина уровня грунтовых вод WL	Тип грунта (водоу-пор)	Расчетная глубина определения σ_zg	кН/м³
	Песок мелкий		18,0	9,6	2,5	Глина		19,8
	Супесь		17,6	9,4	1,0	Суглинок		21,0
	Песок крупный		18,3	9,9	3,0	Глина		20,4
	Суглинок легкий	4,5	19,0	10,1	1,8	Суглинок		18,9
	Песок пылеватый		18,9	9,8	2,0	Глина		19,4
	Песок ср. круп.		19,1	10,3	2,5	Суглинок		20,8
	Супесь		18,6	10,1	2,2	Глина		21,1
	Песок мелкий		18,5	9,8	1,5	Суглинок		19,8
	Супесь		19,3	10,5	1,0	Глина		19,4
	Песок пылеватый	4,5	18,7	9,6	2,0	Суглинок		18,9
	Песок крупный	2,5	18,2	9,4	1,2	Глина		19,3
	Песок ср. круп.		19,3	10,1	2,0	Суглинок		19,9
	Суглинок	3,5	19,2	10,5	1,3	Глина		20,3
	Супесь	3,4	18,7	9,3	1,0	Суглинок	7,5	20,4
	Песок крупный	4,1	18,4	9,1	1,5	Глина	9,5	20,5
	Песок мелкий	4,5	17,9	8,9		Суглинок	10,5	19,6
	Песок пылеватый		18,4	9,6		Глина	11,0	19,1
	Песок ср. круп.	2,8	19,4	10,7	1,4	Суглинок	12,0	18,9
	Супесь	3,3	19,8	11,0	1,3	Глина	14,0	18,4
	Супесь	3,8	19,7	10,8	1,8	Суглинок	11,0	21,1
	Песок ср. круп.	4,2	18,9	9,7	2,1	Глина	12,0	20,8
	Песок пылеватый	5,2	19,8	10,1	3,0	Суглинок	7,0	20,4
	Песок крупный	5,3	19,1	10,0	2,0	Глина	6,0	20,3
	Песок пылеватый	3,9	17,5	8,1	1,5	Суглинок	7,0	19,4
	Супесь	4,8	21,1	11,5	1,4	Глина	8,0	19,8
	песок ср. круп.	4,1	19,4	11,1	2,4	Суглинок	9,0	19,3
	Супесь	3,8	18,7	9,8	2,8	Глина	10,0	19,2

Вариант задания определяется по сумме трех последних цифр шифра студента.

Используя исходные данные для конкретного варианта (табл.1.1) строится эпюра напряжений σ_zg от собственного веса грунта.

ПРИМЕР РАСЧЕТА. Требуется определить напряжения от собственного веса грунта на глубине 6 м от поверхности. Основание до глубины 3 м сложено песком средней крупности и средней плотности γ₁=19 кН/м³, γ_sb=10,3 кН/м³. Песок подстилается слоем глины полутвердой γ₂=22 кн/м² являющейся водоупором. Уровень грунтовых вод WL расположен в песке на глубине 2 м от поверхности.

В точке 1 на глубине 2 м	σ_zg1=2·19=38 кН/м³=38 кПа.
В точке 2 на глубине 3 м	σ_zg2=38+1·10,3=48,3 кПа.
В точке 2^/ на глубине 3 м	σ_zg2^/=38+1·19=57 кПа.
В точке 3 на глубине 6 м	σ_zg3=57+3·22=123 кПа.
В точке 3 на глубине 6 м	σ_хg= σ_уg=[(0,42/(1-0,42)] ·123=89 кПа.

Результаты расчеты представляются на графике (рис.1.2)

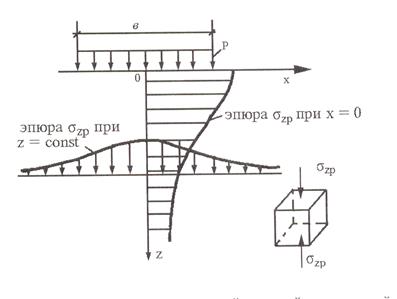
Задача №2. Определение напряжений в грунтовом основании от действия прямоугольной нагрузки приложенной на его поверхности.

Определение напряжений в грунтовой толще от действия внешних нагрузок необходимо для установления условий прочности и устойчивости грунтов, определения деформаций и осадок оснований фундаментов.

В большинстве практических случаев при решении вопроса о распределении напряжений в грунтах в механике грунтов применяют теорию линейно деформируемых тел. Для определения напряжений по этой теории будут полностью справедливы уравнения теории упругости, также базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука).

Определение сжимающих напряжений от действия прямоугольной нагрузки в произвольной точке основания производится на основе метода угловых точек. Значение величин сжимающих напряжений для угловых точек прямоугольной площади загрузки позволяет очень быстро вычислить сжимающие напряжения для любой точки полупространства (грунтового основания) если пользоваться значениями угловых коэффициентов α и α_с.

Для точек расположенных по вертикальной оси под центром загруженного прямоугольника сжимающие напряжения σ_zр= αр

А для точек расположенных по вертикальной оси под углом загруженного прямоугольника

σ_zрс= α_ср

где α – коэффициент, принимаемый по таблице в зависимости от соотношения сторон η=l/b прямоугольной нагрузки (формы подошвы фундамента) и относительной глубины, равной:

ξ=2z/b – при определении σ_zр.

α_с= α/4 – коэффициент, при определении α в данном случае по таблице 2.1 η=l/b, а относительная глубина ξ=z/b.

Характерный вид эпюр σ_zрпоказан на рисунке 2.1.

Рис. 2.1. Эпюра сжимающих напряжений σ_zр от дествия внешней равномерно-распределенной прямоугольной нагрузки

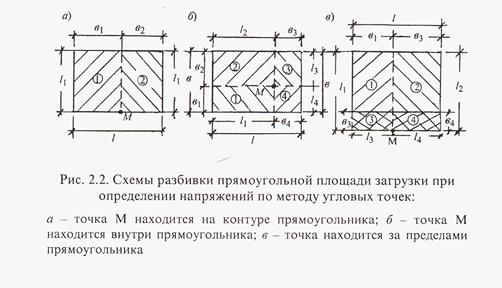
Метод угловых точек для определения сжимающих напряженийσ_zрприменяют в случае, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда сжимающее напряжение в этой точке на любой глубине будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.

Рассмотрим три основных случая:

1) Точка М находится на контуре прямоугольника внешних воздействий (рис. 2.2а);

2) Точка М находится внутри прямоугольника давлений

(рис. 2.2б);

3) Точка М находится вне прямоугольника давлений (рис. 2.2в).

В первом случае величина σ_z_рна заданной глубине z под точкой М определяется как сумма двух угловых напряжений, соответсивующих прямоугольника 1 и 2, т.е.:

σ_z_рм=(α_с1+α_с2)р

Во втором случае необходимо суммировать угловые напряжения от четырех прямоугольных площадей загрузки 1,2,3,4:

σ_z_рм =(α_с1+α_с2+α_с3+α_с4)р

В третьем случае напряжение в точке М складывается из суммы напряжений от действия нагрузки по прямоугольникам 1 и 2, взятых со знаком “плюс”, и напряжений от действия нагрузки по прямоугольникам 3 и 4, взятых со знаком “минус”

σ_z_рм =(α_с1+α_с2-α_с3-α_с4)р

Используя исходные данные для конкретного варианта (табл.2.2) определяются напряжения σ_z_рпод центром и под серединой длинной стороны загруженного прямоугольника в трех точках по глубине основания z=0,5b; 1,0b и 2b и строятся эпюры напряжений.

Таблица 2.1.

Значение коэффициента α для расчета

Предыдущая 1 2 345 6 7 8 Следующая

Не нашли, что искали? Воспользуйтесь поиском по сайту: