
|
|
Советы по подготовке к зачетуПри подготовке к зачету особое внимание следует обратить на следующие моменты. На зачет выносятся лишь основные профессионально-значимые вопросы криминологии с целью проверить умение самостоятельно осмысливать криминологические явления в их современной научной трактовке и готовность к практическому применению криминологических знаний. Поэтому рекомендуется применять на текущих занятиях метод самопроверки по всем вопросам, своевременное выявление и устранение слабостей. Залогом успешного изучения криминологии, интереса к ней является понимание значения криминологических знаний для успешной практической деятельности правоохранительных органов. Студенты должны хорошо усвоить сущность таких свойств преступности, как латентность и ее причины, виктимность и формы виктимного поведения, мера и "цена" преступности, ее география, масштаб распространения и способность к самовоспроизводимости. Необходимо уметь производить расчеты уровня, структуры и динамики преступности с применением формул, приемов, расчетов. Для того, чтобы избежать трудностей при ответах, рекомендуется внимательно ознакомится с приведенным в разделе 4 глоссарием и посмотреть рекомендуемую литературу, приведенную в списке основных и дополнительных источников к семинарским занятиям. Раздел 3. Материалы тестовой системы или практикум по решению задач по темам лекций В разделе 1 настоящего комплекса предложено решить практические задачи по расчету криминологических показателей. Ниже даны примеры решения некоторых заданий. Пример № 1.Определите средний рост числа рассмотренных дел судьёй, вычислив показатели темпа роста и среднюю геометрическую и составьте прогноз на 2012 год, если количество рассмотренных судьей дел в 2009 г. = 30, 2010 г. = 45, 2011 г. = 60 и в 2012 г. = 75. Решение: Сначала вычислим показатели темпа роста по отношению к предыдущему периоду. В данном случае их три: Х1=45 : 30 = 1,5; Х2 = 60: 45 = 1,3; Х3 = 75: 60 = 1,25. Средняя геометрическая определяется по формуле:
Прогноз на 2010 год – это среднеарифметическая = (30 + 45 + 60 + 75) : 4 = 52,5 = 53 дела. Пример № 2.Допустим,сроки лишения свободы были таковы: в 2006 году = 1 год, в 2007 г. = 2 года, в 2008 г. = 3, в 2009 г.= 4 и в 2010 г. = 5 лет. Составьте прогноз на 2012 год. Решение: Прогноз на 2012 год равен определению среднего срока (средней арифметической). Он равен 3 годам (1 + 2 + 3 + 4 + 5 : 5 = 3).
Для облегчения работы студентом при расчете криминологических показателей ниже приведены формулы их расчета. Необходимые Формулы: Коэффициент преступностирассчитывается по формуле: где КП – коэффициент преступности,П – абсолютное число учтённых преступлений, Н – абсолютная численность населения.
Коэффициент поражённости населения преступниками: где Л – лица, совершившие преступления (с 14 лет); Н – население за минусом лиц до 14 лет. Коэффициент интенсивности: Индекс тяжести преступлений (или видовой индекс): где Итп – индекс тяжести преступлений; Σ Пт – сумма преступлений текущего периода; Σ Пб – сумма преступлений базового периода; Вт – баллы тяжести преступлений (одинаковые и для текущего, и для базового периода). Совокупный или тотальный индекс: Jm = Σ (преступления умножить на их условную оценку) одного года Σ (преступления умножить на их условную оценку) другого года Показатель структуры преступности: где СП – структура преступности, Вп – вид преступления; П – количество преступлений.
Темпы роста – изменения преступности во времени с учётом 100 %.
Темп прироста:
Средняя геометрическая:
Среднее квадратическое отклонение: где σ – среднеквадратическое отклонение, Х – величина варианта ряда,
Коэффициент вариации: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
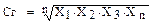
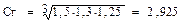
 ,
, ,
, , где П – абсолютное число правонарушений, Е – единица населения, Н – его численность
, где П – абсолютное число правонарушений, Е – единица населения, Н – его численность ,
, , при этом Σ Вп = 100 %.
, при этом Σ Вп = 100 %. ,где П1 – год младший, П2 – год старший по цифре.
,где П1 – год младший, П2 – год старший по цифре.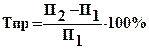 (может быть «–» числом).
(может быть «–» числом). Средняя арифметическая простая = деление суммы всех величин на их число.
Средняя арифметическая простая = деление суммы всех величин на их число.
 , где Х – показатель роста за соответствующий период.
, где Х – показатель роста за соответствующий период.
 – среднеарифметическая ряда, ∑ - сумма, n – число вариантов.
– среднеарифметическая ряда, ∑ - сумма, n – число вариантов.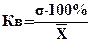 ,
,  где Кв – коэффициент вариации, σ – среднеквадратическое отклонение,
где Кв – коэффициент вариации, σ – среднеквадратическое отклонение,