
|
|
Сети с прямой передачей сигналаОднослойная сеть с S нейронами с функциями активации logsig, имеющая R входов, показана на рис. 2.14.
Эта сеть, не имеющая обратных связей, называется сетью с прямой передачей сигнала. Такие сети часто имеют один или более скрытых слоев нейронов с сигмоидальными функциями активации, в то время как выходной слой содержит нейроны с линейными функциями активации. Сети с такой архитектурой могут воспроизводить весьма сложные нелинейные зависимости между входом и выходом сети. Для пояснения обозначений в многослойных нейронных сетях внимательно изучите двухслойную сеть, показанную на рис. 2.15
Эта сеть может быть использована для аппроксимации функций. Она может достаточно точно воспроизвести любую функцию с конечным числом точек разрыва, если задать достаточное число нейронов скрытого слоя. Создание, инициализация и моделирование сети Формирование архитектуры сети Первый шаг при работе с нейронными сетями – это создание модели сети. Для создания сетей с прямой передачей сигнала в ППП NNT предназначена функция newff. Она имеет 4 входных аргумента и 1 выходной аргумент – объект класса network. Первый входной аргумент – это массив размера R´2, содержащий допустимые границы значений (минимальное и максимальное) для каждого из R элементов вектора входа; второй – массив для задания количества нейронов каждого слоя; третий – массив ячеек, содержащий имена функций активации для каждого слоя; четвертый – имя функции обучения. Например, следующий оператор создает сеть с прямой передачей сигнала: net = newff([–1 2; 0 5],[3,1],{'tansig','purelin'},'traingd'); Эта сеть использует 1 вектор входа с двумя элементами, имеющими допустимые границы значений [–1 2] и [0 5]; имеет 2 слоя с тремя нейронами в первом слое и одним нейроном во втором слое; используемые функции активации: tansig – в первом слое, purelin – во втором слое; используемая функция обучения – traingd. М-функция newff не только создает архитектуру сети, но и инициализирует ее веса Инициализация сети После того как сформирована архитектура сети, должны быть заданы начальные net = init(net); Способ инициализации зависит от выбора параметров сети net.initFcn и net.layers{i}.initFcn, которые устанавливают ту или иную функцию инициализации. Параметр net.initFcn Для сетей с прямой передачей сигнала обычно применяется одна из двух функций инициализации слоя: initwb или initnw. Функция initwb позволяет использовать собственные функции инициализации для каждой матрицы весов входа и вектора смещений, задавая параметры net.inputWeights{i, j}.initFcn Функция initnw применяется для слоев, использующих сигмоидальные функции активации. Она генерирует начальные веса и смещения для слоя так, чтобы активные области нейронов были распределены равномерно относительно области значений входа. Это имеет несколько преимуществ по сравнению со случайным распределением весов и смещений: во-первых, избыток нейронов минимален, поскольку активные области всех нейронов соответствуют области значений входа, во-вторых, обучение выполняется быстрее, так как для каждой области значений входа найдутся нейроны с той же областью определения аргумента. В рассмотренном выше примере создания сети с прямой передачей сигнала метод init вызывается автоматически при обращении к М-функции newff. Поэтому инициализация сети выполняется по умолчанию. Если же пользователь хочет применить специальный метод инициализации или принудительно установить значения весов и смещений, то он может непосредственно обратиться к функции init. Например, если мы хотим заново инициализировать веса и смещения в первом слое, используя функцию rands, то надо ввести следующую последовательность операторов: net.layers{1}.initFcn = 'initwb'; net.inputWeights{1,1}.initFcn = 'rands'; net.biases{1,1}.initFcn = 'rands'; net.biases{2,1}.initFcn = 'rands'; net = init(net); Моделирование сети Статические сети. Статическая нейронная сеть характеризуется тем, что в ее составе нет элементов запаздывания и обратных связей. Ее поведение не зависит от типа вектора входа, поскольку последовательно подаваемые векторы можно рассматривать как действующие одновременно или как один объединенный вектор. Поэтому в качестве модели статической сети рассмотрим сеть, показанную на рис. 2.16.
Это однослойная сеть с двухэлементным вектором входа и линейной функцией активации. Для задания такой сети предназначена М-функция newlin из ППП Neural Network Toolbox, которая требует указать минимальное и максимальное значение для каждого % Формирование однослойной линейной сети net с двухэлементным % входным сигналом со значениями от –1 до 1 net = newlin([–1 1;–1 1],1); Определим весовую матрицу и смещение равными W= [1 2], b = 0, и зададим эти значения, используя описание структуры сети net.IW{1,1} = [1 2]; % Присваивание значений весов net.b{1} = 0; % Присваивание значения смещения Предположим, что на сеть подается такая последовательность из четырех векторов входа:
Поскольку сеть статическая, можно перегруппировать эту последовательность в следующий числовой массив: P = [–1 0 0 1; 0 –1 1 –1]; Теперь можно моделировать сеть: A = sim(net,P) % Моделирование сети net с вектором входа P и выходом A A = –1 –2 2 –1 Результат нужно интерпретировать следующим образом. На вход сети подается Динамические сети. Когда сеть содержит линии задержки, вход сети надо рассматривать как последовательность векторов, подаваемых на сеть в определенные моменты времени. Чтобы пояснить этот случай, рассмотрим простую линейную сеть, которая содержит 1 элемент линии задержки (рис. 2.17).
Построим такую сеть: % Создание однослойной линейной сети с линией задержки [0 1] net = newlin([–1 1],1,[0 1]); Зададим следующую матрицу весов W= [1 2] и нулевое смещение: net.IW{1,1} = [1 2]; % Присваивание значений весов net.biasConnect = 0; % Присваивание значений смещений Предположим, что входная последовательность имеет вид {–1, –1/2, 1/2, 1}, и зададим ее в виде массива ячеек P = {–1 –1/2 1/2 1}; Теперь можно моделировать сеть, используя метод sim: A = sim(net,P) % Моделирование сети net с входным сигналом P и выходом A A = [–1] [–5/2] [–1/2] [2] Действительно,
Введя массив ячеек, содержащий последовательность входов, сеть сгенерировала массив ячеек, содержащий последовательность выходов. В данном случае каждый выход формируется согласно соотношению a(t) = p(t) + 2p(t–1). (2.9) При изменении порядка следования элементов во входной последовательности будут изменяться значения на выходе. Если те же самые входы подать на сеть одновременно, то получим совершенно иную реакцию. Для этого сформируем следующий вектор входа: P = [–1 –1/2 1/2 1]; После моделирования получаем: A = sim(net,P) % Моделирование сети A = –1 –1/2 1/2 1 Результат такой же, как если применить каждый вход к отдельной сети и вычислить ее выход. Поскольку начальные условия для элементов запаздывания не указаны, то по умолчанию они приняты нулевыми. В этом случае выход сети равен
Если требуется моделировать реакцию сети для нескольких последовательностей сигналов на входе, то надо сформировать массив ячеек, размер каждой из которых совпадает с числом таких последовательностей. Пусть, например, требуется приложить к сети 2 последовательности:
Вход P в этом случае должен быть массивом ячеек, каждая из которых содержит два элемента по числу последовательностей P = {[–1 1] [–1/2 1/2] [1/2 –1/2] [1 –1]}; Теперь можно моделировать сеть: A = sim(net,P); % Моделирование сети net с входным сигналом P и выходом A Результирующий выход сети равен A = {[–1 1] [–5/2 5/2] [–1/2 1/2] [2 –2]} В самом деле, {
На рис. 2.18 показан формат массива P, представленного Q выборками (реализациями), при моделировании сети.
В данном случае это массив ячеек с одной строкой, каждый элемент которой объединяет Q реализаций вектора p – [p1(TS), p2(TS), …, pQ(TS)] – для некоторого момента времени TS. Если на вход сети подается несколько векторов входа, то каждому входу будет соответствовать 1 строка массива ячеек. Представление входов как массива ячеек соответствует последовательному представлению наблюдаемых данных во времени. Представление вектора входа может быть интерпретировано иначе, если сформировать временные последовательности для каждой реализации, как это показано на рис. 2.18. Тогда можно говорить о том, что на вход сети подается Q выборок из интервала времени [1, TS], которые могут быть описаны числовым массивом P вида P = [[p1(1), p1(2), …, p1(TS)]; [p2(1), p2(2), …, p2(TS)]; … Представление входов как числового массива выборок в формате double соответствует групповому представлению данных, когда реализации вектора входа для всех значений времени на интервале выборки обрабатываются потоком. Обучение нейронных сетей При решении с помощью нейронных сетей прикладных задач необходимо собрать достаточный и представительный объем данных для того, чтобы обучить нейронную сеть решению таких задач. Обучающий набор данных – это набор наблюдений, содержащих признаки изучаемого объекта. Первый вопрос, какие признаки использовать и сколько Выбор признаков, по крайней мере первоначальный, осуществляется эвристически на основе имеющегося опыта, который может подсказать, какие признаки являются наиболее важными. Сначала следует включить все признаки, которые, по мнению аналитиков или экспертов, являются существенными, на последующих этапах это множество будет Нейронные сети работают с числовыми данными, взятыми, как правило, из некоторого ограниченного диапазона. Это может создать проблемы, если значения наблюдений выходят за пределы этого диапазона или пропущены. Вопрос о том, сколько нужно иметь наблюдений для обучения сети, часто оказывается непростым. Известен ряд эвристических правил, которые устанавливают связь между количеством необходимых наблюдений и размерами сети. Простейшее из них гласит, что количество наблюдений должно быть в 10 раз больше числа связей в сети. На самом деле это число зависит от сложности того отображения, которое должна воспроизводить нейронная сеть. С ростом числа используемых признаков количество наблюдений возрастает по нелинейному закону, так что уже при довольно небольшом числе признаков, скажем 50, может потребоваться огромное число наблюдений. Эта проблема носит название "проклятие размерности". Для большинства реальных задач бывает достаточным нескольких сотен или тысяч наблюдений. Для сложных задач может потребоваться большее количество, однако очень редко встречаются задачи, где требуется менее 100 наблюдений. Если данных мало, то сеть не имеет достаточной информации для обучения, и лучшее, что можно в этом случае сделать, – это попробовать подогнать к данным некоторую линейную модель. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 2.14
Рис. 2.14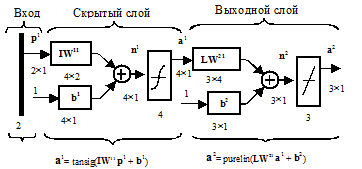 Рис. 2.15
Рис. 2.15 Рис. 2.16
Рис. 2.16 (2.7)
(2.7) Рис. 2.17
Рис. 2.17 (2.8)
(2.8) . (2.10)
. (2.10) (2.11)
(2.11) ,
,  ,
,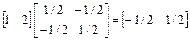 ,
,  }
} Рис. 2.18
Рис. 2.18