
|
|
СД.04.6. Оптимизация режимов ЭЭС, содержащих ТЭС и ГЭС.Наивыгоднейшее распределение нагрузки при постоянстве напора; на ГЭС. Определение множителей α. Задача оптимизации режимов энергосистем с ГЭС, имеющих водохранилища, является вариационной задачей. Вариационными задачами называются задачи исследования на экстремум функционалов, т. е. величин, численное значение которых определяется выбором одной или нескольких функций. В случае оптимизации режима энергосистемы с ГЭС функционалом будет расход топлива на тепловых электростанциях, определяющийся графиками работы ТЭС за цикл регулирования при выполнении изопериметрических условий расходования заданного объема воды на ГЭС. Задача может быть решена методом неопределенных множителей Лагранжа Математически задача формулируется следующим образом: найти графики нагрузки п ТЭС и т ГЭС, обеспечивающие за цикл регулирования минимум расхода топлива по системе в целом
при соблюдении баланса активных мощностей для каждого момента времени
и изопериметрических условий расходования заданного объема воды на каждой ГЭС за цикл регулирования:
Составляем функцию Лагранжа:
В качестве независимых переменных принимаем нагрузки тепловых Pit и гидростанций Рjt. Дифференцирование по независимым переменным дает:
Обозначая ОПР воды
Как видно, условием минимума расхода топлива будет равенство относительных приростов расхода топлива на ТЭС и относительных приростов расхода воды на ГЭС, умноженных на соответствующие множители Лагранжа αj. Неопределенный множитель λt, представляющий собой общесистемный относительный, прирост, зависит от суммарной нагрузки и, в общем случае, изменяется с течением времени. Множители αj, постоянные в течение цикла регулирования для каждой ГЭС, характеризуют энергетическую ценность воды, Действительно, из (7) получаем
Другими словами, величина αj равна изменению расхода топлива на тепловых электростанциях при изменении расхода воды на ГЭС на единицу При учете изменения напора выбор экономического режима усложняется ввиду того, что режим работы ГЭС в любой момент времени влияет на последующий. Так, увеличение расходе воды в какой-либо момент времени вызывает увеличение сработки водохранилища и повышение отметки нижнего бьефа, т. е. снижает напор в последующие часы. Однако и эта вариационная задача может быть решена как задача на отыскание минимума функции многих независимых переменных. Для этого цикл регулирования разбиваетсй на Т интервалов, в течение каждого из которых предполагаются неизменными значения нагрузок ТЭС Рit, расходов воды Wjt и напоров на ГЭС Нjt, но сохраняется влияние режима в интервале t на все последующие от t+ 1 до Т. Целевая функция имеет вид:
Условия связи будут, аналогичны выражениям (2) и (3). В качестве независимых переменных принимаем нагрузки ТЭС Pit и расходы воды на ГЭС Wjt(для всех интервалов t). Функция Лагранжа
Дифференцирование „по независимым Рit дает выражение (5) и условие (7), а по Wjt, выражение
Решая (8) относительно λt, получим
Анализ условий наивыгоднейшего распределения нагрузки (7) и (9) показывает, что принцип равенства относительных приростов сохраняется, но для ГЭС коэффициент при относительном приросте расхода воды состоит из двух частей: постоянной, представляющей собой множитель Лагранжа αj, и переменной ∆αjt, зависящей от времени, и равной
Таким образом, учет изменения напора сводится прежде всего к введению переменной во времени поправки ∆αjt, определяющей влияние последействия изменения режима. Наряду с этим необходимо принимать во внимание и зависимость характеристик относительных приростов от напора Эти два фактора оказывают противоположное влияние, что позволяет в некоторых случаях не учитывать изменения напора, а вводить в расчет его среднее значение и считать множители Лагранжа αj постоянными в течение всего цикла регулирования.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (i=1,2,…n) (1)
(i=1,2,…n) (1) (2)
(2) ,(j=1,2,…m) (3)
,(j=1,2,…m) (3) (4)
(4) ,(i=1,2,…n) (5)
,(i=1,2,…n) (5) ,(j=1,2,…m) (6)
,(j=1,2,…m) (6) и вводя принятые ранее обозначения производных, получим
и вводя принятые ранее обозначения производных, получим ;
;  .(7)
.(7)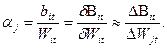
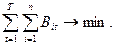
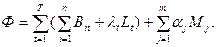
 (8)
(8) (9)
(9)