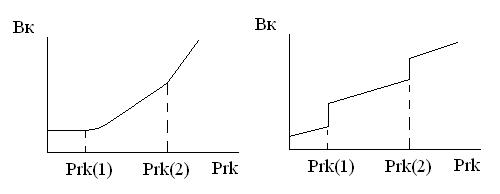
СД.04.5. Задача оптимизации режима ЭЭС по активной мощности – принцип равенства относительных приростов, коэффициенты потерь и методы их расчета.

Оптимизация режима электроэнергетической системы по активной мощности часто решается как самостоятельная важная подзадача оптимизации режима. Оптимальный ре­жим соответствует минимуму эксплуатационных затрат на производство электроэнергии в текущий момент времени. Переменная часть эксплуатационных затрат (издержек на производство электроэнергии) —это суммарный расход условного топлива на станциях энергосистемы или суммарные затраты на топливо.

В качестве целевой функции выберем суммарные затра­ты на топливо в энергосистеме.

Каждая k-я станция в энергосистеме характеризуется расходом топлива в единицу времени, зависящим от значе­ния генерируемой активной мощности Вk(Рk). Эта зависимость, вид которой приведен на рис.1, называется

обычно расходной характеристикой тепловой электростан­ции.

Рис. 13.3. Расходная характеристика (а) и характеристика относитель­ных приростов (б) типовой электростанции

Будем считать, что расход топлива Вkи затраты на то­пливо k-й станции Иk явно зависят только от активной ге­нерируемой мощности этой станции Рrk, а от остальных параметров — лишь постольку, поскольку они влияют на ак­тивную генерируемую мощность станции, т. е.

Иk= Иk(Рrk), Вk= Вk(Рrk).

Оптимальным будем считать режим, обеспечивающий минимум суммарных издержек на топливо в энергосистеме:

И=Иk(Рrk)=ЦkВk(Рrk), (1)

где Цk — цена тонны условного топлива k-й станции; Вk — часовой расход условного топлива; Вk(Рrk)— расходная характеристика k-й станции.

Задача заключается в нахождении мощностей энергообъектов (электростанций или генераторных групп) Рrk (k=1,…,m), реализующих минимум функции (1) при условии, что все переменные Рrkдолжны удовлетворять уравнению баланса Р.

Оптимизация Рrk без учета ограничений на Р станций и линий. В простейшей форме в качестве уравнений режима баланс активной мощности в системе учитывается в следующим виде:

Рrk-Рнk-∆РΣ=0, (2)

где Рrk, Рнk — соответственно генерируемая и потребляемая мощности в узлах энергосистемы; ∆РΣ — потери активной мощности в системе; т—число электростанций, включая балансирующую; (n+1)-число узлов в энергосистеме, причем в каждом из них задана постоянная нагрузка Рнk. Оптимизация Р станций при соблюдении баланса Р для. системы в целом без учета потерь мощности соответствует предположению, что ∆РΣ и Рнk постоянны. Если для целевой функции (1) и ограничения (2) записать функцию Лагранжа, то получим следующие условия опти­мальности:

k=1,…, m (3) и уравнение баланса (2).

Оптимизация Р станций без учета потерь соответствует равенству частных производных целевой функции (стоимо­сти топлива) по мощности данной станции при соблюдении баланса мощностей в системе (2). Частная производная называется относительным приростом стоимости топлива и обозначается .

= = ,

где Цk-цена топлива на k-й станции; βk - относительный прирост расхода топлива на k-й станции.

Зависимость относительного приростаот мощности может быть получена дифференцированием расходной ха­рактеристики. Обычно в качестве исходных данных при оп­тимизации принимаются именно эти зависимости, называемые характеристиками относительных приростов. Пример такой характеристики приведен на рис. 1, б. Эти зависимости из-за наличия изломов в расходных характери­стиках обычно имеют разрывы первого рода (на рис. 1, б в точках Рrk(1) иРrk(2)).

Оптимизация Р станций при соблюдении баланса Р для системы в целом с учетом потерь мощности, т. е. задача (1), (2) при учете зависимости потерь ∆РΣ от мощ­ностей станций Рrk, также решается по методу Лагранжа. В этой задаче для всех станций, кроме балансирующей, ус­ловие оптимальности (3) заменяется на следующее:

при k=1,…m-1,

где-относительный прирост потерь мощности k-й станции.

Учет технических ограничений по активной мощности станций и линийсостоит в том, что определяемые в результате оптимизации мощности станций должны быть в допустимых пределах, а мощности линий меньше их пропускных ; способностей с учетом запаса. В этом случае при оптими­зации Р станций надо учитывать не только баланс Р для системы в целом или для каждого узла, но и ограничения неравенства на мощности станций и пропускные способности линий. При учете этих ограничений-неравенств распределение Р между станциями становится задачей нелинейного математического программирования.

Не нашли, что искали? Воспользуйтесь поиском по сайту: