
|
|
СД.04.4.Общая постановка задач оптимизации установившегося режима ЭЭС как задачи математического программирования – целевая функция, ограничения в виде равенств и неравенств.Метод неопределенных множителей Лагранжа. Задача нахождения экстремума функции многих переменных может быть решена методами вариационного исчисления, в частности— методом неопределенных множителей Лагранжа. Запишем в общем виде выражение величины, экстремум которой мы ищем. Допустим, что это суммарный расход топлива
Функция, экстремум которой мы стремимся найти, носит название целевой функции или функции цели. Уравнения, определяющие условия, при выполнении которых должна быть решена задача, называются уравнениями связи. В данном случае таким уравнением является условие баланса нагрузки. Оно записывается в такой форме:
Наличие уравнений связи накладывает ограничения на решение задачи. В нашем случае ограничение имеет вид равенства. Учет ограничения вида неравенства рассмотрен ниже. Далее составляется функция Лагранжа. Она представляет собой сумму целевой функции и уравнений связи, введенных с некоторыми, пока неопределенными, , множителями
Так как выражение в скобках равно нулю, то минимум функции. Лагранжа совпадает с минимумом целевой функции и будет иметь место при одних и тех же значениях независимых переменных. Если бы ограничение (2) отсутствовало, то мы нашли бы абсолютный минимум целевой функции. В нашем случае это было бы тривиальное решение задали ВΣ=0, не имеющее практической ценности. Решая задачу с учетом ограничений, мы найдем относительный минимум. Дифференцируем функцию Лагранжа по всем независимым переменным, считая неопределенный множитель постоянным, и приравниваем частные производные нулю:
Так как частные производные от расхода топлива по нагрузке -относительные приросты расхода топлива, то получим
Уравнения (5) выражают принцип равенства относительных приростов для группы параллельно работающих агрегатов. Если бы мы имели m уравнений связи, то надо было бы ввести m неопределенных множителей. Тогда п уравнений (5) и т уравнений связи вида (2) дали бы возможность найти п+т неизвестных -нагрузок Pi и множителей εj (j= 1, . .., т). При решении задачи предполагается, что функции Вi (Pi,) — расходные характеристики — дифференцируемы. Учет ограничений вида неравенств. Практически во всех случаях решения задачи распределения нагрузки между агрегатами приходится учитывать ограничения вида неравенств. Простейшим примером является, требование, чтобы нагрузка каждого агрегата была не меньше минимально допустимой и не больше максимально допустимой (или номинальной) для данного агрегата. Pimin≤Pi≤Pimax. (6) Классические методы вариационного исчисления не дают нам приема, с помощью которого можно было бы находить экстремум функции при наличии ограничений вида неравенств. Практически подобные задачи решаются последовательным исключением переменных, вышедших за пределы, установленные теми или иными неравенствами. Допустим, что решение задачи, описанной выше, показало, что в оптимальном режиме Pkопт>Рkмакс и Ptопт>Рtмакс. Тогда этим агрегатам задаются максимально допустимые нагрузки, а между остальными агрегатами распределяется нагрузка РΣ-(Рkмакс+Рtмакс) Так как эта величина больше, чем РΣ-(Рkопт+Рtопт), то может оказаться, что для агрегата r условие (6) не будет выполнено, т. е. Prопт>Рrмакс. Тогда этому агрегату также задается максимальная нагрузка, а между оставшимися п-3 агрегатами распределяется нагрузка РΣ-(Рkмакс-Рtмакс- Рrмакс). Приближенное аналитическое решение задачи нахождения экстремума функции нескольких независимых переменных при ограничениях вида неравенств может быть найдено с помощью тех или иных искусственных приемов. Ограничения в форме неравенств могут быть учтены при решении оптимизационных задач с помощью так называемых штрафных функций. Если нагрузка агрегата Р не должна быть меньше минимально допустимой и больше максимально допустимой величины, то в выражение целевой функции можно ввести функцию, равную нулю при соблюдении неравенства (6) и принимающую произвольно большие значения при нарушении его. Тогда нагружение рассматриваемого генератора сверх Рмакс или разгрузка его ниже Рмин будет настолько экономически нецелесообразной, что выгоднее передать, в одном случае, часть нагрузки на другие агрегаты или, в другом случае, снять с них часть нагрузки, чтобы догрузить рассматриваемый генератор до Рмин. При этом целевая функция имеет вид
Здесь сi и Вi -цена и расход топлива агрегата i, а Ψi-штрафная функция, учитывающая ограничения, накладываемые на нагрузку i-го агрегата. Дифференцируя функцию Лагранжа по нагрузкам, получим
где ε —множитель Лагранжа, определяемый уравнением баланса нагрузки, (2),

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1) (2)
(2) .(3)
.(3) , (i=1,…,n). (4)
, (i=1,…,n). (4) , (i=1,…,n). (5)
, (i=1,…,n). (5)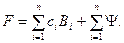
 ,(i=1,…n)
,(i=1,…n) -частная производная штрафной функции.
-частная производная штрафной функции.