|
|
Особые случаи применения симплекс-метода1.9.1 Вырожденное оптимальное решение
В тех случаях, когда проверка допустимости не приводит к однозначной идентификации переменной, подлежащей исключению из базиса, выбор такой переменной можно осуществлять произвольно. Однако на следующей итерации по крайней мере одна из базисных переменных должна быть равна нулю. В таком случае говорят, что новое решение является вырожденным. Наличие вырожденного решения не свидетельствует о какой-либо «опасности» для исследователя и вызывает лишь некоторое неудобство в теоретическом отношении. С практической точки зрения специфика ситуации целиком объясняется наличием в модели по крайней мере одного избыточного ограничения.
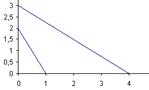
Пример 2.

     
Вырожденная точка = оптимальной точке
Значение целевой функции не меняется
1.9.2 Промежуточное вырожденное решение
В отличие от случая 1.9.1 в данном случае на следующей итерации вырожденность уже не имеет места, причем значение целевой функции улучшается.

1.9.3 Бесконечное множество решений
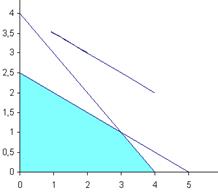
Особенность этого случая заключается в том, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей одному из связывающих ограничений. Появление в результирующей строке нулевого значения небазисной переменной свидетельствует о том, что ее включение в базис не изменит значения целевой функции, но приведет к изменению значений других переменных. Поэтому две последовательные итерации позволяют определить концы отрезка, каждая точка которой является оптимальным решением. Пример 3.
    
       
1.9.4 Неограниченные решения
Условия некоторых ЗЛП могут допускать бесконечное увеличение значений переменных без нарушения наложенных ограничений. Это свидетельствует о том, что пространство решений по крайней мере в одном направлении не ограничено. Следовательно, в таких случаях целевую функцию можно сделать сколь угодно большой или сколь угодно малой. Неограниченность решения ЗЛП свидетельствует только об одном: разработанная модель недостаточно точна. Бессмысленность использования модели, прогнозирующей «бесконечную» прибыль, вполне очевидна. Наиболее типичные ошибки, приводящие к построению моделей такого рода, состоит в том, что а) не учтено одно (или несколько) ограничение, не являющееся избыточным; б) неточно оценены параметры , фигурирующие в некоторых ограничениях.
Пример 4. (Неограниченная целевая функция.)
 (4) (4)
          
Замечание: признак неограниченности решения можно было заметить еще при первой итерации, а именно, в столбце для
Пример 5. (Пространство решений не ограничено, а оптимальное значение целевой функции конечно)

Замечание: признак неограниченности решения можно было заметить еще при первой итерации, а именно, в столбце для
1.9.5 Отсутствие допустимых решений
Если ограничения ЗЛП одновременно выполняться не могут, то задача не имеет допустимых решений. Если задача содержит ограничения в виде (=), (
Пример 6.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
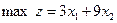 в стандартной форме
в стандартной форме 


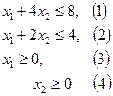
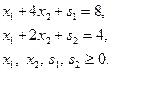




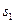


 - вырожденная оптимальная точка.
- вырожденная оптимальная точка.
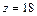




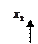




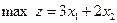 В стандартной форме
В стандартной форме 
 (1)
(1) 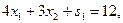
 , (2)
, (2) 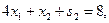
 , (3)
, (3)  ,
, , (4)
, (4) 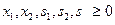
 (5)
(5)


 - вырожденное неоптимальное решение
- вырожденное неоптимальное решение



 -
оптимальное вырожденное решение.
-
оптимальное вырожденное решение.





 В стандартной форме
В стандартной форме 








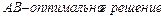
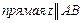
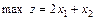 В стандартной форме
В стандартной форме 
 (1)
(1) 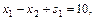
 (2)
(2) 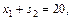
 (3)
(3) 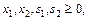
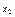


 - признак неограниченности решения. Присутствие отрицательного числа в результирующей строке признак неограниченности целевой функции.
- признак неограниченности решения. Присутствие отрицательного числа в результирующей строке признак неограниченности целевой функции.


 В стандартной форме
В стандартной форме 
 (1)
(1) 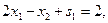
 (2)
(2) 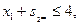
 (3)
(3) 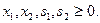
 (4)
(4)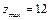


 ), обычно используются искусственные переменные, не гарантирующие получения допустимого решения в ее первоначальной подстановке. Несмотря на то, что используемые вычислительные процедуры должны привести к нулевым значениям искусственных переменных в оптимуме за счет введения штрафов,, этого удается добиться только тогда, когда допустимые решения существуют. В противном случае на итерации, приводящей к оптимуму, по крайней мере одна из искусственных переменных будет иметь положительное значение, а это свидетельствует о том, что ЗЛП не имеет допустимых решений.
), обычно используются искусственные переменные, не гарантирующие получения допустимого решения в ее первоначальной подстановке. Несмотря на то, что используемые вычислительные процедуры должны привести к нулевым значениям искусственных переменных в оптимуме за счет введения штрафов,, этого удается добиться только тогда, когда допустимые решения существуют. В противном случае на итерации, приводящей к оптимуму, по крайней мере одна из искусственных переменных будет иметь положительное значение, а это свидетельствует о том, что ЗЛП не имеет допустимых решений.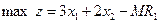

 (1)
(1) 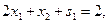
 (2)
(2) 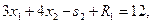
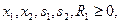


 свидетельствует об отсутствии решения
свидетельствует об отсутствии решения