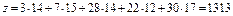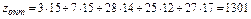Сбалансированная транспортная модель
Из представленной модели видно, что суммарный объём производства в исходных пунктах  не должен быть меньше суммарного спроса в пунктах назначения не должен быть меньше суммарного спроса в пунктах назначения  . .
Если суммарный объём производства равен суммарному спросу (  = =  ), то модель называется сбалансированной транспортной моделью. Она отличается от вышеприведённой модели лишь тем, что все ограничения превращаются в равенства, т.е. ), то модель называется сбалансированной транспортной моделью. Она отличается от вышеприведённой модели лишь тем, что все ограничения превращаются в равенства, т.е.
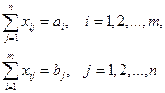
В реальных условиях не всегда объём производства равен спросу или превосходит его. Однако транспортную модель всегда можно сбалансировать. Так, например, если спрос превышает объём производства, можно ввести дополнительный фиктивный исходный пункт с производительностью недостающего объёма продукции. Поскольку на самом деле такого исходного пункта не существует, никакие перевозки не осуществляются, и соответствующая стоимость перевозки единицы продукции равна нулю.
Сбалансированную траспортную задачу удобно задавать в виде таблицы:
| Пункты
отправления
| Пункты назначения
| 
|  
| 
| 
| …
| 
| 
|

|

|

|
…
|

| 
| 
|

|

|

|
…
|

| 
| | …
| …
| …
| …
| …
| …
|
| 
|
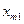
|

|

|
…
|

| 
| 
| 
| 
| 
| …
| 
|
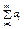  
|
 - количество продукции, производимой в пункте - количество продукции, производимой в пункте  ; ;
 - количество продукции, потребляемой в пункте - количество продукции, потребляемой в пункте 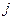 ; ;
 - количество продукции, перевозимой из пункта - количество продукции, перевозимой из пункта  в пункт в пункт 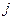 ; ;
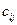 - стоимость перевозимой единицы продукции из пункта - стоимость перевозимой единицы продукции из пункта  в пункт в пункт 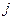 . .
Математическая запись сбалансированной ТЗ:
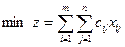
 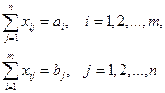
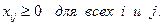
   - условие сбалансированности - условие сбалансированности
Задача 2. В ПО химчистки три цеха  выполняют заказы, поступающие с трех приёмных пунктов выполняют заказы, поступающие с трех приёмных пунктов 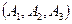 . Мощность цехов и пропускная способность приёмных пунктов ( в . Мощность цехов и пропускная способность приёмных пунктов ( в  ) составляют: пропускная способность приёмного пункта ) составляют: пропускная способность приёмного пункта  ; производственная мощность цеха ; производственная мощность цеха 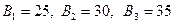 . Расстояние от каждого приёмного пункта до каждого цеха в . Расстояние от каждого приёмного пункта до каждого цеха в   . Требуется так организовать перевозку заказов с приёмных пунктов в цехи ПО, чтобы пропускная способность приёмных пунктов, прикреплённых к каждому цеху, в сумме не превышала бы мощности самого цеха; цехи полностью обеспечивали бы химчистку вещей для каждого приёмного пункта, и чтобы при этом общий объём перевозок в тонно-километрах был минимальным. . Требуется так организовать перевозку заказов с приёмных пунктов в цехи ПО, чтобы пропускная способность приёмных пунктов, прикреплённых к каждому цеху, в сумме не превышала бы мощности самого цеха; цехи полностью обеспечивали бы химчистку вещей для каждого приёмного пункта, и чтобы при этом общий объём перевозок в тонно-километрах был минимальным.
1. Математическая запись ТЗ:
а) Выбор неизвестных:  - объём перевозки груза из - объём перевозки груза из  в в  ( (  . .
б) Целевая функция  . .
в) Система ограничений:     = 90 = 90
Табличная запись ТЗ:
2 Решение транспортной задачи:
а) Составление опорного плана (метод наименьшей стоимости).
Из требования  = =  следует, что одно уравнение оказывается зависимым, т.е. транспортная модель содержит только следует, что одно уравнение оказывается зависимым, т.е. транспортная модель содержит только 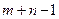 независимых уравнений. Таким образом начальное базовое допустимое решение должно иметь независимых уравнений. Таким образом начальное базовое допустимое решение должно иметь 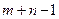 базисную переменную. Для получения этого решения используют метод наименьшей стоимости, правило северо-западного угла и другие. По методу наименьшей стоимости сначала берут первый пункт производства продукции базисную переменную. Для получения этого решения используют метод наименьшей стоимости, правило северо-западного угла и другие. По методу наименьшей стоимости сначала берут первый пункт производства продукции  и в первую очередь удовлетворяют потребность в продукции те пункты назначения, у которых затраты на перевозку единицы продукции и в первую очередь удовлетворяют потребность в продукции те пункты назначения, у которых затраты на перевозку единицы продукции  будут меньшими по сравнению с остальными, затем переходят к будут меньшими по сравнению с остальными, затем переходят к  и т.д. и т.д.
Вычислим значение целевой функции при таких допустимых значениях
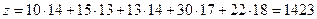
б) Проверка плана на оптимальность ( метод потенциалов ).
Для проверки опорного плана на оптимальность используют так называемый «метод потенциалов», по которому строке  и столбцу и столбцу 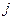 транспортной таблицы ставится в соответствие числа транспортной таблицы ставится в соответствие числа  и и  . Для каждой базисной переменной . Для каждой базисной переменной  текущего решения потенциалы текущего решения потенциалы  и и  должны удовлетворять уравнению должны удовлетворять уравнению  . Эти уравнения приводят к системе, состоящей из . Эти уравнения приводят к системе, состоящей из 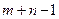 уравнений, в которых фигурируют уравнений, в которых фигурируют  неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из них произвольное значение ( обычно полагают неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из них произвольное значение ( обычно полагают 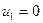 ). Как только решение получено, оценки для небазисных переменных ). Как только решение получено, оценки для небазисных переменных  определяются в соответствии с соотношением определяются в соответствии с соотношением  . Если в результате получатся отрицательные значения, то план считается не оптимальным, и его надо перестроить путем перераспределения продукции. . Если в результате получатся отрицательные значения, то план считается не оптимальным, и его надо перестроить путем перераспределения продукции.
Таким образом, для проверки опорного плана на оптимальность нужно проверить выполнение следующих двух правил:
1.  , ,
2.  . .
В нашем случае
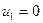
1.  2. 2. 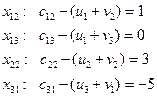
в) Улучшение опорного плана
После этого для включения в базис выбирается небазисная переменная, имеющая самую большую по модулю отрицательную оценку. В нашем случае это переменная  , для которой второе условие не выполняется. Для этой переменной строят многоугольник по указанной схеме, вершинам которого приписывают чередующиеся знаки, начиная со знака (+) для вводимой в базис переменной. Затем в вершинах со знаком (-) отыскивают наименьшую продукцию, которую и перемещают по вершинам многоугольника согласно знакам. , для которой второе условие не выполняется. Для этой переменной строят многоугольник по указанной схеме, вершинам которого приписывают чередующиеся знаки, начиная со знака (+) для вводимой в базис переменной. Затем в вершинах со знаком (-) отыскивают наименьшую продукцию, которую и перемещают по вершинам многоугольника согласно знакам.
  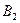 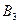  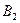 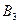

  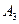   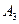
  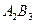  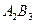
 - + - +
+ -
 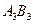  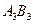
Этот цикл повторяется до тех пор, пока не будет выполняться второе условие для всех небазисных переменных.
Покажем оформление цикла на практике:
Первый цикл Второй цикл
      : 1 В1 В2 В3 А1В2: -4 В1 В2 В3 : 1 В1 В2 В3 А1В2: -4 В1 В2 В3
        0 А1В3: -5 0 А1В3: -5
 3 А2В1: 5 3 А2В1: 5
 -5 А1 А2 А3 А2В2: 3 А1 А2 А3 -5 А1 А2 А3 А2В2: 3 А1 А2 А3
 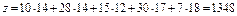
Третий цикл Четвертый цикл
      А1В2: -4 В1 В2 В3 А1В1: 4 А1В2: -4 В1 В2 В3 А1В1: 4
А2В1: 0 А2В1: 4
А2В2: -2 А2В2: 2
А3В3: 5 А1 А2 А3 А3В3: 1
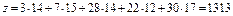 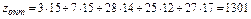
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 не должен быть меньше суммарного спроса в пунктах назначения
не должен быть меньше суммарного спроса в пунктах назначения  .
.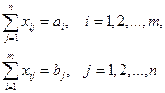



















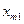









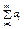


 ;
;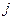 ;
; - количество продукции, перевозимой из пункта
- количество продукции, перевозимой из пункта 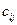 - стоимость перевозимой единицы продукции из пункта
- стоимость перевозимой единицы продукции из пункта 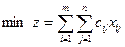

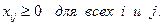

 выполняют заказы, поступающие с трех приёмных пунктов
выполняют заказы, поступающие с трех приёмных пунктов 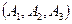 . Мощность цехов и пропускная способность приёмных пунктов ( в
. Мощность цехов и пропускная способность приёмных пунктов ( в  ) составляют: пропускная способность приёмного пункта
) составляют: пропускная способность приёмного пункта  ; производственная мощность цеха
; производственная мощность цеха 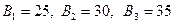 . Расстояние от каждого приёмного пункта до каждого цеха в
. Расстояние от каждого приёмного пункта до каждого цеха в 
 . Требуется так организовать перевозку заказов с приёмных пунктов в цехи ПО, чтобы пропускная способность приёмных пунктов, прикреплённых к каждому цеху, в сумме не превышала бы мощности самого цеха; цехи полностью обеспечивали бы химчистку вещей для каждого приёмного пункта, и чтобы при этом общий объём перевозок в тонно-километрах был минимальным.
. Требуется так организовать перевозку заказов с приёмных пунктов в цехи ПО, чтобы пропускная способность приёмных пунктов, прикреплённых к каждому цеху, в сумме не превышала бы мощности самого цеха; цехи полностью обеспечивали бы химчистку вещей для каждого приёмного пункта, и чтобы при этом общий объём перевозок в тонно-километрах был минимальным. в
в  (
(  .
. .
.

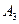




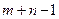 независимых уравнений. Таким образом начальное базовое допустимое решение должно иметь
независимых уравнений. Таким образом начальное базовое допустимое решение должно иметь  и в первую очередь удовлетворяют потребность в продукции те пункты назначения, у которых затраты на перевозку единицы продукции
и в первую очередь удовлетворяют потребность в продукции те пункты назначения, у которых затраты на перевозку единицы продукции  будут меньшими по сравнению с остальными, затем переходят к
будут меньшими по сравнению с остальными, затем переходят к  и т.д.
и т.д.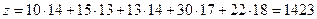
 и
и  . Для каждой базисной переменной
. Для каждой базисной переменной  . Эти уравнения приводят к системе, состоящей из
. Эти уравнения приводят к системе, состоящей из  неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из них произвольное значение ( обычно полагают
неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из них произвольное значение ( обычно полагают 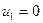 ). Как только решение получено, оценки для небазисных переменных
). Как только решение получено, оценки для небазисных переменных  определяются в соответствии с соотношением
определяются в соответствии с соотношением  . Если в результате получатся отрицательные значения, то план считается не оптимальным, и его надо перестроить путем перераспределения продукции.
. Если в результате получатся отрицательные значения, то план считается не оптимальным, и его надо перестроить путем перераспределения продукции. ,
, .
. 2.
2. 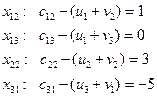







 - +
- +
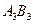

 10
10

 15
15 13
13

 10
10





 : 1 В1 В2 В3 А1В2: -4 В1 В2 В3
: 1 В1 В2 В3 А1В2: -4 В1 В2 В3






 0 А1В3: -5
0 А1В3: -5 3 А2В1: 5
3 А2В1: 5 -5 А1 А2 А3 А2В2: 3 А1 А2 А3
-5 А1 А2 А3 А2В2: 3 А1 А2 А3
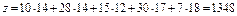

 3
3 22
22




 А1В2: -4 В1 В2 В3 А1В1: 4
А1В2: -4 В1 В2 В3 А1В1: 4