
|
|
Построение математической моделиФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Филиал государственного образовательного учреждения высшего Профессионального образования «Уфимский государственный нефтяной Технический университет» в г. Салавате КУРС ЛЕКЦИИ ПО РАЗДЕЛУ МАТЕМАТИКИ «ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ» Составитель: Ишемгулов А.Ф., ассистент Салават 2008 Линейное программирование
Задача линейного программирования Многие важные задачи экономики и планирования народного хозяйства, управления промышленностью тесно связаны с отысканием оптимального плана использования ограниченных ресурсов. Необходимость решения таких задач привела к широкому применению математических методов в экономике и планировании народного хозяйства и появлению нового раздела математики – математического программирования. В настоящее время завершена наиболее основательно часть этого нового раздела – линейного программирования. Задача линейного программирования (ЗЛП) состоит в отыскании оптимального значения заданной линейной функции при условии, что на переменные Линейная функция Z, оптимальное значение которой отыскивается в ЗЛП, называется целевой функцией, или функцией цели. Совокупность значений переменных Набор значений Из теории экстремума функции многих переменных известно, что оптимальное значение функция нескольких переменных достигает или на границе области её определения, или внутри области определения, а именно, в одной из точек экстремума. Известно также, что необходимым условием экстремума функции многих переменных является обращение в нуль всех её частных производных во внутренней точке области определения. Но частные производные Таким образом, рассматриваемая задача не может быть решена с помощью теории экстремума функции многих переменных, для решения её требуется применение особых математических приёмов, называемых методами линейного программирования.
Стандартная (каноническая) форма задачи линейного программирования В практических задачах формы линейных условий, определяющих многогранник решений ЗЛП, могут быть очень разнообразны. Часть условий может быть задана в виде равенств, причем на некоторые переменные могут не налагаться требования неотрицательности. Это затрудняет исследование ЗЛП и главное – требует разработки специальных методов для решения каждого варианта задачи. Поэтому возникает необходимость ввести понятие стандартной формы ЗЛП. При стандартной форме линейной модели а) все ограничения записываются в виде равенств с неотрицательной правой частью; б) значения всех переменных модели неотрицательны; в) целевая функция подлежит максимизации или минимизации. Покажем, каким образом любую линейную модель можно привести к стандартной.
Ограничения 1. Исходное ограничение, записанное в виде неравенства типа Например, в левую часть исходного ограничения 2. Рассмотрим исходное ограничение другого типа: 3. Правую часть равенства всегда можно сделать неотрицательной, умножая обе части на -1. Например, неравенство
Переменные Любую переменную
Целевая функция Целевая функция линейной оптимизационной модели, представленной в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Например, максимизация функции
Пример 1. Представить линейную модель в стандартной форме: min при ограничениях
Необходимо осуществить следующие преобразования:
а) умножить второе ограничение на -1 и вычесть из его левой части избыточную переменную
б) прибавить остаточную переменную в) в целевой функции и во всех ограничениях осуществить подстановку
Указанные операции позволяют привести исходную модель к стандартной форме: min при ограничениях Построение математической модели Процесс построения математической модели для решения поставленной задачи можно начать с ответов на три следующие вопроса: 1. Для определения каких величин должна быть построена модель? Другими словами, надо ввести переменные для решения задачи. 2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы? 3. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному решению задачи?
Задача 1. Фабрика изготовляет два вида красок: для внутренних (В) и наружных (Н) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта – А и С. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и С на 1 т соответствующих красок приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на краску (В) никогда не превышает спроса на краске (Н) более чем на 1 т. Кроме того, установлено, что спрос на краску (Н) никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. долл для краски (Н), 2 тыс. долл для краски (В). Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Переменные:
Целевая функция:
Ограничения:
Неявное ограничение заключается в том, что объёмы производства продукции не могут принимать отрицательных значений. Чтобы предотвратить получение таких недопустимых решений, потребуем выполнения условия неотрицательности переменных, т.е. введем ограничения на их знак:
Математическая модель данной задачи будет иметь вид:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ( 1)
( 1) наложены ограничения в виде линейных равенств или неравенств:
наложены ограничения в виде линейных равенств или неравенств: ( 2 )
( 2 ) линейной функции
линейной функции  нигде в области её определения одновременно в нуль не обращаются, следовательно, оптимальное значение функция Z может принимать только на границе области.
нигде в области её определения одновременно в нуль не обращаются, следовательно, оптимальное значение функция Z может принимать только на границе области. , можно представить в виде равенства, прибавляя остаточнуюпеременную к левой части ограничения (вычитаяизбыточнуюпеременную из левой части).
, можно представить в виде равенства, прибавляя остаточнуюпеременную к левой части ограничения (вычитаяизбыточнуюпеременную из левой части). вводится остаточная переменная
вводится остаточная переменная  , в результате чего исходное неравенство обращается в равенство
, в результате чего исходное неравенство обращается в равенство  .
.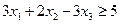 . Для обращения исходного неравенства в равенство, вычтем из его левой части избыточную переменную
. Для обращения исходного неравенства в равенство, вычтем из его левой части избыточную переменную  . В результате получим
. В результате получим  .
. заменить
заменить  .
. , не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных:
, не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных:  .
. эквивалентна минимизации функции
эквивалентна минимизации функции  . Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных
. Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных  в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.
в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.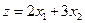

 ;
; к левой части третьего ограничения;
к левой части третьего ограничения; , т.к. в условии задачи
, т.к. в условии задачи  не имеет ограничения в знаке.
не имеет ограничения в знаке.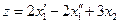
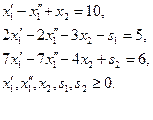
 - суточный объём производства краски (Н) (в тоннах)
- суточный объём производства краски (Н) (в тоннах) - суточный объём производства краски (В) (в тоннах)
- суточный объём производства краски (В) (в тоннах)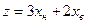
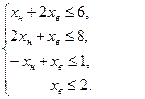
 (объём производства краски (В)),
(объём производства краски (В)), (объём производства краски (Н)).
(объём производства краски (Н)).
