Линейные комбинации двух векторов
Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Доказательство. 1) Необходимость. Пусть векторы  линейно зависимы. Докажем их коллинеарность. линейно зависимы. Докажем их коллинеарность.
По определению линейной зависимости найдутся такие вещественные числа a и b, хотя бы одно из которых не равно нулю, что справедливо равенство
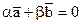 . .
Пусть b¹0. Тогда  . .
Обозначив 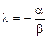 , получим , получим 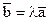 . .
Необходимость доказана.
2). Достаточность. Пусть векторы  коллинеарны. Докажем, что они линейно зависимы. Если хотя бы один из них нулевой, то коллинеарны. Докажем, что они линейно зависимы. Если хотя бы один из них нулевой, то  линейно зависимы. линейно зависимы.
Если же вектор  ненулевой, то из коллинеарности векторов ненулевой, то из коллинеарности векторов  следует, что следует, что 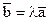 , т.е. , т.е.  , ч.т.д. , ч.т.д.
Следствие 1.Если векторы  не коллинеарны, то они линейно независимы. не коллинеарны, то они линейно независимы.
Следствие 2. Среди двух неколлинеарных векторов не может быть нулевого вектора.
Линейные комбинации трех векторов
Определение.Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.
Теорема.Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.
Доказательство.1). Необходимость. Пусть три вектора  линейно зависимы. Докажем их компланарность. линейно зависимы. Докажем их компланарность.
По определению линейной зависимости найдутся такие вещественные числа a, b и g, хотя бы одно из которых отлично от нуля, что
 . .
Пусть g¹0. Тогда
 . .
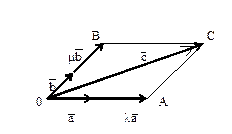 Обозначив l= - Обозначив l= -  , m= - , m= - 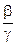 , имеем , имеем 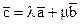 . Если все три вектора приложены к общему началу О, то отсюда следует, что вектор . Если все три вектора приложены к общему началу О, то отсюда следует, что вектор  равен диагонали параллелограмма, построенного на векторах равен диагонали параллелограмма, построенного на векторах  (рис.4) (рис.4)
Рис. 1
Но это означает, что векторы  лежат в одной плоскости, т.е. компланарны. лежат в одной плоскости, т.е. компланарны. 
2). Достаточность. Пусть векторы 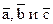 компланарны. Докажем, что они линейно зависимы. компланарны. Докажем, что они линейно зависимы.
Если какая-нибудь пара из указанных трех векторов коллинеарна, то эта пара линейно зависима и все три вектора  линейно зависимы. линейно зависимы.
Осталось рассмотреть случай, когда в тройке векторов  ни одна пара векторов не коллинеарна. ни одна пара векторов не коллинеарна.
Перенесем три компланарных вектора  на одну плоскость и приведем их к общему началу О (рис.1). Через конец C вектора на одну плоскость и приведем их к общему началу О (рис.1). Через конец C вектора  проведем прямые, параллельные векторам проведем прямые, параллельные векторам  . Обозначим А точку пересечения прямой, параллельной вектору . Обозначим А точку пересечения прямой, параллельной вектору 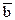 , с прямой, на которой лежит вектор , с прямой, на которой лежит вектор  , а В-точку пересечения прямой, параллельной вектору , а В-точку пересечения прямой, параллельной вектору  ,с прямой, на которой лежит вектор ,с прямой, на которой лежит вектор 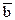 . (Точка пересечения существует, т.к. векторы . (Точка пересечения существует, т.к. векторы  не коллинеарны.) не коллинеарны.)
 . .
Так как вектор  коллинеарен ненулевому вектору коллинеарен ненулевому вектору  , то , то
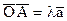 . .
Аналогично 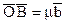 , т.е. , т.е. 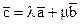 . .
Или 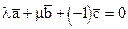 , ч.т.д. , ч.т.д.
Следствие 1.Каковы бы ни были неколлинеарные векторы  , для любого вектора , для любого вектора  , лежащего в одной плоскости с векторами , лежащего в одной плоскости с векторами  , найдутся такие вещественные числа l и m, что , найдутся такие вещественные числа l и m, что
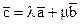 . .
Следствие 2. Если векторы`а,`в и`с не компланарны, то они линейно независимы.
Понятие базиса. Аффинные координаты
Определение 1.Три линейно независимых вектора 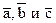 образуют в пространстве базис, если любой вектор образуют в пространстве базис, если любой вектор  может быть представлен в виде линейной комбинации векторов может быть представлен в виде линейной комбинации векторов 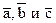 . .
Аналогично определяется базис на плоскости p.
Определение 2.Два лежащих в плоскости p линейно независимых вектора  образуют на этой плоскости базис, если любой лежащий в этой плоскости вектор образуют на этой плоскости базис, если любой лежащий в этой плоскости вектор  может быть представлен в виде линейной комбинации векторов может быть представлен в виде линейной комбинации векторов  . .
Имеют место следующие фундаментальные утверждения:
1) любая тройка некомпланарных векторов 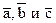 образует базис в пространстве; образует базис в пространстве;
2) любая пара лежащих в данной плоскости неколлинеарных векторов  образует базис на этой плоскости. образует базис на этой плоскости.
Теорема. Каждый вектор  может быть единственным способом разложен по базису может быть единственным способом разложен по базису  : :
 . .
Числа l, m, g называются координатами вектора  относительно базиса относительно базиса  . .
Теорема.При сложении двух векторов 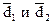 их координаты складываются. При умножении вектора их координаты складываются. При умножении вектора  на любое число a все его координаты умножаются на это число. на любое число a все его координаты умножаются на это число.
Аффинные координаты в пространстве определяются заданием базиса  и некоторой точки О, называемой началом координат. и некоторой точки О, называемой началом координат.
Аффинными координатами любой точки М называются координаты вектора 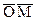 (относительно базиса (относительно базиса  ). ).
Свойства базиса и понятие аффинных координат на плоскости аналогичны случаю пространства.
Проекция вектора на ось
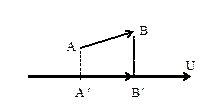 Определение.Проекцией вектора Определение.Проекцией вектора 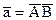 на ось U называется величина на ось U называется величина  направленного отрезка направленного отрезка 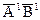 оси U, где оси U, где  - основания перпендикуляров, опущенных на ось U из точек A и B соответственно(рис.10). - основания перпендикуляров, опущенных на ось U из точек A и B соответственно(рис.10).
ТеоремаПроекция вектора  на ось U равна длине вектора на ось U равна длине вектора  , умноженной на косинус j угла наклона вектора , умноженной на косинус j угла наклона вектора  к оси U. к оси U.
Доказательство.

|
Обозначим через V ось, проходящую через начало A вектора  и имеющую тоже направление, что и ось U, и пусть C- проекция B на ось V. и имеющую тоже направление, что и ось U, и пусть C- проекция B на ось V.
| ÐBAC=j,  = AC. = AC.
Так как по определению при 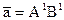 , то при , то при  . .
Но  cosj= cosj=  cosj. Следовательно при cosj. Следовательно при 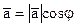 и т.д. и т.д.
Декартова прямоугольная система координат (ДПСК)
в пространстве.
ДПСК является частным случаем аффинной системы, отвечающим тройке взаимно ортогональных и единичных базисных векторов  . Принято направления векторов . Принято направления векторов  брать совпадающими с направлением декартовых осей Ox, Oy, Oz соответственно. брать совпадающими с направлением декартовых осей Ox, Oy, Oz соответственно.
Нами получено, что любой вектор  может быть, причем единственным способом, разложен по декартову прямоугольному базису (ДПБ) может быть, причем единственным способом, разложен по декартову прямоугольному базису (ДПБ)  , т.е. для каждого вектора , т.е. для каждого вектора  существует единственная тройка чисел X, Y, Z такая, что существует единственная тройка чисел X, Y, Z такая, что
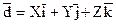 . (1) . (1)
Числа X, Y, Z называются декартовыми прямоугольными координатами (ДПК) вектора  . Если M- любая точка пространства, то ДПК этой точки совпадают с ДПК вектора . Если M- любая точка пространства, то ДПК этой точки совпадают с ДПК вектора 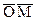 . .
Вектор 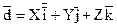 будем также записывать в виде будем также записывать в виде  . .
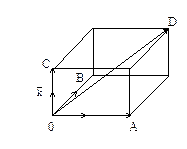
Теорема.ДПК вектора  равны проекциям этого вектора на оси OX, OY и OZ соответственно. равны проекциям этого вектора на оси OX, OY и OZ соответственно.
Доказательство.
|
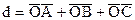 . .
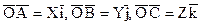
 , т.к. из , т.к. из  и того, что и того, что  ,
получаем ,
получаем 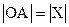 .
Но знаки OA и X совпадают, .
Но знаки OA и X совпадают,
| так как. когда векторы  направлены в одну сторону , оба числа OA и X положительны, а в случае, когда векторы направлены в одну сторону , оба числа OA и X положительны, а в случае, когда векторы  направлены в противоположные стороны, оба числа OA и X отрицательны. Т.е. OA=X. направлены в противоположные стороны, оба числа OA и X отрицательны. Т.е. OA=X.
Аналогично OB=Y, OC=Z, ч.т.д.
Обозначим a, b, g углы наклона вектора  к осям Ox, Oy, Oz соответственно. Числа cosa, cosb, cosg называют направляющими косинусами вектора к осям Ox, Oy, Oz соответственно. Числа cosa, cosb, cosg называют направляющими косинусами вектора  . .
Из теорем имеем
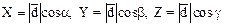 (2) (2)
Т.к. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то из равенств OA=X, OB=Y, OC=Z получим выражение для длины вектора  через его координаты: через его координаты:
 (3) (3)
Из формул (1) и (2) имеем:
 , , 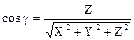 . .
Возводя в квадрат и складывая последние равенства, получим

Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 линейно зависимы. Докажем их коллинеарность.
линейно зависимы. Докажем их коллинеарность.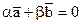 .
. .
.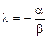 , получим
, получим 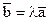 .
. ненулевой, то из коллинеарности векторов
ненулевой, то из коллинеарности векторов  , ч.т.д.
, ч.т.д. не коллинеарны, то они линейно независимы.
не коллинеарны, то они линейно независимы. линейно зависимы. Докажем их компланарность.
линейно зависимы. Докажем их компланарность. .
. .
.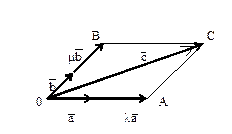 Обозначив l= -
Обозначив l= -  , m= -
, m= - 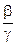 , имеем
, имеем 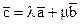 . Если все три вектора приложены к общему началу О, то отсюда следует, что вектор
. Если все три вектора приложены к общему началу О, то отсюда следует, что вектор  равен диагонали параллелограмма, построенного на векторах
равен диагонали параллелограмма, построенного на векторах  (рис.4)
(рис.4)
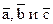 компланарны. Докажем, что они линейно зависимы.
компланарны. Докажем, что они линейно зависимы. линейно зависимы.
линейно зависимы.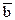 , с прямой, на которой лежит вектор
, с прямой, на которой лежит вектор  .
. коллинеарен ненулевому вектору
коллинеарен ненулевому вектору 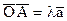 .
.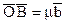 , т.е.
, т.е. 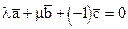 , ч.т.д.
, ч.т.д.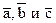 образуют в пространстве базис, если любой вектор
образуют в пространстве базис, если любой вектор  может быть представлен в виде линейной комбинации векторов
может быть представлен в виде линейной комбинации векторов  :
: .
.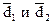 их координаты складываются. При умножении вектора
их координаты складываются. При умножении вектора  на любое число a все его координаты умножаются на это число.
на любое число a все его координаты умножаются на это число.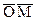 (относительно базиса
(относительно базиса 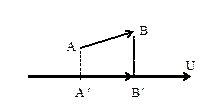 Определение.Проекцией вектора
Определение.Проекцией вектора 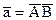 на ось U называется величина
на ось U называется величина  направленного отрезка
направленного отрезка 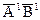 оси U, где
оси U, где  - основания перпендикуляров, опущенных на ось U из точек A и B соответственно(рис.10).
- основания перпендикуляров, опущенных на ось U из точек A и B соответственно(рис.10).
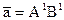 , то при
, то при  .
. cosj=
cosj=  cosj. Следовательно при
cosj. Следовательно при 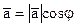 и т.д.
и т.д. . Принято направления векторов
. Принято направления векторов 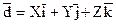 . (1)
. (1)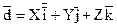 будем также записывать в виде
будем также записывать в виде  .
.
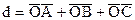 .
.
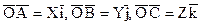
 , т.к. из
, т.к. из  и того, что
и того, что  ,
получаем
,
получаем 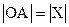 .
Но знаки OA и X совпадают,
.
Но знаки OA и X совпадают,
 направлены в одну сторону , оба числа OA и X положительны, а в случае, когда векторы
направлены в одну сторону , оба числа OA и X положительны, а в случае, когда векторы 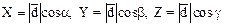 (2)
(2) (3)
(3) ,
, 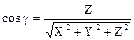 .
.