
|
|
Матрицы. Основные определенияМатрицей А=(
Числа Если m=n, то матрица называется квадратной порядка n. Например, Треугольная матрица – квадратная матрица, у которой все элементы, стоящие по одну из сторон главной диагонали, равны нулю:
Квадратная матрица вида
называется диагональной матрицей. Если
Симметрической называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны, т.е. Например, Матрица, состоящая из одной строки, называется вектором-строкой, а матрица, состоящая из одного столбца, – вектором-столбцом. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается О. Например, О
Действия над матрицами Две матрицы Суммой двух матриц
Для суммы матриц справедливы следующие свойства: 1. A+B=B+A – коммутативность; 2. A+(B+C)=(A+B)+C – ассоциативность; 3. A+О=A. Произведением матрицы Пусть A, B, C – матрицы, 1. 2. 3. Матрица Если матрицы A и B одинаковых размеров, то их разность равна Произведением матрицы
Из определения произведения матриц следует: чтобы получить элемент, стоящий на пересечении i-й строки и j-го столбца матрицы С, необходимо элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить. Произведение АВ имеет смысл тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В. В результате получится матрица, у которой число строк совпадает с числом строк первого сомножителя, а число столбцов – Для произведения матриц справедливы следующие свойства:
Эти свойства легко доказываются на основе соответствующих определений. Произведение двух матриц некоммутативно, т.е. в общем случае АВ Пример. Найти произведение АВ и ВА матриц: А = Решение.
Пример. Найти произведение матриц А и В.
Решение:
Если АВ=ВА, то матрицы А и В называются коммутативными. Так, например, единичная матрица Е коммутативна с любой квадратной матрицей того же порядка, причем АЕ=ЕА=А. Квадратную матрицу А можно возвести в степень n, для чего ее надо умножить на саму себя n раз, т.е. Транспонирование матрицы – это такое преобразование, при котором строки заменяются соответствующими столбцами:
Транспонированная матрица обладает следующими свойствами, которые следуют из определения: 1. (А 2. (А+В) 3. (AB) Если матрица А – симметрическая, то А Очевидно, что произведение С=АА С При этом А может быть и прямоугольной матрицей произвольного порядка, С же будет квадратной, порядка, соответствующего числу строк матрицы А. Обратная матрица Пусть задана квадратная матрица Определение. Квадратная матрица А-1 порядка n называется обратной к матрице А, если она удовлетворяет соотношению
Присоединенной матрицей квадратной матрицы А называется матрица А*, каждый элемент
Квадратная матрица А называется невырожденной (неособенной), если ее определитель |A| отличен от нуля, и вырожденной, если |A|=0. Теорема. Для всякой невырожденной матрицы А существует единственная обратная матрица А-1, определяемая следующим выражением:
Обратная матрица обладает следующими основными свойствами: 1. Определитель обратной матрицы равен обратной величине определителя исходной матрицы, т.е. |A-1|= 2. Произведение двух невырожденных матриц А и В является невырожденной матрицей и 3. Если матрица А невырожденная, то 4. Обратная матрица к транспонированной является транспонированной матрицей к обратной, т.е.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 )
)  называется прямоугольная таблица чисел, содержащая m строк и n столбцов:
называется прямоугольная таблица чисел, содержащая m строк и n столбцов: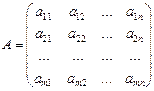
 ), составляющие данную матрицу, называются её элементами; i – номер строки матрицы, j – номер столбца.
), составляющие данную матрицу, называются её элементами; i – номер строки матрицы, j – номер столбца. – квадратная матрица третьего порядка. Про элементы
– квадратная матрица третьего порядка. Про элементы  такой матрицы говорят, что они стоят на главной диагонали.
такой матрицы говорят, что они стоят на главной диагонали. , например,
, например,  – треугольная матрица третьего порядка
– треугольная матрица третьего порядка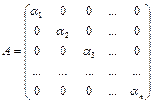

 , то матрица называется единичной и обозначается буквой Е, т.е.
, то матрица называется единичной и обозначается буквой Е, т.е. .
.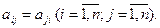
 – симметрическая матрица четвертого порядка.
– симметрическая матрица четвертого порядка. -нулевая матрица размера два на три.
-нулевая матрица размера два на три. и
и 
 ,
, 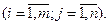
 называется матрица C=A+B, элементы которой сij равны сумме соответствующих элементов aij и bij матриц A и B, т.е.
называется матрица C=A+B, элементы которой сij равны сумме соответствующих элементов aij и bij матриц A и B, т.е.  . Например,
. Например, ,
, 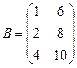 ,
,  .
. на число
на число  называется матрица
называется матрица  , элементы которой равны произведению соответствующих элементов матрицы A на число
, элементы которой равны произведению соответствующих элементов матрицы A на число  . Например, если
. Например, если  , а матрица
, а матрица  , то
, то  .
. – числа. Из определения произведения матрицы на число вытекают следующие свойства:
– числа. Из определения произведения матрицы на число вытекают следующие свойства: , 4.
, 4.  ,
, , 5.
, 5.  ,
, О, 6.
О, 6.  .
. называется противоположной матрице A.
называется противоположной матрице A. .
. порядка
порядка  на матрицу
на матрицу  порядка
порядка 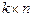 называется матрица
называется матрица  порядка
порядка  , элементы которой с
, элементы которой с  равны:
равны: , (
, (  ;
;  ).
). ВА. В случае прямоугольных матриц легко подобрать примеры, когда одно из этих произведений не будет существовать из-за невыполнения условия равенства числа столбцов сомножителя, стоящего первым, числу строк второго сомножителя. Очевидно, что для квадратных матриц порядка n существуют АВ и ВА. Однако для всех n, начиная с n=2, можно привести примеры некоммутативных (неперестановочных) матриц.
ВА. В случае прямоугольных матриц легко подобрать примеры, когда одно из этих произведений не будет существовать из-за невыполнения условия равенства числа столбцов сомножителя, стоящего первым, числу строк второго сомножителя. Очевидно, что для квадратных матриц порядка n существуют АВ и ВА. Однако для всех n, начиная с n=2, можно привести примеры некоммутативных (неперестановочных) матриц. , В =
, В =  .
. ;
;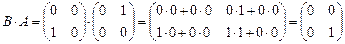
 ,
,  .
.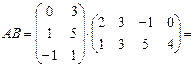
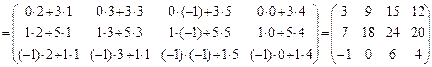
 .
.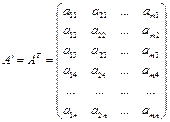
 )
)  порядка n.
порядка n. .
.
 которой есть алгебраическое дополнение элемента
которой есть алгебраическое дополнение элемента  .
.
 .
. .
. .
. .
.