
|
|
Методы решения системы n линейных уравнений с n неизвестнымиРассмотрим систему n линейных уравнений с n неизвестными
Определитель |A| матрицы А называется определителем системы (1). Теорема Крамера. Если определитель |A| системы (1) отличен от нуля, то система совместна и имеет единственное решение.
Из формулы (2) следует, что если система (1) совместна, то она обладает единственным решением. Формулы (2) называются формулами Крамера. Непосредственной подстановкой значений
При Таким образом, получим
Пример. Решить систему линейных уравнений методом Крамера:
Решение. Вычислим определитель
откуда Решение системы линейных уравнений с определителем |A|, отличным от нуля, можно найти с помощью обратной матрицы. Для этого запишем систему (1) в виде матричного уравнения
где Решение матричного уравнения (4) имеет вид
Пример. Решить систему линейных уравнений с помощью обратной матрицы
Решение. Вычислим для матрицы
ее обратную матрицу
Определим неизвестную матрицу-столбец Х:
откуда Формулы Крамера (3) могут быть получены из выражения (5). Действительно, запишем матричное равенство
Из полученного выражения непосредственно следуют формулы Крамера:
Методы решения системы m линейных уравнений Рассмотрим решение системы m линейных уравнений с n переменными в общем виде:
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Предположим, что в системе (6) коэффициент при первой переменной x1 в первом уравнении a11≠0 ( если это не так, то перестановкой уравнений местами добьемся того, что a11≠0). Шаг 1. Умножая первое уравнение на подходящие числа (а именно на -a21/a11, - a31/a11,…., -am1/a11) и прибавляя полученные уравнения соответственно ко второму, третьему,….., m –му уравнению системы (1), исключим переменную x1 из всех последующих уравнений, начиная со второго. Получим:
Где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага. Шаг 2. Предположим, что a(1)22≠0 ( если это не так, то соответствующей перестановкой уравнений или переменных с изменением их номеров добьемся того, чтобы a(1)22≠0). Умножая второе уравнение на подходящие числа (-a(1)32/a(1)22, -a(1)42/a(1)22,…, -a(1)m2/a(1)22) и прибавляя полученные уравнения соответственно к третьему, четвертому,….., m- му уравнению системы, исключим переменную x2 из всех последующих уравнений, начиная с третьего. Продолжая процесс последовательного исключения переменных x3,x4,…,xr-1, после (r-1) –го шага получим систему
Число нуль в последних m-r уравнениях означает, что их левые части имеют вид 0*x1+0*x2+….+0*xn. Если хотя бы одно из чисел Таким образом, для любой совместной системы числа Переход системы (6) к равносильной ей системе (8) называется прямым ходом метода Гаусса, а нахождение переменных из системы (8) – обратным ходом. Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу
называемую расширенной матрицей системы (6) , ибо в нее, кроме матрицы системы А, дополнительно включен столбец свободных членов. Пример. Решить систему уравнений:
Решение. Расширенная матрица системы имеет вид:
Шаг 1. Так как a11≠0, то, умножая первую строку на число (-2) и прибавляя соответственно ко второй и третьей, четвертой строкам, исключим переменную x1 из всех строк, начиная со второй. Заметив, что в новой матрице
Шаг 2. Так как теперь
Шаг 3. Учитывая, что
Откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения x4=-2; из третьего x1=6+2x4-3x3-2x2=6+2(-2)-3(-1)-2*2=1, т.е. решение системы (1;2;-1;2). Пример2. Методом Гаусса решить систему уравнений:
Решение. Преобразуем расширенную матрицу системы
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0=-1, следовательно данная система несовместна. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

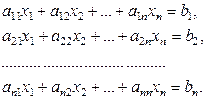

 , во все уравнения системы убедимся в том, что они образуют ее решение:
, во все уравнения системы убедимся в том, что они образуют ее решение: .
. ,
,  при
при  ,
,  .
. .
.
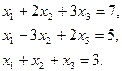
 :
: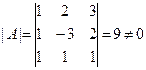
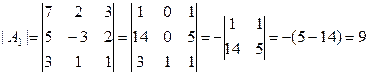 ,
, ,
, ,
,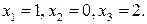
 .
.
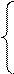
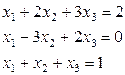
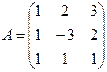
 .
. ,
,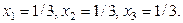

 .
. .
. (6)
(6) (7)
(7)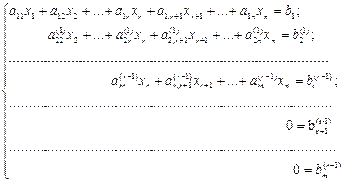 (8)
(8) не равно нулю, то соответствующее равенство противоречиво, и система (6) несовместна.
не равно нулю, то соответствующее равенство противоречиво, и система (6) несовместна. , (9)
, (9)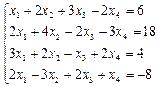
 .
. , поменяем местами вторую и третью строки:
, поменяем местами вторую и третью строки: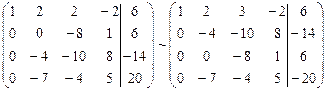 .
. , то, умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную x2 из всех строк, начиная с третьей:
, то, умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную x2 из всех строк, начиная с третьей: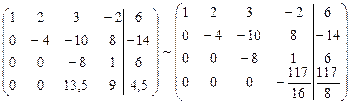
 , умножаем третью строку на 13,5/8=27/16 и, прибавляя полученную строку к четвертой, исключим из нее переменную x3. Получим систему уравнений:
, умножаем третью строку на 13,5/8=27/16 и, прибавляя полученную строку к четвертой, исключим из нее переменную x3. Получим систему уравнений: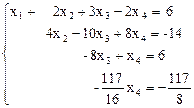
 ; из второго
; из второго  и из первого уравнения
и из первого уравнения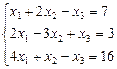
 .
.