|
|
Дизъюнктивная нормальная форма. Совершенная дизъюнктивная нормальная форма.Определение 2. Конъюнкция
называется элементарной конъюнкцией или конъюнктом. Так как существует всего 2n различных наборов значений переменной sÎ{0, 1}, то существует соответственно 2n различных элементарных конъюнкций от n переменных. При этом значение элементарной конъюнкции вида (4.1) равно 1 тогда и только тогда, когда xi=si для всех i=1, 2, …, n. Конъюнкция вида (4.1) называется также конституентой единицы. Определение 3. Дизъюнктивной нормальной формой формулыА (ДНФА) называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций. Пример 4.1. Для формулы А= Как видим из этого примера, ДНФ формулы, вообще говоря, неединствен. Вообще, их можно составить сколько угодно. Действительно, к ДНФ формулы можно прийти по следующему алгоритму: I шаг: Приведение операций |, ¯, ®, «, Å к операциям &, Ú или их отрицаниям: 1. Если в формуле участвуют операции |, ¯, и Å, то от них с помощью операции отрицания переходим к отрицанию соответственно конъюнкций, дизъюнкций или эквиваленций. 2. Если в формуле участвует операция «, то от неё с помощью закона т) упражнения 3.2 переходим к операции ®. 3. Если в формуле участвует операция ®, то от неё с помощью закона п) упражнения 3.2 преходим к операции Ú. II шаг. Отнесение отрицаний к пропозициональным переменным. 4. Если в формуле участвуют отрицания конъюнкций или дизъюнкций, то с помощью законов де Моргана отрицания приводим к пропозициональным переменным. 5. Если в формуле участвует двойное отрицание, то с помощью закона снятия двойного отрицания они убираются. III шаг. Получение ДНФ. С помощью свойства дистрибутивности & относительно Ú все подформулы вида A(B1ÚB2Ú…ÚBk) приводим к подформулам вида AB1ÚAB2Ú…ÚABk до тех пор, пока не получим дизъюнкцию элементарных конъюнкций. Таким образом, мы доказали, что любая формула эквивалентна некоторой ДНФ. Что касается того, что ДНФ формулы можно построить сколько угодно, то это становится очевидным, если увидеть, что АÚАÚ…ÚА~А, и поэтому в ДНФ элементарная конъюнкция может повторяться сколько угодно раз. В приведённом примере третья ДНФ отличается от первой и второй тем, что она удовлетворяет следующим четырём свойствам совершенства: 1. Каждый конъюнкт ДНФ формулы содержит все переменные или их отрицания, входящие в формулу. 2. Все конъюнкты, входящие в ДНФ, различны. 3. Ни один конъюнкт, из которых состоит ДНФ, не содержит одновременно переменную и её отрицание. 4. Ни один конъюнкт не содержит одну же литеру два и более раз. Определение 4. ДНФ формулы, удовлетворяющей всем условиям совершенства, называется совершенной дизъюнктивной нормальной формой данной формулы (СДНФ). Для того, чтобы получить СДНФ формулы А, достаточно сначала формулу привести к ДНФА, а затем применить к полученной ДНФ эквивалентные преобразования следующих видов, позволяющие последовательно получать эквивалентную ДНФА, удовлетворяющие всем условиям совершенства: 1. Если в ДНФА какой-либо конъюнкт В не содержит переменную хi или её отрицание, то используя равносильности B~В&(хiÚ 2. Если в ДНФА входят два или более одинаковых конъюнкта B, то лишние отбрасываем, пользуясь равносильностью BÚBÚ…ÚB~B. 3. Если некоторый конъюнкт В, входящий в ДНФА, содержит переменную хi и её отрицание 4. Если некоторый конъюнкт, входящий в ДНФА, содержит одну и ту же литеру Упражнение 4.1. С помощью эквивалентных преобразований привести формулы упражнения 3.4 к СДНФ. Решение. з) Приведём формулу к ДНФ: (x|
Получили ДНФ формулы. Теперь преобразуем ДНФ по алгоритму получения всех условий совершенства:
á(1) Одновременно заменили | на отрицание операции &, и ® - на отрицание Ú. (2) Одновременно применили закон двойного отрицания и Å заменили на « и его отрицание. (3) Операцию « заменили на ®. (4) Применили закон де Моргана. (5) Заменили ® на Ú. (6), (7) Одновременно применили законы де Моргана и снятия двойного отрицания. (8) Воспользовались дистрибутивностью & относительно Ú. (9) 1-й, 2-й и 3-й конъюнкты преобразовали, добавив недостающие переменные и их отрицания заменив каждый из них на два (шаг 1-й алгоритма приведения к СДНФ). (10) 5-й и 6-й конъюнкты опустили, так как они уже участвуют в полученной ДНФ (шаг 2-го алгоритма). СДНФ формулы существует и единственна. Существование СДНФ для любой формулы вытекает из алгоритма её построения. Другой способ построения СДНФА основывается на следующей эквиваленции: A(х1, х2, …, хn)~ Другими словами, формула A(х1, х2, …, хn) в своей СДНФ содержит те и только те конъюнкты вида (4.1), значения которых равны 1 при xi=si для всех i=1, 2, …, n. Например, для формулы А= Таким образом, СДНФA(х1, х2, …, хn)= Упражнение 4.2. С помощью таблиц истинности привести формулы упражнения 3.4 к СДНФ. Решение. д). 1. Составим таблицу истинности формулы:
2. Выберем те наборы значений переменных, при которых формула принимает значение 1: (0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). 3. Составим соответствующие им конъюнкты: 4. Составим из них ДНФ: Ответ: д) СДНФ A= 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
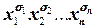 (4.1)
(4.1)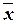 ®(
®( 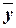 Ú
Ú 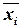 )~ ~(В&хi)Ú(B&
)~ ~(В&хi)Ú(B& 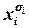 дважды или более, то, пользуясь равносильностью
дважды или более, то, пользуясь равносильностью  )®(zÅ
)®(zÅ  )
) 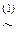 (
(  )Ú(zÅ
)Ú(zÅ  (x&
(x& 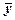 )Ú
)Ú 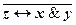
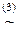
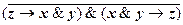
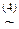 (x&
(x& 
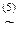
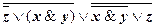
 (x&
(x& 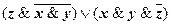
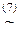
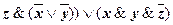
 (x&
(x& 
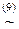
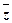 )Ú(
)Ú( 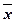 &y&z)Ú(
&y&z)Ú(  &
& 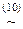
 .
.