
|
|
Булевы функции и основные их классы. Полином Жегалкина.
Целью данного параграфа является знакомство с основными объектами пособия - булевыми функциями. Напомним понятие функции. Согласно определения (см. часть I), отношение fÍA´B называется функцией (или отображением) из множества A в множество B, если df=A, rfÍB и из (х, y1)Îf, (х, y2)Îf следует y1=y2. Функция f из A в B обозначается через f: A®B или A Другими словами, функцией называется такое правило f, которое каждому элементу одного множества A ставит в соответствие однозначно определённый элемент другого множества B. 5.1. Понятие булевой функции и способы её задания. Определение 1. Булевой функцией называется любая функция f, область определения которой совпадает с декартовой n-й степенью множества {0, 1}, а область значений - с {0, 1}. Другими словами, f - булева функция, если df={0, 1}п, rf={0, 1}. Для булевой функции дадим ещё одно Определение 1¢. Булевой функцией называется любая функция f, которая произвольному набору (s1, s2, …, sn) из нулей и единиц ставит в соответствие значение f(s1, s2, …, sn)Î{0, 1}. Булевы функции также называют переключательными функциями. Мы видели, что любая формула алгебры логики ставит в соответствие произвольному набору (s1, s2, …, sn) из нулей и единиц некоторое однозначно определённое значение из множества {0, 1}. Поэтому, любую формулу алгебры логики можно рассматривать как некоторую функция. Но мы также видели, что существуют эквивалентные между собой формулы, которые имеют одинаковые таблицы истинности, и, тем самым, представляют одинаковые отображения из {0, 1}п на {0, 1}. Следовательно, эквивалентные между собой формулы можно рассматривать как одну и ту же булеву функцию. С другой стороны, если задана булева функция, то, естественно, нам известно, какому набору из нулей и единиц она ставит в соответствие 0 или 1, то есть нам известна таблица значений этой функции, которая, очевидно, имеет структуру таблицы истинности некоторой формулы. Так как для любой таблицы истинности мы можем построить некоторую формулу, то и для любой булевой функции мы можем построить её определяющую формулу. Тем самым, мы приходим к следующему определению. Определение 2. ФормулаFпредставляет функциюf, если их таблицы истинности совпадают. Таким образом, функцию можно задать с помощью формулы, представляющей её. Такой способ задания называется также аналитическим. Итак, любую булеву функцию можно рассматривать как некоторую формулу. Поэтому, все понятия и факты, связанные с формулами алгебры логики, рассмотренные нами выше, распространяются и на булевы функции. В частности, над булевыми функциями производятся логические операции В частности, на множестве Фп булевых функций от п переменных рассматривается булева алгебра áФп; &, Ú; Ø; 0, 1ñ. Она изоморфна фактор-алгебре Fn/~ булевой алгебры по конгруэнции ~ - отношения эквиваленции между формулами. Наконец, áФп; Å, &ñ - кольцо. Оно изоморфно фактор-кольцу булева кольца по той же конгруэнции. Дальнейшее изложение мы будем вести преимущественно относительно булевых функций. Преимуществ в этом можно указать целый ряд. Пока же укажем только тот факт, что от п переменных существует При составлении таблицы истинности наборы значений нулей и единиц располагаются в лексикографическом порядке. Поэтому, если указать в соответствующем порядке значения функции, то тем самым мы определим функцию. Определение 3. Вектором значений булевой функции f называется упорядоченный набор всех её значений, соответствующих лексикографическому порядку множества аргументов. Таким образом, функцию можно задать с помощью её вектора значений. Наконец, для задания функции достаточно указать, при каких наборах значений переменных функция принимает значение 1 либо, наоборот, 0. Другими словами, функцию можно задать с помощью системы равенств вида f(s1, s2, …, sn)=1 или системы равенств вида f(s1, s2, …, sn)=0. Пример 5.1. Функцию, заданную формулой (х®у)&(у®z)&(z®x), можно задать с помощью вектора значений (10101111), а также систем равенств f(0, 0, 0)=f(0, 1, 0)=f(1, 0, 0)=f(1, 0, 1)=f(1, 1, 0)=f(1, 1, 1)=1 либо f(0, 0, 1)=f(0, 1, 1)=0. Упражнение 5.1. Функция f(x, y, z) задана системой своих значений. Найти ДНФ и КНФ функции: а) f(0, 0, 1)=f(0, 1, 0)=f(1, 0, 1)=1; б) f(0, 0, 1)=f(0, 1, 1)=f(1, 1, 0)=f(1, 1, 1)=0; в) f(0, 0, 0)=f(0, 1, 0)=f(0, 1, 1)=f(1, 0, 1)=1. Решение. а) Нам даны те наборы значений переменных, при которых функция принимает значение 1: (0, 0, 1), (0, 1, 0), (1, 0, 1). Составим соответствующие им конъюнкты: На остальных наборах (0, 0, 0), (0, 1, 1), (1, 0, 0), (1, 1, 0), (1, 1, 1) функция принимает значение 0. Составим соответствующие им дизъюнкты: xÚyÚz, xÚ Ответ: a) СДНФf(x, y, z)= СКНФf(x, y, z)=(xÚyÚz)&(xÚ Упражнение 5.2.Функция f(x1, x2, x3, x4) задана вектором своих значений. Найти СДНФ и СКНФ функции: а) (0010 1010 1110 0110); б) (1100 0011 1010 1011); в) (1001 0110 0010 1001). Решение. а) Указание. Вектор (0010 1010 1110 0110) значений функции f(x1, x2, x3, x4) означает, что f(0, 0, 0, 0)=f(0, 0, 0, 1)=f(0, 0, 1, 1)=f(0, 1, 0, 1)=f(0, 1, 1, 1)=f(1, 0, 1, 1)=f(1, 1, 0, 0)=f(1, 1, 1, 1)=0 и f(0, 0, 1, 0)=f(0, 1, 0, 0)=f(0, 1, 1, 0)=f(1, 0, 0, 0)=f(1, 0, 0, 1)=f(1, 0, 1, 0)=f(1, 1, 0, 1)=f(1, 1, 1, 0)=1. Остальное аналогично решению предыдущего упражнения. Определение 4. Функция f(х1, х2, …, хn) называется суперпозицией функции g(y1, y2, …, ym), h1(х1, х2, …, хn), h2(х1, х2, …, хn), …, hm(х1, х2, …, хn) если f(х1, х2, …, хn)=g(h1(х1, х2, …, хn), h2(х1, х2, …, хn), …, hm(х1, х2, …, хn)). 5.2. Основные классы булевых функций. Во множестве булевых функций выделяют 5 основных классов, играющие большое значение в теории булевых функций. 1. Говорят, что булева функция fсохраняет нуль, если f(0, 0, …, 0)=0. Класс Р0 - класс булевых функций, сохраняющих нуль: Р0={f | f(0, 0, …, 0)=0}. 2. Говорят, что булева функция fсохраняет единицу, если f(1, 1, …, 1)=1. Класс Р1 - класс булевых функций, сохраняющих единицу: Р1={f | f(1, 1, …, 1)=1}. 3. Говорят, что булева функция f является самодвойственной, если она совпадает со своей двойственной. Класс S - класс самодвойственных функций: S={f | f*=f}. 4. Булева функция называется монотонной, если для любых наборов нулей и единиц (a1, a2, …, an) и (b1, b2, …, bn) из условий a1£b1, a2£b2, …, an£bn следует f(a1, a2, …, an)£f(b1, b2, …, bn). Класс М - класс монотонных функций: М={f |(a1£b1, a2£b2, …, an£bn) Þ f(a1, a2, …, an)£f(b1, b2, …, bn)}. 5. Булева функция называется линейной, если она представима в виде линейного многочлена: f(x1, x2, …, xn)=c0Åc1x1Åc2x2Å…Åcnxn. Класс L - класс линейных функций: L={f | f(x1, x2, …, xn)=c0Åc1x1Åc2x2Å…Åcnxn}. Перечисленные выше классы называются классами Поста. Принадлежность функции к классам Поста можно проверить с помощью таблиц истинности. Принадлежность функции к классам Р0 и Р1 проверяется очевидным образом. Принадлежность функции к классу S проверяется так же, как и самодвойственность формулы алгебры логики: по таблице истинности проверяется, что на всех противоположных наборах значений переменных функция принимает противоположные значения (см. ).
Строится помеченный (гипер)куб, в вершинах которого проставляются значения функции. Построив всевозможные маршруты от вершины (0…0) до вершины (1…1), убеждаемся, что на каждом из этих маршрутов при переходе от произвольной вершины (a1, a2, …, an) к смежной вершине (b1, b2, …, bn) будет выполнено условие f(a1, a2, …, an)£f(b1, b2, …, bn). Если для какого-либо маршрута это условие нарушено, то функция монотонной не является. Рассмотрим процедуру проверки на монотонность для функции f(x, y, z)= =x&(yÚz). Построим помеченный куб, в вершинах которого проставлены значения функции f(x, y, z) (рис. 1). Замечаем, что при переходе от вершины к вершине по любому маршруту от (000) до (111), значения функции на вершинах не убывают. Это означает, что функция монотонна. Для функции f(x1, x2, x3, x4)=(x1&x2)®(x3Úx4) от четырёх переменных строим гиперкуб четвёртого порядка (рис.2). Как видим, существует маршрут от вершины (0000) к вершине (1111), для которого при переходе от одной вершины к другой значение функции меняется от 1 к 0. Например, это маршрут ((0000, 1000), (1000, 1100), (1100, 1110), (1110, 1111)). По этому маршруту имеем, что f(1, 0, 0, 0)<f(1, 1, 0, 0).
Проверка принадлежности функции к классу L заключается в том, что сначала находятся значения коэффициентов c0, c1, c2, …, cn в предположении, что функция f линейная. После этого сравниваются таблицы истинности функции f и полученной формулы c0Åc1x1Åc2x2Å…Åcnxn. Коэффициенты находятся из соотношений: c0=f(0, 0, …, 0), c1=c0Åf(1, 0, …, 0), c2=c0Åf(0, 1, …, 0), (5.1) ………………….. cn=c0Åf(0, 0, …, 1). Пример 5.2. Проверим на линейность функции (х&у)Ú( Для функции (х&у)Ú( c0=f(0, 0)=(0&0)Ú( c1=c0Åf(1, 0)=1Å(1&0)Ú( c2=c0Åf(0, 1)=1Å(0&1)Ú( то есть c0Åc1xÅc2у=1ÅxÅу. Сравним таблицы истинности полученной формулы и функции f(х, у)=(х&у)Ú(
Таблицы истинности совпали. Следовательно, f(х, у)=1ÅxÅу и функция f(х, у) является линейной. Для функции х c0=f(0, 0)=0& c1=c0Åf(1, 0)=1Å(1& c2=c0Åf(0, 1)=1Å(0& то есть c0Åc1xÅc2у=1Åу. Сравним таблицы истинности полученной формулы и функции f(х, у)=х&
Как видим, таблицы истинности полученной формулы и функции f(х, у) не совпадают. Следовательно, функция х& Упражнение 5.3. Принадлежат ли функции из упражнений 5.1 и 5.2 к классам Р0, Р1, S, M, L? Решение. а) (из упражнения 5.1) Проверим принадлежность к классам Р0, Р1, S. Имеем f(0, 0, 0)=0 и f(1, 1, 1)¹1. Поэтому f(х, у, z)ÎР0 и f(х, у, z)ÏР1. Далее, f(х, у, z)ÏS. Действительно, имеем, например, f(0, 0, 0)¹ c0=f(0, 0, 0)=0, c1=c0Åf(1, 0, 0)=0Å0=0, c2=c0Åf(0, 1, 0)=0Å1=1, c2=c0Åf(0, 0, 1)=0Å1=1, то есть f(х, у, z)=уÅz. Составим таблицы истинности f(х, у, z) и уÅz:
Таблицы истинности f(х, у, z) и уÅz не совпадают. Следовательно, f(х, у, z) не является линейной, то есть f(х, у, z)ÏL. Другой способ проверки линейности функции основан на так называемых полиномах Жегалкина. Полином Жегалкина. Определение 5. Полиномом Жегалкина называется полином вида
(то есть сумма произведений вида Любая булева функция единственным образом (с точностью до следования слагаемых) представима в виде полинома Жегалкина. Для представления булевой функции в виде полинома Жегалкина достаточно: 1. Привести функцию к ДНФ (КНФ). 2. Выразить операции &, Ú, Ø через операции булева кольца по формулам из п.5.2. Пример 5.3. Найдём полиномы Жегалкина для функций из примера 5.2. Для функции (х&у)Ú( (х&у)Ú( =хуÅ(1Åх)(1Åу)=хуÅ1ÅхÅуÅху=1ÅхÅу, то есть (х&у)Ú( Как видим, для функции х Заметим, что если А и В - различные конституенты единицы, то они содержат хотя бы одну пару противоположных литер, и тогда АВ=0, АÚВ=АÅВ. Поэтому полином Жегалкина удобно получать из СДНФ формулы. Упражнение 5.4. Построить полиномы Жегалкина для функций упражнения 5.1. Решение. а) Имеем СДНФf(x, y, z)=
=zÅхzÅуzÅ хyzÅyÅхyÅyzÅхyzÅxzÅxуz=yÅzÅxyÅхyz. То есть Функциональная полнота. Определение 6. Система булевых функций F={f1, f2, …, fn} называется полной, если любая булева функция представима в виде суперпозиции функций из F. Система булевых функций является полной тогда и только тогда, когда для каждого из классов Поста система содержит функцию, не лежащую в данном классе. Определение 7. Система булевых функций называется базисом, если она полна, и удаление любой функции из этой системы делает её неполной. Упражнение 5.5. Проверить полноту следующих систем булевых функций: а) {®, Ø}; б) {«, Å}; в) {¯}; г) { &, ®}. Решение. а) Принадлежность данных функций к каждому из классов Поста сведём в таблицу:
В таблице знаком «+» на пересечении строки с указанием функции со столбцом с указанием класса обозначен тот факт, что функция принадлежит соответствующему классу, а знаком «-» - тот факт, что функция не принадлежит данному классу. В каждом столбце имеется знак «-», то есть для любого класса Поста система F={®, Ø} содержит функцию, не лежащую в данном классе. Следовательно, система функций F={®, Ø} является полной. Она образует базис, так как удаление любой функции из этой системы ведёт к тому, что оставшаяся система является неполной.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 B. Если (х, y)Îf, то пишут y=f(x) или f: x®y. При этом y называется значением функцииf при значении аргументаx, а также говорят, что функция fставит в соответствие элементу x элемент y.
B. Если (х, y)Îf, то пишут y=f(x) или f: x®y. При этом y называется значением функцииf при значении аргументаx, а также говорят, что функция fставит в соответствие элементу x элемент y. (Ø), &, Ú, ®, «, |, ¯, Å. Но в отличие от формул алгебры логики эквивалентность трансформируется в равенство. Поэтому во всех свойствах логических операций знак «~» меняется на знак «=», и получаем соответствующие свойства логических операций над функциями: f&g=g&f, и т.д.
(Ø), &, Ú, ®, «, |, ¯, Å. Но в отличие от формул алгебры логики эквивалентность трансформируется в равенство. Поэтому во всех свойствах логических операций знак «~» меняется на знак «=», и получаем соответствующие свойства логических операций над функциями: f&g=g&f, и т.д. различных булевых функций, то есть их - конечное число, в то время как формул от п переменных можно рассматривать сколько угодно.
различных булевых функций, то есть их - конечное число, в то время как формул от п переменных можно рассматривать сколько угодно.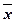
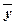 z,
z, 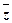 , x
, x  Проверка принадлежности функции к классу М на первый взгляд также очевидна: достаточно по таблице истинности убедиться, что из a1£b1, a2£b2, …, an£bn следует f(a1, a2, …, an)£f(b1, b2, …, bn). Но с ростом числа переменных эта процедура становится достаточно громоздкой. Основная проблема возникает при выделении пар наборов (a1, a2, …, an) и (b1, b2, …, bn) таких, чтобы можно было произвести их сравнение a1£b1, a2£b2, …, an£bn. Тем не менее, при небольшом числе переменных существуют достаточно эффективные процедуры. Опишем одну из процедур для случаев п=3 и п=4. Она заключается в следующем.
Проверка принадлежности функции к классу М на первый взгляд также очевидна: достаточно по таблице истинности убедиться, что из a1£b1, a2£b2, …, an£bn следует f(a1, a2, …, an)£f(b1, b2, …, bn). Но с ростом числа переменных эта процедура становится достаточно громоздкой. Основная проблема возникает при выделении пар наборов (a1, a2, …, an) и (b1, b2, …, bn) таких, чтобы можно было произвести их сравнение a1£b1, a2£b2, …, an£bn. Тем не менее, при небольшом числе переменных существуют достаточно эффективные процедуры. Опишем одну из процедур для случаев п=3 и п=4. Она заключается в следующем.
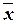 &
& 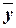 ) и х
) и х  &
& 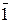 &
& 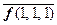 . Принадлежность к классу М проверяется аналогично тому, как это проделано выше. Проверим принадлежность к классу L. Предположим, что функция линейна: f(х, у, z)=c0Åc1xÅc2уÅс3z, где
. Принадлежность к классу М проверяется аналогично тому, как это проделано выше. Проверим принадлежность к классу L. Предположим, что функция линейна: f(х, у, z)=c0Åc1xÅc2уÅс3z, где Åс,
Åс, ), где суммирование ведётся по некоторому множеству различных наборов (i1, i2, …, ik), в которых все ij также различны.
), где суммирование ведётся по некоторому множеству различных наборов (i1, i2, …, ik), в которых все ij также различны.