
|
|
Конъюнктивная нормальная форма. Совершенная конъюнктивная нормальная форма.Определение 5. Дизъюнкция
называется элементарной дизъюнкцией или дизъюнктом. Как и в случае конъюнктов, существует 2n различных элементарных дизюъюнкций от n переменных. При этом значение элементарной дизюъюнкции вида (4.2) равно 0 тогда и только тогда, когда xi=1-si для всех i=1, 2, …, n. Конъюнкция вида (4.1) называется также конституентой нуля. Определение 6. Конъюнктивной нормальной формой формулыА (КНФА) называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций. Пример 4.2. Для формулы А= Как и в случае ДНФ, КНФ формулы неединствен. Их можно составить сколько угодно. К КНФ формулы можно прийти по следующему алгоритму: I шаг: Приведение операций |, ¯, ®, «, Å к операциям &, Ú или их отрицаниям: 1. Если в формуле участвуют операции |, ¯, и Å, то от них с помощью операции отрицания переходим к отрицанию соответственно конъюнкций, дизъюнкций или эквиваленций. 2. Если в формуле участвует операция «, то от неё с помощью закона т) упражнения 3.2 переходим к операции ®. 3. Если в формуле участвует операция ®, то от неё с помощью закона п) упражнения 3.2 преходим к операции Ú. II шаг. Отнесение отрицаний к пропозициональным переменным. 4. Если в формуле участвуют отрицания конъюнкций или дизъюнкций, то с помощью законов де Моргана отрицания приводим к пропозициональным переменным. 5. Если в формуле участвует двойное отрицание, то с помощью закона снятия двойного отрицания они убираются. III шаг. Получение КНФ. С помощью свойства дистрибутивности Ú относительно & все подформулы вида AÚ(B1&B2&…&Bk) приводим к подформулам вида (AÚB1)&(AÚB2)&…&(AÚBk) до тех пор, пока не получим конъюнкцию элементарных дизъюнкций. Таким образом, мы доказали, что любая формула эквивалентна некоторой КНФ. Очевидно, А&А&…&А~А, и поэтому в КНФ элементарная дизъюнкция может повторяться сколько угодно раз. В результате мы приходим к тому, КНФ формулы можно построить сколько угодно. Потребуем, чтобы КНФ удовлетворяла следующим четырём свойствам совершенства: 1. Каждый дизъюнкт КНФ формулы содержит все переменные или их отрицания, входящие в формулу. 2. Все дизъюнкты, входящие в КНФ, различны. 3. Ни один дизъюнкт, из которых состоит КНФ, не содержит одновременно переменную и её отрицание. 4. Ни один дизъюнкт не содержит одну же литеру два и более раз. Определение 7. КНФ формулы, удовлетворяющей всем условиям совершенства, называется совершенной конъюнктивной нормальной формой данной формулы (СКНФ). Для того, чтобы получить СКНФ формулы А, достаточно сначала формулу привести к КНФА, а затем применить к полученной КНФ эквивалентные преобразования следующих видов, позволяющие последовательно получать эквивалентную КНФА, удовлетворяющие всем условиям совершенства: 1. Если в КНФА какой-либо дизъюнкт В не содержит переменную хi или её отрицание, то используя равносильности B~ВÚ(хi& 2. Если в КНФА входят два или более одинаковых дизъюнкта B, то лишние отбрасываем, пользуясь равносильностью B&B&…&B~B. 3. Если некоторый дизъюнкт В, входящий в КНФА, содержит переменную хi и её отрицание 4. Если некоторый дизъюнкт, входящий в КНФА, содержит одну и ту же литеру Упражнение 4.3. С помощью эквивалентных преобразований привести формулы упражнения 3.4 к СКНФ. Решение. з) Приведём формулу к КНФ: (x|
Получили КНФ формулы. Теперь преобразуем КНФ по алгоритму получения всех условий совершенства:
á(1) Одновременно заменили | на отрицание операции &,и ® - на отрицание Ú. (2) Одновременно применили закон двойного отрицания и Å заменили на « и его отрицание. (3) Операцию « заменили на ®. (4) Применили закон де Моргана. (5) Заменили ® на Ú. (6), (7) Одновременно применили законы де Моргана и снятия двойного отрицания. (8) Воспользовались ассоциативностью и коммутативностью Ú. (9) 1-й и 2-й конъюнкты объединили в один с помощью дистрибутивности & относительно Ú. (10) К подформуле (11) Воспользовались тем, что (12) Применили сложную дизъюнкцию относительно Ú. (13) Применили законы исключённого третьего и идемпотентности. (14) В 1-й и 2-й дизъюнкты добавили недостающие литеры и разбили их по два дизъюнкта каждую (1-я операция приведения к СКНФ). (15) Операцию, аналогичную (14) проделали с 3-м и 4-м дизъюнктами. (16) Опустили лишние дизъюнкты. СДНФ формулы существует и единственна. Существование СКНФ для любой формулы вытекает из алгоритма её построения. Другой способ построения СКНФА основывается на следующей эквиваленции: A(х1, х2, …, хn)~ Другими словами, формула A(х1, х2, …, хn) в своей СДНФ содержит те и только те конъюнкты вида (4.2), значения которых равны 0 при xi=1-si для всех i=1, 2, …, n. Например, для формулы А= Таким образом, СКНФA(х1, х2, …, хn)= Упражнение 4.4. С помощью таблиц истинности привести формулы упражнения 3.4 к СКНФ. Решение. д). 1. Составим таблицу истинности формулы (она у нас уже составлена, см. решение задачи д) упражнения 4.2): 2. Выберем те наборы значений переменных, при которых формула принимает значение 0: (0, 0, 1), (0, 1, 1). 3. Составим соответствующие им дизъюнкты: xÚyÚ 4. Составим из них КНФ: (xÚyÚ Ответ: д) СКНФA=(xÚyÚ 4.3. Принцип двойственности. Операция & называется двойственнойк Ú, Ú - двойственной к &. Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания. Определение 8. Формула A* называется двойственной кА, если A* получается из A заменой в ней каждой операции на двойственную. Очевидно, если A* - двойственна к A, то A - двойственна к A*. Поэтому говорят о взаимно двойственных формулах. Очевидно также, что если формулы А и В равносильны, то равносильны и двойственные им А* и В*. Кроме того, если A*(х1, х2, …, хп) - двойственна к A(х1, х2, …, хп), то Определение 9. Формула А называется самодвойственной, если A*~A. Из определения следует, что формула A самодвойственна, если при замене 0 на 1, и 1 на 0 её таблица истинности не меняется (естественно, меняются между собой только строки). Очевидно, формула самодвойственна тогда и только тогда, когда на всех противоположных значениях переменных формула принимает противоположные значения.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
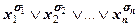 (4.2)
(4.2)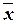 ®(
®( 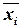 )~ ~(ВÚхi)&(BÚ
)~ ~(ВÚхi)&(BÚ 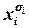 дважды или более, то, пользуясь равносильностью
дважды или более, то, пользуясь равносильностью  )®(zÅ
)®(zÅ  )
) 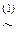 (
(  )Ú(zÅ
)Ú(zÅ  (x&
(x& 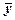 )Ú
)Ú 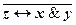
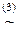
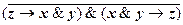
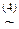 (x&
(x& 
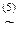
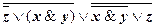
 (x&
(x& 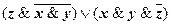
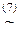
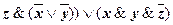
 (x&
(x&  )
) 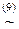
 ))Ú
))Ú  )
) 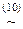 (x&((
(x&((  ))Ú
))Ú 
 (xÚz)&
(xÚz)& 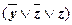 &
& 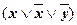 &
& 

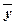 &
& 
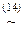
 &
& 
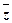 )&
)&  &
& 
 .
.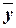 ,
,  ~A*(х1, х2, …, хп). Отсюда следует, что таблица истинности формулы A*, двойственной к А, получается из таблицы истинности А заменой всех 0 на 1 и всех 1 на 0.
~A*(х1, х2, …, хп). Отсюда следует, что таблица истинности формулы A*, двойственной к А, получается из таблицы истинности А заменой всех 0 на 1 и всех 1 на 0.