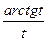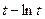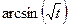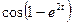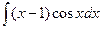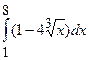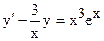|
|
Формулы длин дуг плоских кривых.
вычисляется по формуле:
Пример 8.Найти длину дуги кривой Решение. Кривая симметрична относительно оси Ox. Найдем длину верхней ветви кривой. Из уравнения
Контрольные вопросы. 1.Определённый интеграл 2.Формула Ньютона- Лейбница. 3. Вычисление объёмов тел вращения.
Задания. 1. Вычислить интегралы 1) 5) 2. Найти площади фигур ограниченных линиями: 1) 3.Найти объём тела , образованного вращением фигуры ограниченной линиями: 1) вокруг оси Ox; 2) вокруг оси Oy.
4. Найти длину дуги кривой: а) б) в) Кардиоиды Тема 16. Несобственные интегралы.
Если предел существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует, то интеграл называется расходящимся.
Пример 1. Исследовать сходимость интеграла Решение. 1) Если
2) Если
Итак, данный интеграл при Пример 2.Исследовать сходимость Решение.Сравним подынтегральную функцию
Но интеграл
Пример 3.Исследовать сходимость Решение. 1) Если
2) Если
3) Если
Контрольные вопросы. 1. Несобственные интегралы. 2. Признак сравнения. Задания. 1. Вычислить интегралы 1)
2.Исследовать сходимость интегралов 1) 4) Контрольная работа № 1 Задание № 1. Найти производную функций: Вариант 1: а) y=(5x2+4 в) y=2tg x ∙sin3x, г) y=ln ctg Вариант 2: а) y=(2x4 – в) y=3sin2x ∙arccos x, г) y= ln tg 4x. Вариант 3: а) y=( в) y=2arctg x ∙sin3x, г) y= ctg ln Вариант 4: а) y=( в) y=3cos3x ∙sin3x, г) y= tg ln 4x. Вариант 5: а) y=(3x7+5 в) y=2arcsin x ∙tg x, г) y= ln Вариант 6: a) y= (5x4 – в) y=5tg2x ∙arccos x, г) y= ln Вариант 7: а) y= (4x3 + в) y=e arctg x ∙cos 3x, г) y=ln Вариант 8: а) y= (7x5–3 в) y=5arccos 2x∙∙sin x, г) y=sin( ln5x). Вариант 9: а) y= (3x4 + в) y=2cos x ∙arcsin x, г) y=ln sin 5x. Вариант 10: а) y= (6x3 – в) y=5 tg2x ∙arctg2x, г) y=ln cos 2x.
Задание № 2.
Найти пределы функций: Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Задание № 3.
Провести полное исследование функции и построить ее график:
Вариант 1: Вариант 3: Вариант 5: Вариант 7: Вариант 9: Задание №4 . Найти производную параметрически:
Задание №5.Найти производную
Задание №6. а) вычислите определенный интеграл b) найдите первообразную и сделайте проверку дифференцированием.
Задание №7. Найдите частные решения дифференциальных уравнений.
Рекомендуемая литература
1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М., 1989. 2. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Ч. 1. – М., 1982. 3. Мантуров О.В., Матвеев Н.М. Курс высшей математики. – М., 1986. 4. Данко П. Е..и др. Высшая математика в примерах и задачах. – М.: Высшая математика, 1986. 5. Богомолов Н.В. Практические занятия по математике. – М., 1983. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
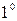 Длина
Длина  кривой, заданной уравнением
кривой, заданной уравнением  ,
,  вычисляется по формуле:
вычисляется по формуле:
 Длина
Длина 
 , вычисляется по формуле:
, вычисляется по формуле:
 Длина
Длина 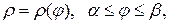
 .
. от
от  до
до 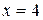 .
. . По формуле вычисления длины дуги получим
. По формуле вычисления длины дуги получим

 ; 2)
; 2)  3)
3) 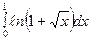 ; 4)
; 4) 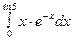 ;
; : 6)
: 6)  .
. ,
,  ,
,  ; 2)
; 2)  , у=1-х2, х=0; 3)
, у=1-х2, х=0; 3)  , х=е ,у=0.
, х=е ,у=0.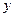 =4-х2; у=0; х=0;
=4-х2; у=0; х=0; 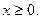
 отсеченной осью Ox;
отсеченной осью Ox;

 Несобственные интегралы первого рода с бесконечными пределами определяются как интегралы вида:
Несобственные интегралы первого рода с бесконечными пределами определяются как интегралы вида: ,
,  ,
, 
 Если
Если  непрерывна для всех значений отрезка
непрерывна для всех значений отрезка  , кроме точки с, в которой
, кроме точки с, в которой 
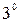 Признак сравнения. Если функции
Признак сравнения. Если функции  непрерывны на промежутке
непрерывны на промежутке  и удовлетворяют на этом промежутке условию
и удовлетворяют на этом промежутке условию  , то из сходимости интеграла
, то из сходимости интеграла 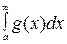 следует сходимость интеграла
следует сходимость интеграла  , и из расходимости интеграла
, и из расходимости интеграла 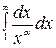 , где
, где  - некоторое число.
- некоторое число. , то для любого
, то для любого 
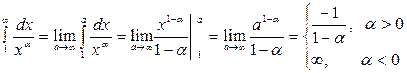
 , то для любого
, то для любого  .
. сходится, при
сходится, при 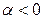 расходится и при
расходится и при  расходится.
расходится. .
. с функцией
с функцией  на
на  . Очевидно, что
. Очевидно, что .
. сходится, так как
сходится, так как  (см. пример 1.) Следовательно, согласно признаку сравнения , сходится и данный ряд.
(см. пример 1.) Следовательно, согласно признаку сравнения , сходится и данный ряд. , где
, где 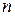 - некоторое число.
- некоторое число. , для некоторого
, для некоторого  ,то
,то
 , то
, то ,
, , для некоторого
, для некоторого  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 

 , 2)
, 2)  3)
3) 
 , 5)
, 5)  , 6)
, 6)  .
. + 6)5, б) y=
+ 6)5, б) y=  ,
, .
.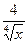 +2)3, б) y=
+2)3, б) y= 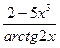 ,
, x8+8
x8+8  –1)3, б) y=
–1)3, б) y=  ,
, .
. x5–3
x5–3  – 4)5, б) y=
– 4)5, б) y=  ,
, –3)3, б) y=
–3)3, б) y=  ,
, .
. +3)2, б) y=
+3)2, б) y=  ,
, .
. -2)5, б) y=
-2)5, б) y=  ,
,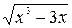 .
. - 5)4, б) y=
- 5)4, б) y=  ,
, -3)5, б) y=
-3)5, б) y=  ,
, + 6)5, б) y=
+ 6)5, б) y=  ,
, ;
;  ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
;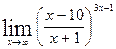 ;
;  .
. ;
;  ;
;  ;
; ;
;  .
. ;
;  ;
; 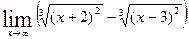 ;
;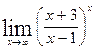 ;
;  .
. ;
;  ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
; ;
; 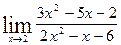 .
. ;
;  ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
; ;
;  .
. . Вариант 2:
. Вариант 2:  .
. . Вариант 4:
. Вариант 4:  .
. . Вариант 6:
. Вариант 6:  .
. . Вариант 8:
. Вариант 8:  .
. . Вариант 10:
. Вариант 10:  .
. функции, заданной
функции, заданной .
.